2021中青杯数学建模竞赛思路(更新)

Posted 2021-06-06 微信公众号：您好啊数模君

A题:汽车组装车间流水线物料配送问题

 

图中各道路节点已知，但具体仓库点(装货点)和工位位置(卸货点)，就设置个大概的等间距通过linspace函数划分取数

 

这道题问题都很常规，但需要构建有向矩阵来算路径距离，有向矩阵构建规则自己写，写不来就挨个手打出来

 

构建程序见群322273643群文件，记得将各点编号，方便之后调用

第一问承包就是打包，但是这个打包方式不同，需要结合最短路径来做，小车都是从B点开始，执行完任务都会返回B点，要到达一个工位上的路径需要从B点开始，到达对应编号的仓库，在到达对应工位，这里注意区分下装配一区和二区的道路分布，一区和二区各24各点求得在最短路径距离，按距离进行打包(当然也可以在此基础上，再考虑下各工位之间的距离，觉得麻烦可以不考虑)，仅考虑B点到工位的距离，就是一维数据聚类，考虑各工位之间的距离就是二维数据聚类(聚类算法可以是k-means、FCM或其他方法)；除了聚类也可以自写一个启发式算法(推荐使用模拟退火框架)，各工位依次通过randi函数随机10以内的整数，当某个整数累计5次数，则排除该整数，同一整数的对应为一个小车的承包工位，将打包的几个点看作是一辆小车需要经过的地点，求一个最短距离，目标函数就是距离之和最小。第一问不管使用启发式算法做还是直接聚类做，最好是给一个总的路径距离。

第二问，工厂里则是会按排班表来规划拖车的工作，先看下第三问，要求不能停线，那么第二问就是可以停线，但是尽可能保证停线时间更短，结合第一问，第二问为多目标优化问题，第一个目标函数为拖车总数，第二个目标函数为总停线时间，在本问，小车默认走最短路径完成装卸任务，第二问就不用考虑最短路径长度了。上文知道了各点之间的有向距离，这里有车速那么就可以计算得到装卸过程的时间。第二问没有规定具体工位的需求时间，给的图二图三只是个参考，就自行设置初始各工位的工作时间状态以及需求时间，外循环为优化寻优，内循环为蒙特卡洛模拟，比如内循环模拟2小时，取后一个小时的数据来计算该段时间内的目标函数值。本问的拖车数在蒙塔卡罗模拟时不做限制，但肯定用不了10个，时刻记录在用拖车数的变化就行，最后取最大拖车数作为目标函数，本问的降本就体现在拖车数上。本问在模拟的时候判断是否发车的条件，通过第一问可以知道B点装货到每个工位的路径长度，通过速度能计算得到行程时间，同时每个工位也设置了相应的需求时间，也就是需要多久补充一次原料，可以用数组时刻记录各工位的剩余时间，设定一个临界值，当有工位时间低于该临界值时，立即发车，可以参考第一问的承包区不超过5个工位的条件，这时系统自动计算剩余时间最少的5个工位，派出小车从B点出发先到各个仓库点装货再到各个工位去。路径默认最短路径，因此该模拟过程还需要设计一个最短路径算法，尽可能简单，不然程序运算效率很低，先通过Dijk和Floud算法根据有向矩阵求出任意两点间最短距离备用，发车可看作两个最短路径，一个是装货路径，一个是从装货结束点到所有工位的路径，分别求最短路径，因为经过的只有几个点，直接随机模拟几次选最总路程最短的即可。

第三问不允许停线，那么就第二问删除拖车数这一目标函数进行寻优，最后与第二问做对比

 

B题：港珠澳大桥桥梁设计与安全策略

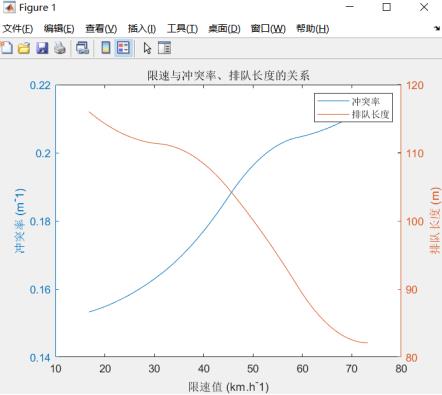
车道模拟，汽车安全可以用冲突率(比如模拟的追尾次数占总通行的车辆数）、排队长度(反映拥堵情况)和道路车辆速度均方差来体现，一般冲突率与排队长度得关系如下：

 

第一问是安全行驶速度设计问题，和闸道限速设计差不多，转向车道可以看作是闸道。如果要用vissim软件仿真按如下模型建立即可，设置记录数据时间间隔等参数，最后导出车辆状态数据文件做分析。

 

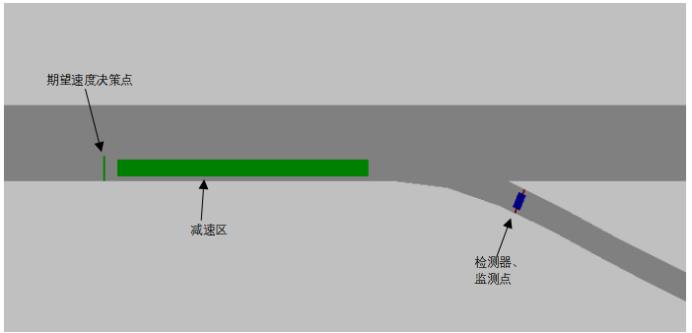
模型和车辆跨线也很类似，都是提前减速、转弯

 

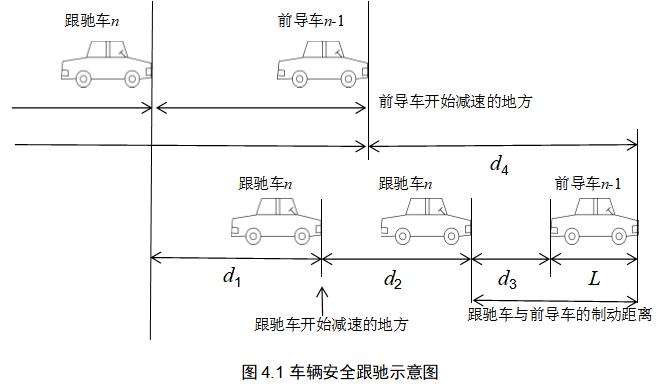
除了转弯部分，还有个比较重要的就是车辆跟驰，模型中安全距离也是必不可少的

 

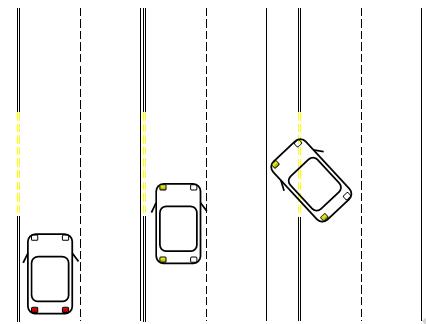
是否超车，向左还是向右超车，也都是需要根据车辆的前后左右是否有车辆行驶

车道产生拥堵是因为前方车辆速度较慢，而后方车辆以较高速度驶来，道路模拟中每辆车的车速也不都是不变的，除了小型车还有大型车，大型车的车速和加速度均小于小型车。

具体模型就不细说，分享两个案例程序（群322273643）里面有。

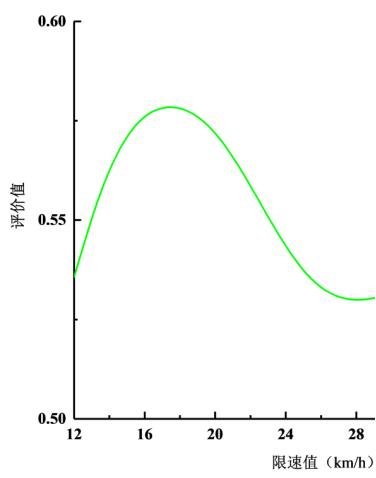
车道模拟程序运算时间较长，就不推荐使用优化算法了，设计不同的速度范围计算出冲突率、排队长度、道路车辆速度均方差等指标，最后评估出最大安全行驶速度，可以评价算法量化不同弯道限速下的安全水平或者危险水平，速度不应太慢也不应太快，下图为安全水平的评价值

 

模型除了将不同风速不同限速下的冲突率和排队长度展示出来，还可以绘制下某段路程某段时间的交通流图，下面上图就比右图通畅，下图展现了拥堵情况。

 

 

第二问研究大桥主体，那就只分析主车道，车道数自行设置，第二问说到的台风影响，横向风速主要影响汽车偏移，纵向主要影响影响车速。我们物理中也学过车为什么设计为拱线形，车开得越快，气流对车向上的作用力越大，因此如果车速过快，在大风天气更容易出事故。再看第三问要求的是对通行能力的研究，因此这道题的侧重点不是复杂的物理分析，如果要分析翻不翻车，那就还得考虑车外形，没有大型仿真软件是做不了的。车速对应的风速级别如下：

 

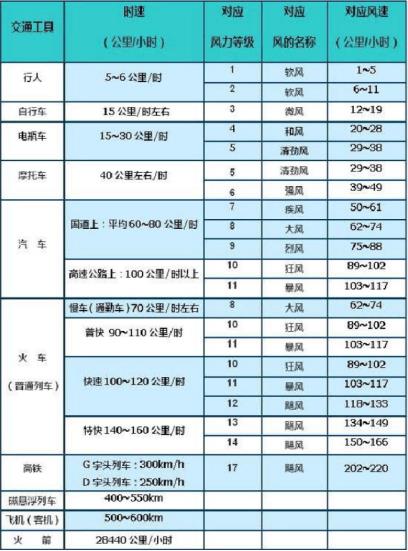
单位面积上车辆所承受的压力可通过P=ρv＾2/2公式(单位面积上所承受压力的大小，ρ为空密度1.29)计算，在乘以车辆底部面积(分大小车辆设置)即可，这里的v应当为风速和车速的向量和，桥梁所在的是沿海区域，对于桥面行驶的车辆来说主要是横向风。车辆在桥面上最大安全行驶速度应当保证P*S底部面积要小于车辆重量，因此可以通过该公式计算最大限制速度，但这速度仅是车辆不被掀翻的层面，还得考虑冲突率、排队长度、道路车辆速度均方差等指标分析出合理的安全速度。台风级别除了对最大限制速度的影响，还对加速度有一定的影响，可以现确定下摩擦力参数，例如一台车2000kg，G=20000N，无风情况下正常行驶60km/s，加速度5m/s^2，根据P=ρv＾2/2公式算的此刻车向下合力为18200N左右，加速度5m/s^2下的向前合力为10000，那么摩擦系数就为0.55左右，一般路面摩擦系数在0.4-0.6之间，自己根据你所研究的车辆设置一个摩擦系数即可，那么受风速影响的加速度公式也就推出来了。有了这些参数，就可以进行模拟了，不同台风级别情况下可以计算得到最大限制速度和加速度，再次基础上，在最大限制速度范围内等间距分别取速度带入第一问程序进行模拟，取安全水平最好的速度作为最大安全速度，最后拟合不同台风级别与对应最大安全速度的关系曲线。

第三问选择一种台风级别进行模拟，上文已经谈到了安全、气候，交通事故处理和交通控制可以选择性考虑，交通事故处理就比如模拟过程中突发哪条路段不能同行，车辆必须提前变道，这样会造成拥堵，交通控制就比如说，在进口处进行交通管制，控制车流量，或者是大货车比例，以减少桥上的拥堵。车辆较多的情况，车辆变道、超车等因素会造成一定的拥堵，短时间无法调节，可能会造成一段时间的拥堵。因此本问可以在不同交通流量及允许大货车的比例上进行研究，给出一个合理的方案。