DataStruct # 线性表

Posted 2021-06-06 LRcoding

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了DataStruct # 线性表相关的知识，希望对你有一定的参考价值。

3. 线性表

零个或多个数据元素的有限序列

3.1 线性表的定义

首先它是一个序列，也就是说元素是有顺序的，然后它的个数是有限的

线性表

a1（第一个元素）没有前驱， an（最后一个元素）没有后继。其他元素有且只有一个直接前驱，一个直接后继。

所以线性表元素的个数 n （n >= 0）定义为线性表的长度，n = 0时，称为空表

线性表中的数据元素，要求是相同的类型，可以是基本类型，也可以为引用类型等。

3.2 线性表的抽象数据类型

ADT 线性表（List）
Data
    数据对象集合为{a1, a2, ..., an}，每个元素的类型相同，关系为一对一的关系。第一个元素没有前驱，最后一个元素没有后继，其他元素【有且仅有】一个直接前驱，一个直接后继。
Operation
    InitList (*L);          // 初始化操作，建立一个空的线性表
    ListEmpty (L);          // 若线性表为空，返回true，否则返回false
    ClearList (*L);         // 清空线性表
    GetElem (L, i, *e);     // 将线性表 L 中第 i 个位置元素返回给 e
    LocateElem (L, e);      // 在线性表 L 中查找与给定值 e 相等的元素。
                            // 查找成功返回元素在表中的序号，否则返回 0
    ListInsert (*L, i, e);  // 在线性表 L 中第 i 个位置，插入新元素 e
    ListDelete (*L, i, *e); // 删除线性表 L 中第 i 个位置元素，用 e 返回其值
    ListLength (L);         // 返回线性表 L 的元素个数
endADT

上述操作都是最基本的，要进行复杂操作的话，可以使用这些基本操作的组合来实现。

3.3 线性表的顺序存储结构

3.3.1 顺序存储定义

用一段地址连续的存储单元依次存储线性表的数据元素。

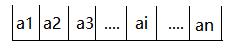
3.3.2 顺序存储方式

在内存中找个地方，通过类似于图书馆占位的形式，把一定内存空间给占了，然后把相同数据类型的数据元素依次存放在这块空地中。

通常使用一维数组来实现顺序存储结构。将第一个数据元素存到数组下标为 0 的位置，接着把线性表相邻的元素存储在数组中相邻的位置。

#define MAXSIZE 20             // 存储空间初始分配量
typedef int ElemType;          // typedef 为C语言中 起别名 的关键字
typedef struct {
    ElemType data[MAXSIZE];    // 数组存储数据元素，最大值为MAXSIZE
    int length;                // 线性表当前长度
} SqList;

通过上面的结构代码，我们可以知道，描述顺序存储结构需要三个特性：

存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置
线性表的最大存储容量：数组长度 MAXSIZE
线性表的当前长度：length

在初始化线性表的时候，虽然申请了 MAXSIZE 个位置，不一定全部用上，但一定不能超过这个值。

注意：数组的长度是存放线性表的存储空间的长度，一般是不变的（也可以动态分配数组），线性表的长度是线性表中数据元素的个数，随着插入和删除的操作，这个值是变化的。在任意时刻，线性表的长度 <= 数组的长度

3.3.3 地址计算方法

由于线性表的起始是从 1 开始，而数组的下标是从 0 开始的，所以线性表的第 i 个元素要存储在数组下标为 i - 1 的位置。即：

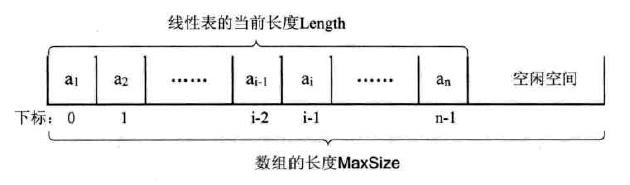
所以在分配数组空间时要 >= 当前线性表的长度

其实，存储器中的每个存储单元都有自己的编号，这个编号称为地址。

第 i 个数据元素 ai 的地址的计算公式：LOC(ai) = LOC(a1) + (i - 1) * c

LOC表示获得存储位置的函数
c 表示每个数据元素占用的存储单元大小
i 表示第几个元素

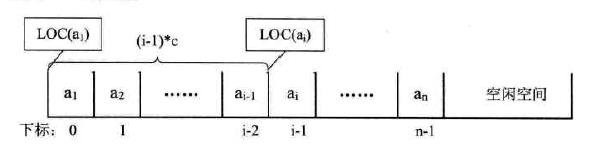
通过这个公式，我们可以随时算出线性表中任意位置的地址，那么对线性表位置的存入或取出数据，都是一样的时间，也就是一个常数，则时间复杂度为 O(1)，这种存储结构一般称为随机存取结构。

3.4 顺序存储结构的插入与删除

3.4.1 获得元素操作

思路：

想要获得第 i 个元素的值，那么返回数组下标为 i - 1 位置的值即可

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef int Status;
Status GetElem(SqList L, int i, ElemType *e) {
    if(L.length == 0 || i < 1 || i > L.length) {
        return ERROR;
    }
    *e = L.data[i - 1];
    return OK;
}

3.4.2 插入操作

思路：

插入位置不合理，抛出异常
若线性表长度已经等于了数组长度，则抛出异常或者动态增加容量
从最后一个元素开始向前遍历到第 i 个位置，将它们挨着后移一位
将要插入元素填入 i 位置处
表的长度 + 1

Status ListInsert(SqList *L, int i, ElemType e) {
    if (L->length == MAXSIZE) {
        return ERROR;
    }
    if (i < 1 || i > L->length + 1) {
        return ERROR;
    }
    if (i <= L->length) {
        int j;
        // 元素后移，从后开始移
        for(j = L->length - 1; j >= i - 1; j--) {
            L->data[j + 1] = L->data[j];
        }
    }
    L->data[i - 1] = e;
    L->length++;
    return OK;
}

3.4.3 删除操作

思路：

如果删除位置不合理，抛出异常
取出删除元素
删除位置后面的元素前移一步
线性表的长度 - 1

Status ListDelete(SqList *L, int i, ElemType *e) {
    if (L->length == 0) {
        return ERROR;
    }
    if (i > L->length || i < 1) {
        return ERROR;
    }
    if (i < L->length) {
        *e = L->data[i - 1];
        int j;
        for(j = i; j < L->length; j++) {
            L->data[j - 1] = L->data[j];
        }
    }
    L->length--;
    return OK;
}

3.4.4 线性表顺序存储结构的优缺点

在存储、读取数据时，因为有地址计算公式的存在，可以精确定位地址，所以时间复杂度都为O（1）

在插入和删除数据时，最好的情况都是操作最后一个位置的元素，无需移动其他元素，此时的时间复杂度为O（1），最坏的情况是操作第一个位置的元素，需要移动 n - 1 个元素，时间复杂度为O（n），所以总体时间复杂度就是O（n）

优点：
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间（一对一的关系）
- 可以快速地存取表中任一位置的元素
缺点：
- 插入和删除操作需要移动大量元素
- 当线性表长度变化较大时，难以确定存储空间的容量
- 造成存储空间的“碎片”

3.5 线性表的链式存储结构

解决顺序存储结构插入和删除元素时，需要移动大量元素的问题。

可以把数据元素存储在内存中的任意位置，只需要让第一个元素知道第二个元素的位置（内存地址）在哪，然后找到它，第二个知道第三个的地址。。。。。

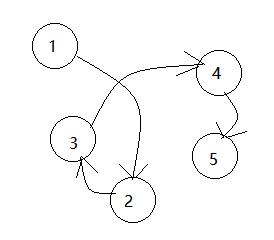
3.5.1 线性表链式存储结构定义

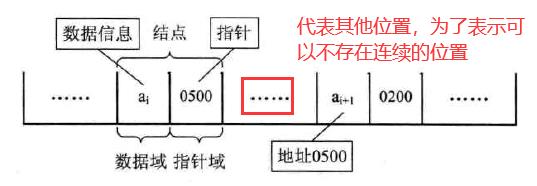
用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以不连续。然后每个数据元素除了存储数据元素信息，还需要存储后继元素的存储地址。

将存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。数据域和指针域组成数据元素 ai 的存储映像，称为结点（Node）。

n 个结点链成一个链表，即为线性表的链式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表。

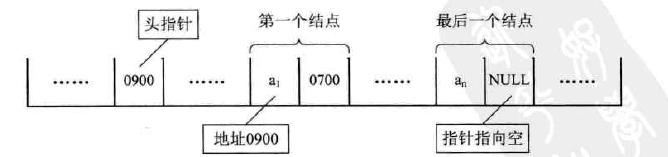
单链表中第一个结点的存储位置叫做头指针，指向第一个结点，整个链表的存取必须是从头指针开始进行。最后一个结点，因为没有后继了，所以它的指针为“空”（用 NULL 或者 ^ 表示）

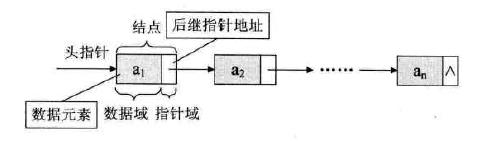
更加直观的图：

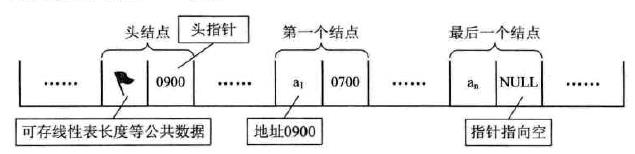
为了统一形式，更加方便对链表进行操作，在单链表的第一个结点前面附加一个结点，称为头结点。头结点的数据域里面可以不存信息，指针域存储指向第一个结点的指针。

更加直观的图：

3.5.2 头指针与头结点的区别

头指针：
- 链表指向第一个结点的指针，如果链表有头结点，则是指向头结点的指针
- 头指针具有标识作用，所以常用头指针冠以链表的名字
- 不论链表是否为空，头指针均不为空
头结点：
- 为了操作的统一和方便而设立的，放在第一个结点之前
- 头结点的数据域一般无数据，也可存放链表的长度
- 有了头结点，对第一个元素的操作就与其他结点的操作就统一了
- 头结点不一定需要

3.5.3 线性表链式存储结构代码描述

typedef struct Node {
    ElemType data;
    struct Node *next;
} Node;
typedef struct Node *LinkList;

从代码中我们可以知道，结点 Node 由数据域（存放数据元素）和指针域（存放后继结点地址）组成。

假设 p 是指向线性表中第 i 个元素的指针，那么该结点 ai 的数据域： p->data 来表示，它的值是一个数据元素。指针域用： p->next 来表示，它的值是一个指针，指向第 i + 1 个元素。

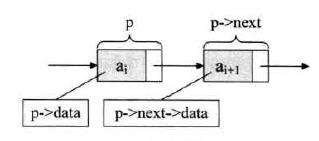
3.6 单链表的读取

由于现在没法直接计算元素的存储地址，所以对于线性表的链式存储结构，要取到一个数相对麻烦一些。

思路：

声明一个结点 p 指向链表的第一个节点，初始化 j 从 1 开始
当 j < i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个节点，j++
若到链表末尾 p 为空，则说明第 i 个元素不存在
否则查找成功，返回结点 p 的数据

Status GetElem(LinkList L, int i, ElemType *e) {
    LinkList p = L->next;  // 声明一个结点 p，并让它指向链表 L 的第一个结点
    int j = 1; // 计数器
    while (p && j < i) { // p不为空或者 j 还没有等于 i 的时候，循环继续
        p = p->next; // 让 p 指向下一个结点
        j++;
    }
    if (!p || j > i) {
        return ERROR;
    }
    *e = p->data;
    return OK;
}

对于链式存储结构来说，找一个元素就是从头开始找，直到第 i 个元素位置。所以最好的情况是O（1），最坏的是O（n）

因为链表没有定义表长，所以不知道要循环多少次，需要使用 while 循环

3.7 单链表的插入与删除

3.7.1 单链表的插入

要在 p 和 p->next 中间插入一个结点，无需改动其他的，只需要改指针的指向即可。

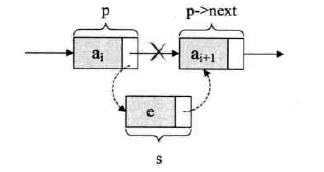
先将结点 s 的指针指向结点 p->next，记录下插入后，后继结点的地址，然后将 p 的指针域指向 s 即可。

思路：

声明一结点 p 指向链表的第一个结点，初始化 j 从 1 开始
当 j < i 时，遍历链表，让 p 的指针向后移动，不断指向下一个结点，j++
若到了链表末尾 p 为空，则说明第 i 个元素不存在
否则查找成功，在系统中生成一个空结点 s
将数据元素 e 赋值给 s->data
单链表的标准插入语句：s->next = p->next; p->next = s;

Status ListInsert(LinkList *L, int i, ElemType e) {
    int j = 1;
    LinkList p, s;
    p = *L;
    while(p && j < i) {
        p = p->next;
        j++;
    }
    if(!p || j > i) {
        return ERROR;
    }
    s = (LinkList)malloc(sizeof(Node)); // 生成新结点(C标准函数)
    s->data = e;
    s->next = p->next;
    p->next = s;
    return OK;
}

3.7.2 单链表的删除

删除相对简单，只需要将 p->next 指向删除结点的下一个结点的地址即可；

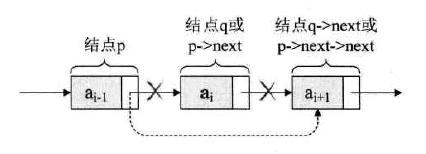
思路：

声明一结点 p 指向链表第一个结点，初始化 j 从 1 开始
当 j < i 时，遍历链表，让 p 的指针向后移动，不断指向下一个结点， j++
若到链表 p 为空，则代表第 i 个元素不存在
否则查找成功，将要删除的结点 p->next 赋值给 q
单链表的标准删除语句：p->next = q->next
将 q 结点的数据赋值给 e，作为返回
释放 q 结点

Status ListDelete(LinkList *L, int i, ElemType *e) {
    int j = 1;
    LinkList p, q;
    p = *L;
    while(p->next && j < i) {
        p = p->next;
        j++;
    }
    if(!(p->next) || j > i) {
        return ERROR;
    }
    q = p-next;
    p->next = q->next;
    *e = q->data;
    free(q);  // 让系统回收此结点，释放内存
    return OK;
}

对于插入或删除数据越频繁的操作，单链表的效率就越明显

3.8 单链表的整表创建 – 头插法

对于链表来说，它所占用空间的大小和位置是不需要预先分配划定的，可以根据系统的情况和实际的需求即时生成。

创建单链表的过程就是一个动态生成链表的过程，即从“空表”的初始状态起，依次建立各元素结点，并逐个插入链表。

思路：

声明一结点 p 和计数器 i
初始化一空链表 L
让 L 的头结点的指针指向 NULL，即建立一个带头结点的单链表
循环：
- 生成一个新结点赋值给 p
- 随机生成一数字赋值给 p 的数据域 p->data
- 将 p 插入到头结点与前一个新结点之间（头插法）

void CreateListHead(LinkList *L, int n) {
    LinkList p;
    int i;
    srand(time(0));  // 初始化随机数种子
    *L = (LinkList)malloc(sizeof(Node)); // 初始化一个空链表 L
    (*L)->next = NULL; // 建立头结点
    for(i = 0; i < n; i++) {
        p = (LinkList)malloc(sizeof(Node)); // 新结点
        p->data = rand() % 100 + 1;
        p->next = (*L)->next;
        (*L)->next = p;
    }
}

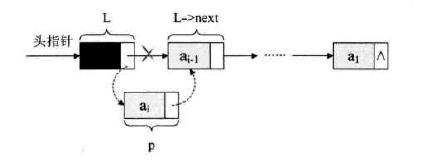
3.9 单链表的整表创建 – 尾插法

与头插法相比，其他思路类似，只是在插入结点时，将新结点插在终端结点的后面。

void CreateListTail(LinkList *L, int n) {
    LinkList p, r;
    int i;
    srand(time(0));
    *L = (LinkList)malloc(sizeof(Node));
    r = *L;  // r为指向尾部的结点
    for(i = 0; i < n; i++) {
        p = (Node *)malloc(sizeof(Node));
        p->data = rand() % 100 + 1;
        r->next = p; // 将表尾终端结点的指针指向新结点
        r = p; // 将当前的新结点定义为表尾终端结点
    }
    r->next = NULL;
}

L 指的是整个单链表，r 是指向尾结点的变量

3.10 单链表的整表删除

思路：

声明一结点 p 和 q
将第一个结点赋值给 p
循环：
- 将下一结点赋值给 q
- 释放 p
- 将 q 赋值给 p

Status ClearList(LinkList *L) {
    LinkList p, q;
    p = (*L)->next;
    while(p) {
        q = p->next;
        free(p);
        p = q;
    }
    (*L)->next = NULL; // 头结点指针域为空
    return OK;
}

3.11 单链表结构与顺序存储结构优缺点

	存储分配方式	时间性能	空间性能
顺序存储结构	一段连续的存储单元依次存储线性表的数据元素	查找：O(1) 插入和删除：O(n)	需要预先分配存储空间
单链表结构	链式存储结构，用一组任意的存储单元存放元素	查找：O(n) 插入和删除：O(1)	不需要分配存储空间，元素个数也不受限制

如果线性表需要频繁的查找，很少使用插入和删除：顺序存储结构

若需要频繁的插入和删除：单链表结构

3.12 静态链表

用数组描述的链表，给没有指针的语言提供的链表设计思路。

让数组的元素都是由两个数据域组成，data 和 cur。也就是说，数组的每个下标都对应一个 data 和一个 cur。数据域 data，用来存放数据元素，而游标 cur 相当于单链表中的 next 指针。

插入和删除时，和单链表结构操作类似的，只需要修改游标的值即可

初始化空的静态链表

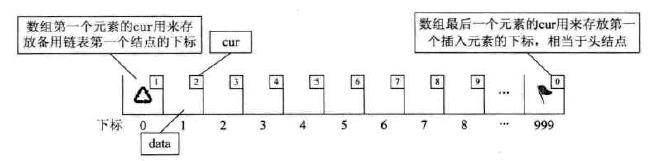
存储数据

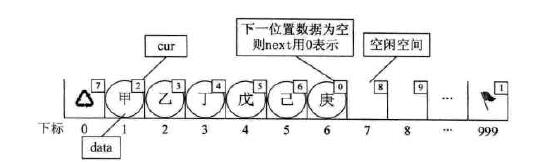
插入数据

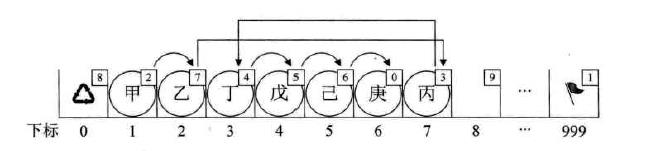
删除数据

3.13 循环链表

将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表

解决的麻烦：从链表中间一个结点出发，访问到链表的全部结点

非空的循环链表：

此时判断循环结束，就由之前的判断 p->next 是否为空，改为了 p->next 是否等于头结点

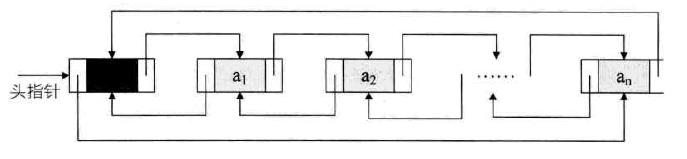
具有尾指针的循环链表：

此时查找开始结点和终端结点的时间复杂度都为 O(1) 了

3.14 双向链表

在单链表的每个结点中，再设置一个指向其前驱结点的指针域。所以在双向链表中的结点，都有两个指针域，一个指向直接后继，一个指向直接前驱。

typedef struct DuLNode{
    ElemType data;
    struct DuLNode *prior;  // 直接前驱指针
    struct DuLNode *next;
} DuLNode, *DuLinkList;

插入操作：

假设存储元素 e 的结点为 s，要实现将结点 s 插入到结点 p 和 p->next之间，需要先用s的前驱和后继分别记住p和p->next的地址

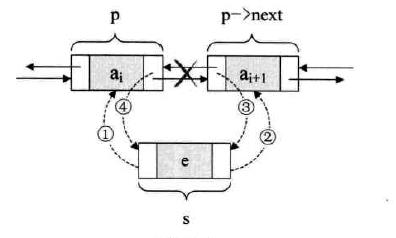
// ① 把 p 赋值给 s 的前驱
s->prior = p;
// ② 把 p->next 赋值给 s 的后继
s->next = p->next;
// ③ 把 s 赋值给 p->next 的前驱
p->next->prior = s;
// ④ 把 s 赋值给 p 的后继
p->next = s;

删除操作：

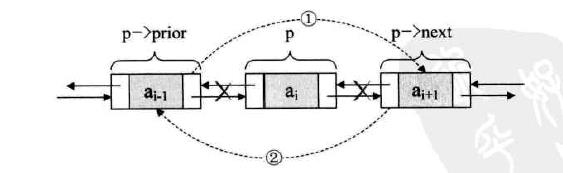
// 把 p->next 赋值给 p->prior 的后继
p->prior->next = p->next;
// 把 p->prior 赋值给 p->next 的前驱
p->next->prior = p->prior;
free(p);

3.15 总结回顾

线性表的定义：线性表是零个或多个具有相同类型的数据元素的有限序列。

线性表的顺序存储结构：用一段地址连续的存储单元依次存储线性表的数据元素，通常使用数组。

链式存储结构：不受固定的存储空间限制，可以快捷的进行插入和删除操作

以上是关于DataStruct # 线性表的主要内容，如果未能解决你的问题，请参考以下文章

[DataStructure]哈希表二叉树及多叉树 Java 代码实现

Android 底部工作表布局边距

如何通过单击片段内的线性布局从片段类开始新活动？下面是我的代码，但这不起作用

如何在android中的地图片段内中心线性布局？

单链表java简易实现

DataStruct Based on String！