数字图像处理——图像增强
Posted 牧空
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字图像处理——图像增强相关的知识,希望对你有一定的参考价值。
- 处理方法
- 空间方法
- 点处理(变换)
- 模板处理(滤波)
- 频域方法
- 空间方法
- 处理策略
- 全局处理
- 局部处理
- 处理对象
- 灰度图像
- 彩色图像
图像增强
方式
- 空间域增强:对图像的像素直接处理
- g ( x , y ) = T [ f ( x , y ) ] g(x,y) = T[f(x,y)] g(x,y)=T[f(x,y)]
- 简化后 对像素点而言 s = T ( r ) s=T(r) s=T(r)
- 频域增强:修改图像的傅里叶变换
点运算
- 反转变换
- s = ( L − 1 ) − r s=(L-1) - r s=(L−1)−r
- [ 0 , L − 1 ] [0,L-1] [0,L−1]为图像的灰度级
- 对数变换
- s = c l o g ( 1 + r ) s = clog(1+r) s=clog(1+r)
- 原图的动态范围太大,超出显示设备允许的范围,直接使用原图会丢失部分细节
- 解决方法是对原图进行灰度压缩,如对数变换
- 幂次变换
- s = c r γ s = cr^{\\gamma} s=crγ
- γ < 1 \\gamma < 1 γ<1提高灰度级,在正比函数上方,使图像变亮
- γ > 1 \\gamma > 1 γ>1降低灰度级,在正比函数下方,使图像变暗
- 对比度拉伸
- 提高图像处理时灰度级的动态范围
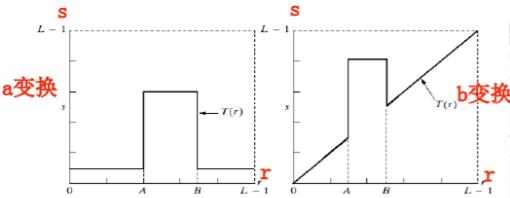
- 灰度级切片
- 关心范围指定较高值,其它指定较低值
- 关心范围指定较高值,其它保持不变
- 位平面切片
- 比如图像像素的灰度级为256,可用8位里表示,可以切分为8个1位平面,位平面0包含像素中的最低位,位平面7包含像素中的最高位
- 作用
- 通过对特定为提高亮度,改善图像质量
- 较高位包含大多数视觉重要数据
- 较低位对图像中的微笑细节由作用
- 分解为位平面可以分析每一位在图像中的相对重要性


代数运算
加法
C
(
x
,
y
)
=
A
(
x
,
y
)
+
B
(
x
,
y
)
C(x,y) = A(x,y) + B(x,y)
C(x,y)=A(x,y)+B(x,y)
主要作用
-
去除叠加性噪声
- 原图像 f ( x , y ) f(x,y) f(x,y)有一个噪声图像集 { g i ( x , y ) } , i = 1 , 2 , . . . , N , 其 中 g i ( x , y ) = f ( x , y ) + h ( x , y ) i \\{g_i(x,y)\\},i=1,2,...,N,其中g_i(x,y) = f(x,y)+h(x,y)_i {gi(x,y)},i=1,2,...,N,其中gi(x,y)=f(x,y)+h(x,y)i
- 假设 h ( x , y ) h(x,y) h(x,y)的均值为0,且互不相关,N个图像的均值定义为 g ( x , y ) = ∑ i = 0 N g i ( x , y ) N g(x,y) = \\frac{\\sum_{i=0}^{N} g_i(x,y)}{N} g(x,y)=N∑i=0Ngi(x,y)
- 期望值
E
(
g
(
x
,
y
)
)
=
f
(
x
,
y
)
E(g(x,y)) = f(x,y)
E(g(x,y))=f(x,y)
-
生成图像叠加效果
- g ( x , y ) = α f ( x , y ) + β h ( x , y ) g(x,y) = \\alpha f(x,y) + \\beta h(x,y) g(x,y)=αf(x,y)+βh(x,y)
- 图像合成或者图像衔接
减法
C
(
x
,
y
)
=
A
(
x
,
y
)
−
B
(
x
,
y
)
C(x,y) = A(x,y) - B(x,y)
C(x,y)=A(x,y)−B(x,y)
主要作用
- 显示两幅图像的差异,检测同一场景两幅图像之间的变化
- 视频中镜头边界的检测
- 去除不需要的叠加性图案
- 图像分割
乘法
C
(
x
,
y
)
=
A
(
x
,
y
)
∗
B
(
x
,
y
)
C(x,y) = A(x,y) * B(x,y)
C(x,y)=A(x,y)∗B(x,y)
主要作用
- 图像的局部显示 用二值蒙版
除法
一幅图像取反和另一幅图像相乘
逻辑运算
非
获得一个阴图像

获得一个子图像的补图像

与
作用
- 求两个子图像的相交子图
- 模板运算:提取感兴趣的子图像
或
作用
- 合并子图像
- 模板运算:提取感兴趣的子图像
异或
获得相交子图像
直方图运算
一个灰度级在范围[0,L-1]的数字图像的直方图使一个离散函数 h ( r k ) = n k h(r_k) = n_k h(rk)=nk
- n k n_k nk是图像中灰度级为 r k r_k rk的像素个数
- r k r_k rk是第k个灰度级
可定义为 p ( r k ) = n k / n p(r_k) = n_k/n p(rk)=nk/n
- 使函数值正则化到[0,1]区间
- 函数值的范围与像素的总数无关
- 给出灰度级在图像中出现的概率密度统计
直方图均衡化
使一副图像的像素占有全部可能的灰度级且分布均匀,能够具有高对比度
方法:灰度级变换 s = T ( r ) s=T(r) s=T(r)
T ( r ) T(r) T(r)需要满足以下两个条件
- T ( r ) T(r) T(r)在区间 0 ≤ r ≤ 1 0 \\leq r \\leq 1 0≤r≤1为单值且单调递增
- 0 ≤ r ≤ 1 0 \\leq r \\leq 1 0≤r≤1时, 0 ≤ T ( r ) ≤ 1 0 \\leq T(r) \\leq 1 0≤T(r)≤1
p
r
(
r
)
p_r(r)
pr(r)是
r
r
r的概率密度函数,
p
s
(
s
)
p_s(s)
ps(s)是
s
s
s的概率密度函数,
p
r
(
r
)
p_r(r)
pr(r)和
T
(
r
)
T(r)
T(r)已知,且
T
−
1
(
s
)
T^{-1}(s)
T−1(s)满足上述条件(1),所以 以上是关于数字图像处理——图像增强的主要内容,如果未能解决你的问题,请参考以下文章
p
s
(
s
)
=
p
r
(
r
)
∣
d
r
d
s
∣
(1)
p_s(s) = p_r(r)|\\frac{dr}{ds}| \\tag{1}
ps(s)=pr(r)∣dsdr∣(1)
已知只用重要的变换函数
s
=
T
(
r
)
=
∫
0
r
p
r
(
w
)
d
w
(2)
s = T(r) = \\int^r_0p_r(w)dw \\tag{2}
s=