吴恩达机器学习-2-梯度下降与正规方程
Posted 尤尔小屋的猫
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了吴恩达机器学习-2-梯度下降与正规方程相关的知识，希望对你有一定的参考价值。
公众号：尤而小屋
作者：Peter
编辑：Peter
吴恩达机器学习-2-梯度下降与正规方程
第二周主要讲解的内容包含：
- 多维特征
- 多变量梯度下降
- 梯度下降法实践
- 正规方程
多维特征Multiple Features
还是利用房价模型的例子，增加了更多的特征，比如：房间楼层、房间数量、地理位置等，构成了一个含有多个变量的模型
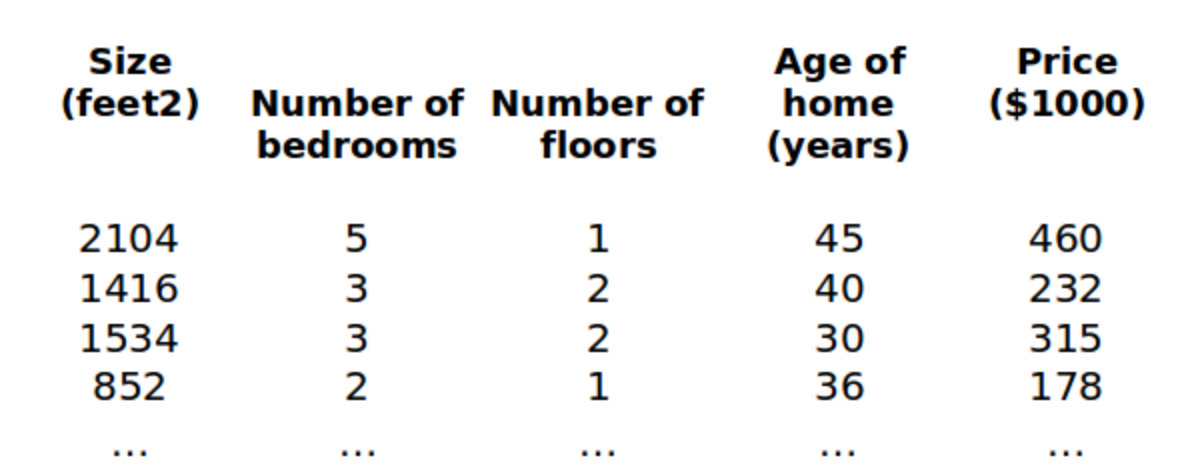
n：代表的是特征的数量
x ( i ) x^{(i)} x(i)：代表第 i i i个训练实例，是特征矩阵中的第 i i i行，是一个向量vector
x j ( i ) x^{(i)}_{j} xj(i)：表示的是第 i i i个训练实例的第 j j j个特征；i表示行，j表示列
支持多变量的假设 h h h表示为： h θ ( x ) = θ 0 + θ 1 x 1 + … + θ n x n h_{\\theta}(x)=\\theta_0+\\theta_1x_1+…+\\theta_nx_n hθ(x)=θ0+θ1x1+…+θnxn 为了简化公式，引入 x 0 = 1 x_0=1 x0=1，公式转化为： h θ ( x ) = θ 0 x 0 + θ 1 x 1 + … + θ n x n h_{\\theta}(x)=\\theta_0x_0+\\theta_1x_1+…+\\theta_nx_n hθ(x)=θ0x0+θ1x1+…+θnxn 特征矩阵X 的维度是 m ∗ ( n + 1 ) m*(n+1) m∗(n+1)，公式简化为： h θ ( x ) = θ T X h_{\\theta}{(x)}=\\theta^{T}X hθ(x)=θTX
多变量梯度下降
算法目标
与单变量线性回归类似，在多变量线性回归中，构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：
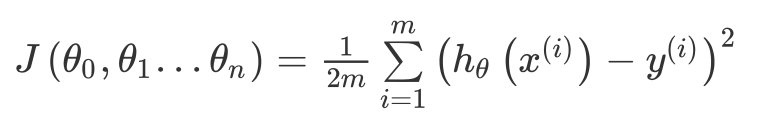
J ( θ 0 , θ 1 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\\left( {\\theta_{0}},{\\theta_{1}}...{\\theta_{n}} \\right)=\\frac{1}{2m}\\sum\\limits_{i=1}^{m}{{{\\left( h_{\\theta} \\left({x}^{\\left( i \\right)} \\right)-{y}^{\\left( i \\right)} \\right)}^{2}}} J(θ0,θ1...θn)=2m1i=1∑m(hθ(x(i))−y(i))2
其中：
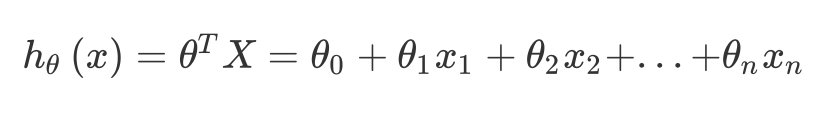
h θ ( x ) = θ T X = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\\theta}\\left( x \\right)=\\theta^{T}X={\\theta_{0}}+{\\theta_{1}}{x_{1}}+{\\theta_{2}}{x_{2}}+...+{\\theta_{n}}{x_{n}} hθ(x)=θTX=θ0+θ1x1+θ2x2+...+θnxn
算法过程
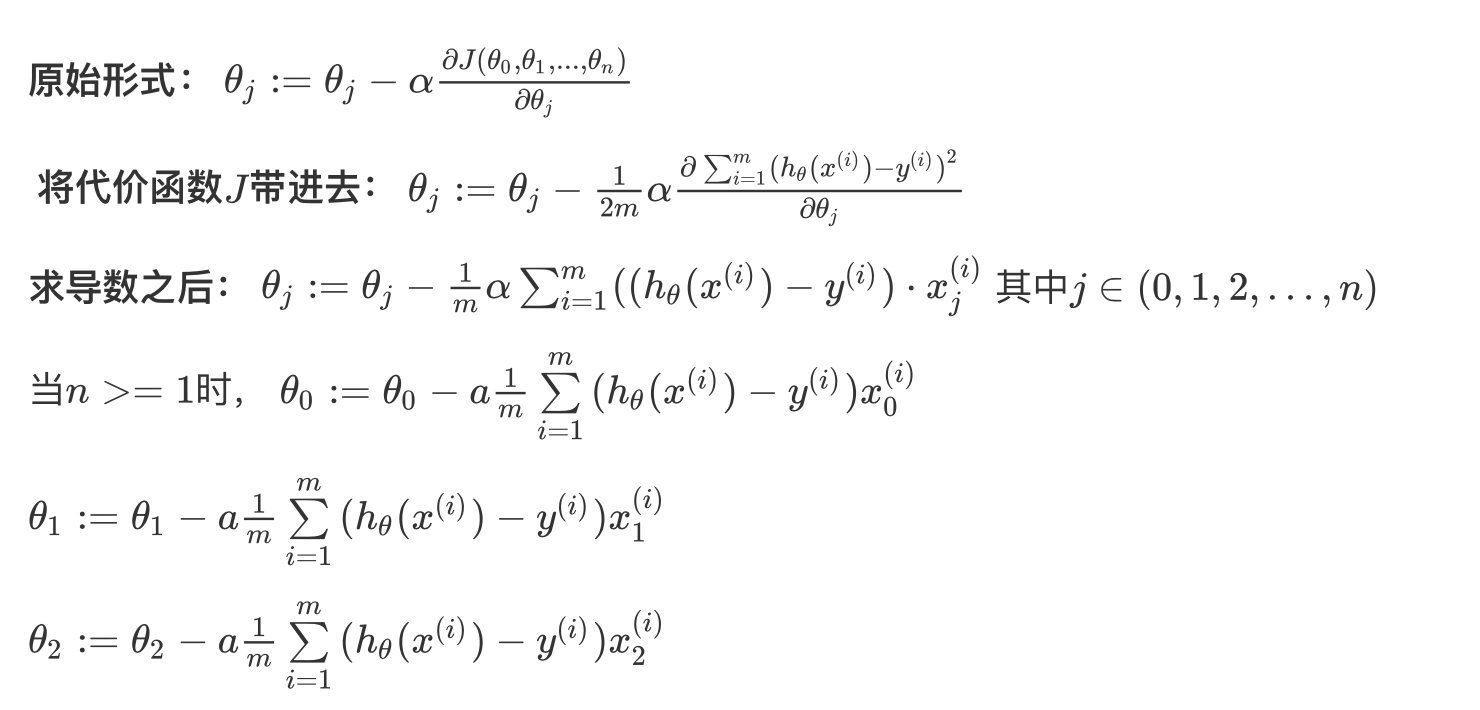
原始形式： θ j : = θ j − α ∂ J ( θ 0 , θ 1 , . . . , θ n ) ∂ θ j \\theta_j:=\\theta_j-\\alpha \\frac {\\partial J(\\theta_0,\\theta_1,...,\\theta_n)}{\\partial \\theta_j} θj:=θj−α∂θj∂J(θ0,θ1,...,θn)
将代价函数 J J J带进去： θ j : = θ j − 1 2 m α ∂ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ∂ θ j \\theta_j:=\\theta_j-\\frac{1}{2m} \\alpha \\frac {\\partial \\sum^m_{i=1}(h_{\\theta}(x^{(i)})-y^{(i)})^2}{\\partial \\theta_j} θj:=θj−2m1α∂θj∂∑i=1m(hθ(x(i))−y(i))2
求导数之后： $ \\theta_j:=\\theta_j-\\frac{1}{m} \\alpha \\summ_{i=1}((h_{\\theta}(x{(i)})-y^{(i)})\\cdot x_j^{(i)} $ 其中 j ∈ ( 0 , 1 , 2 , … , n ) j\\in{(0,1,2,…,n)} j∈(0,1,2,…,n)
当
n
>
=
1
n>=1
n>=1时，
θ
0
:
=
θ
0
−
a
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
0
(
i
以上是关于吴恩达机器学习-2-梯度下降与正规方程的主要内容，如果未能解决你的问题，请参考以下文章 斯坦福公开课-机器学习2.监督学习应用-梯度下降（吴恩达 Andrew Ng） 斯坦福公开课-机器学习2.监督学习应用-梯度下降（吴恩达 Andrew Ng） 跟着吴恩达老师学习机器学习的第七天 - logistic回归的假设函数math表达式+决策界限+代价函数+简化代价函数和logistic回归方程的梯度下降+用逻辑回归解决多类别分类问题