吴恩达机器学习-11-推荐系统
Posted 尤尔小屋的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了吴恩达机器学习-11-推荐系统相关的知识,希望对你有一定的参考价值。
公众号:尤而小屋
作者:Peter
编辑:Peter
吴恩达机器学习-11-推荐系统Recommender Systems
本周中主要讲解了推荐系统的相关知识。推荐系统应该是目前机器学习领域或者说人工智能领域最热门的方向之一,还有NLP、CV等,主要内容包含:
- 推荐系统简介
- 基于内容的推荐系统
- 协同过滤
推荐系统
推荐系统概述
常见的推荐系统有三种主要的应用常景:
- 个性化推荐:常以“推荐”、“猜你喜欢”、“发现”等形式出现,一般放在首页位置
- 相关推荐:常以“相关推荐”、“看了还看”等形式出现,一般放在内容详情页
- 热门推荐:基于各种数据进行计算,得到的排行榜,支持全局排行以及分类排行等,位置不限
推荐系统对用户的核心价值,主要表现在:
- 帮助用户便捷、快速地筛选出感兴趣的内容
- 在用户陌生的领域里面提供参考意见
- 满足用户的好奇心
推荐系统的主要工作是:
- 首先它基于用户的兴趣,根据用户的历史行为做兴趣的挖掘,把物品和用户的个性化偏好进行匹配。
- 然后通过推荐算法或者技术把信息进行过滤,解决用户的过载问题。
- 当用户有新的行为发生时,比如点击或者搜索之后,能及时进一步捕捉用户的兴趣。
- 选择合适的场景,个性化或者相关的、热门的,来给用户进行推荐。
个性化推荐系统解决的是用户很内容的关联关系,它是二者之间的桥梁。基于用户的兴趣偏好,把用户感兴趣的物品或者视频、资讯等推荐给用户,给用户带来沉浸式的体验。
问题形式化
推荐系统应用的十分广泛:如果你考虑网站像亚马逊,或网飞公司或易趣,或iTunes Genius,有很多的网站或系统试图推荐新产品给用户。如,亚马逊推荐新书给你,网飞公司试图推荐新电影给你,等等。
这些推荐系统,根据浏览你过去买过什么书,或过去评价过什么电影来判断。这些系统会带来很大一部分收入,比如为亚马逊和像网飞这样的公司。
因此对推荐系统性能的改善,将对这些企业的有实质性和直接的影响。
通过一个栗子来了解推荐系统
假使我们是一个电影供应商,我们有 5 部电影和 4 个用户,我们要求用户为电影打分

前三部是爱情片,后面两部是动作片。Alice和Bob更倾向于爱情片,Carol和Dave更倾向于动作片。一些标记
- n u n_u nu用户的数量
- n m n_m nm电影的数量
- r ( i , j ) r(i,j) r(i,j)如果用户j给电影i评过份则 r ( i , j ) = 1 r(i,j)=1 r(i,j)=1
- y ( i , j ) y^{(i,j)} y(i,j)代表的是用户j给电影i的评分
- m j m_j mj表示的是用户j评过分的电影总数
基于内容的推荐系统Content Based Recommendations
在一个基于内容的推荐系统算法中,我们假设对于我们希望推荐的东西有一些数据,这些数据是有关这些东西的特征。现在假设电影有两个特征:
- x 1 x_1 x1浪漫程度
- x 2 x_2 x2动作程度

那么每部电影都有一个特征向量,如第一部电影的是[0,9 0]
针对特征来构建一个推荐系统算法。假设使用的是线性回归模型,针对每个用户使用该模型, θ ( 1 ) \\theta^{(1)} θ(1)表示的是第一个用户的模型的参数。定义如下:
- θ ( j ) \\theta^{(j)} θ(j)第 j j j个用户的参数向量
- x ( i ) x^{(i)} x(i)电影 i i i的特征向量
针对电影 i i i和用户 j j j,该线性回归模型的代价为预测误差的平方和,加上正则化项:
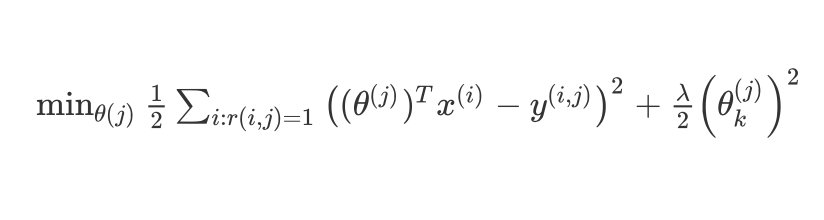
min θ ( j ) 1 2 ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ( θ k ( j ) ) 2 \\min_{\\theta (j)}\\frac{1}{2}\\sum_{i:r(i,j)=1}\\left((\\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\\right)^2+\\frac{\\lambda}{2}\\left(\\theta_{k}^{(j)}\\right)^2 θ(j)min21i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λ(θk(j))2
其中 i : r ( i , j ) i:r(i,j) i:r(i,j)表示我们只计算那些用户 j j j 评过分的电影。在一般的线性回归模型中,误差项和正则项应该都是乘以 1 / 2 m 1/2m 1/2m,在这里我们将 m m m去掉。并且我们不对方差项 θ 0 \\theta_0 θ0进行正则化处理。
针对所有用户的代价函数求和:

min θ ( 1 ) , . . . , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 \\min_{\\theta^{(1)},...,\\theta^{(n_u)}} \\frac{1}{2}\\sum_{j=1}^{n_u}\\sum_{i:r(i,j)=1}\\left((\\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\\right)^2+\\frac{\\lambda}{2}\\sum_{j=1}^{n_u}\\sum_{k=1}^{n}(\\theta_k^{(j)})^2 θ(1),...,θ(nu)min21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
如果我们要用梯度下降法来求解最优解,我们计算代价函数的偏导数后得到梯度下降的更新公式为:
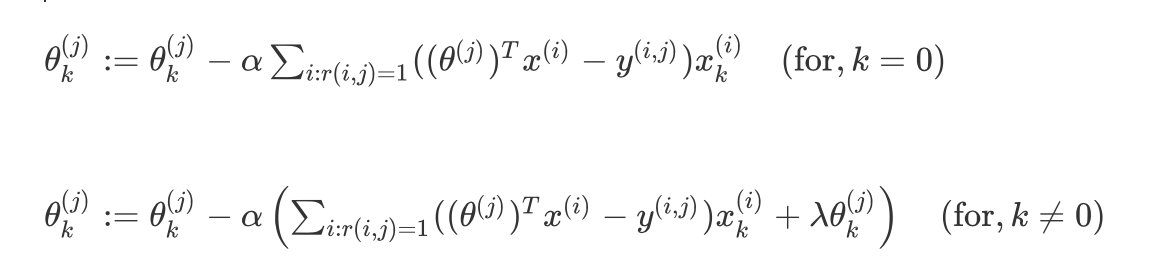
θ k ( j ) : = θ k ( j ) − α ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) ( for , k = 0 ) \\theta_k^{(j)}:=\\theta_k^{(j)}-\\alpha\\sum_{i:r(i,j)=1}((\\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)} \\quad (\\text{for} , k = 0) θk(j):=θk(j)−αi:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)(for,k=0)
θ
k
(
j
)
:
=
θ
k
(
j
)
−
α
(
∑
i
:
r
(
i
,
j
)
=
1
(
(
θ
(
j
)
)
T
x
(
i
)
−
y
(
i
,
j
)
)
x
k
(
i
)
+
λ
θ
k
(
j
以上是关于吴恩达机器学习-11-推荐系统的主要内容,如果未能解决你的问题,请参考以下文章