吴恩达机器学习-8-聚类知识
Posted 尤尔小屋的猫
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了吴恩达机器学习-8-聚类知识相关的知识,希望对你有一定的参考价值。
公众号:尤而小屋
作者:Peter
编辑:Peter
吴恩达机器学习-8-聚类
本周的主要知识点是无监督学习中的两个重点:聚类和降维。本文中首先介绍的是聚类中的K均值算法,包含:
- 算法思想
- 图解
K-Means sklearn实现Python实现
无监督学习unsupervised learning
无监督学习简介
聚类和降维是无监督学习方法,在无监督学习中数据是没有标签的。
比如下面的数据中,横纵轴都是 x x x,没有标签(输出 y y y)。在非监督学习中,我们需要将一系列无标签的训练数据,输入到一个算法中,快速这个数据的中找到其内在数据结构。
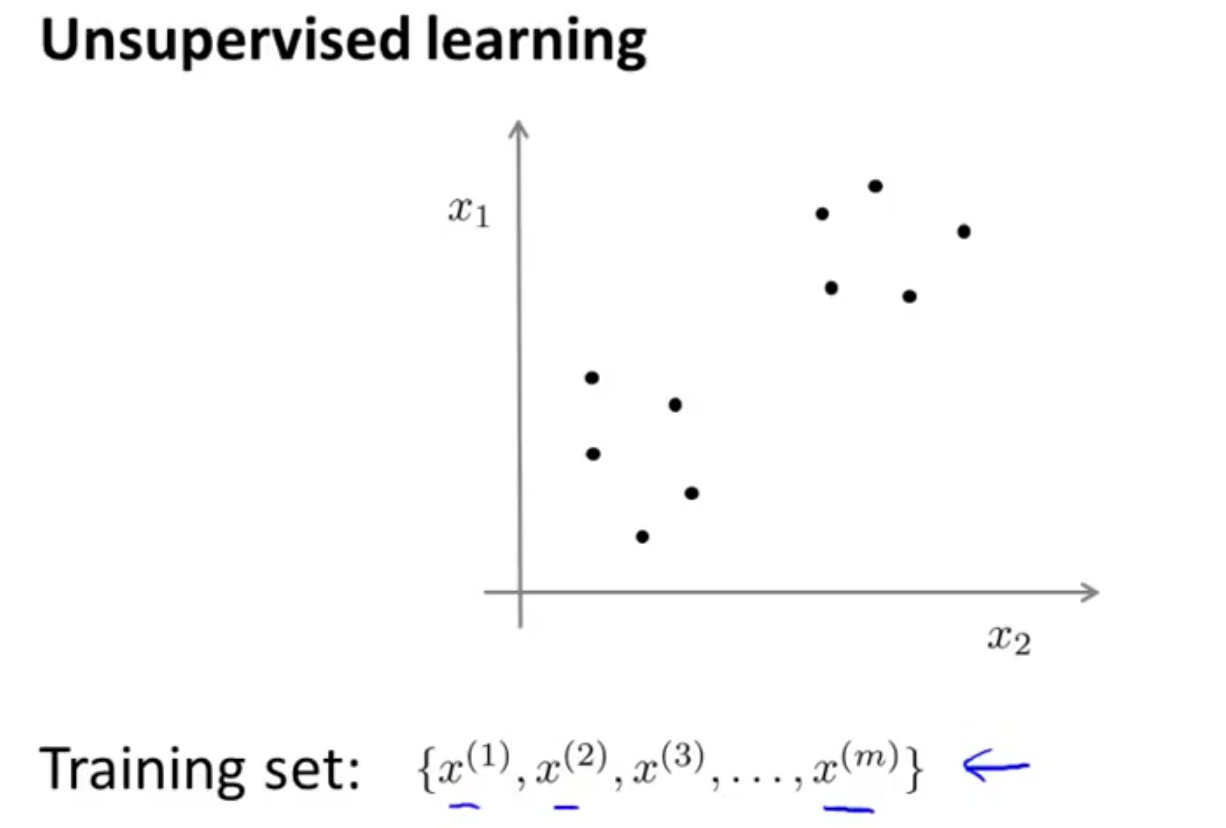
无监督学习应用
- 市场分割
- 社交网络分析
- 组织计算机集群
- 了解星系的形成

聚类
聚类clustering
聚类试图将数据集中的样本划分成若干个通常是不相交的子集,称之为“簇cluster”。聚类可以作为一个单独过程,用于寻找数据内部的分布结构,也能够作为其他学习任务的前驱过程。聚类算法涉及到的两个问题:性能度量和距离计算
性能度量
聚类性能度量也称之为“有效性指标”。希望“物以类聚”。聚类的结果是“簇内相似度高”和“簇间相似度低”。
常用的外部指标是:
- Jaccard 系数
- FM 系数
- Rand 系数
上述3个系数的值都在[0,1]之间,越小越好
常用的内部指标是:
- DB指数
- Dunn指数
DBI的值越小越好,Dunn的值越大越好。
距离计算
x i , x j x_i,x_j xi,xj的 L p L_p Lp的距离定义为:
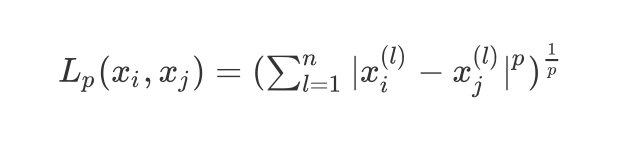
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_p(x_i,x_j)=(\\sum_{l=1}^{n}|x_i^{(l)}-x_j^{(l)}|^p)^\\frac{1}{p} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)p1
规定: p ≥ 1 p\\geq1 p≥1,常用的距离计算公式有
- 当
p
=
2
p=2
p=2时,即为
欧式距离,比较常用,即:
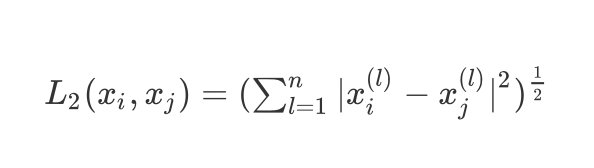
L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_2(x_i,x_j)=(\\sum_{l=1}^{n}|x_i^{(l)}-x_j^{(l)}|^2)^\\frac{1}{2} L2(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣2)21
- 当
p
=
1
p=1
p=1时,即
曼哈顿距离,即:

L 1 ( x i , x j ) = ∑ l = 1 n ( ∣ x i ( l ) − x j ( l ) ∣ ) L_1(x_i,x_j)=\\sum_{l=1}^{n}(|x_i^{(l)}-x_j^{(l)}|) L1(xi,xj)=l=1∑n(∣xi(l)−xj(l)∣)
- 当
p
p
p趋于无穷,为
切比雪夫距离,它是各个坐标距离的最大值:

L ∞ ( x i , x j ) = m a x l ∣ x i ( l ) − x j ( l ) ∣ L_{\\infty}(x_i,x_j)=\\mathop {max}\\limits_{l}|x_i^{(l)}-x_j^{(l)}| L∞(xi,xj)=lmax∣xi(l)−xj(l)∣
余弦相似度
余弦相似度的公式为:

cos ( θ ) = x T y ∣ x ∣ ⋅ ∣ y ∣ = ∑ i = 1 n x i y i ∑ i = 1 n x i 2 ∑ i = 1 n y i 2 \\cos (\\theta)=\\frac{x^{T} y}{|x| \\cdot|y|}=\\frac{\\sum_{i=1}^{n} x_{i} y_{i}}{\\sqrt{\\sum_{i=1}^{n} x_{i}^{2}} \\sqrt{\\sum_{i=1}^{n} y_{i}^{2}}} cos(θ)=∣x∣⋅∣y∣xTy=∑i=1nxi2∑i=1nyi2∑i=1nxiyi
Pearson皮尔逊相关系数
皮尔逊相关系数的公式如下:
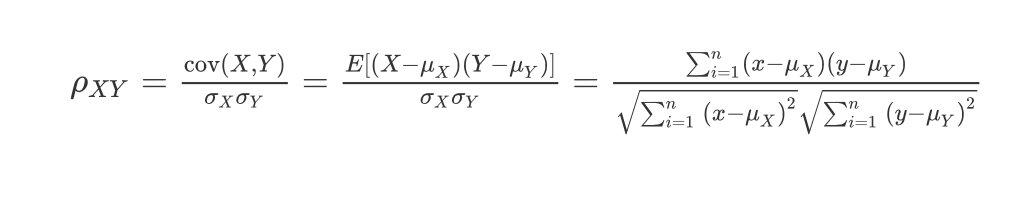
ρ X Y = cov ( X , Y ) σ X σ Y = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y = ∑ i = 1 n ( x − μ X ) ( y − μ Y ) ∑ i = 1 n ( x − μ X ) 2 ∑ i = 1 n ( y − μ Y ) 2 \\rho_{X Y}=\\frac{\\operatorname{cov}(X, Y)}{\\sigma_{X} \\sigma_{Y}}=\\frac{E\\left[\\left(X-\\mu_{X}\\right)\\left(Y-\\mu_{Y}\\right)\\right]}{\\sigma_{X} \\sigma_{Y}}=\\frac{\\sum_{i=1}^{n}\\left(x-\\mu_{X}\\right)\\left(y-\\mu_{Y}\\right)}{\\sqrt{\\sum_{i=1}^{n}\\left(x-\\mu_{X}\\right)^{2}} \\sqrt{\\sum_{i=1}^{n}\\left(y-\\mu_{Y}\\right)^{2}}} ρXY=σXσYcov(X,Y)=以上是关于吴恩达机器学习-8-聚类知识的主要内容,如果未能解决你的问题,请参考以下文章