向量点乘和叉乘

Posted 2021-06-05 StriveZs

---

title: 向量点乘和叉乘

categories:

• Math

tags:

• Math
• Knowledge

---

向量点乘和叉乘

假设存在向量a和向量b:$ a=[a_{1},a_{2},a_{3}],b=[b_{1},b_{2},b_{3}] $

点乘

向量a和向量b的点乘公式如下:

$ a\\bullet b=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} $

要求是向量a和向量的b的维度要相同。

点乘的几何意义

点乘的几何意义是可以用来表征或者计算两个向量之间的夹角，以及在b向量或在a向量方向上的投影，公式如下:

$ a\\bullet b=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=|a||b|cos \\theta $

首先假设一下向量构成:

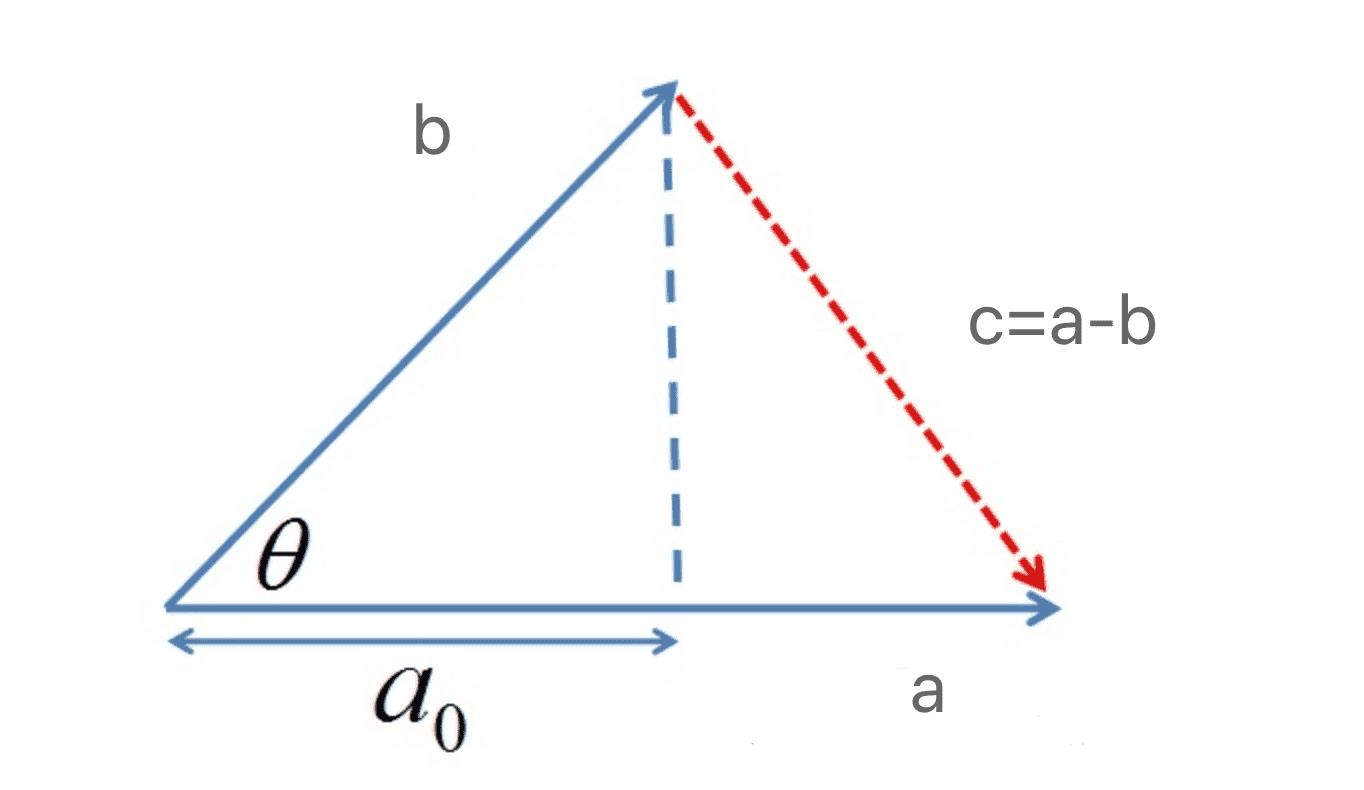
推导过程如下:

• 根据上图可以得到c=a-b
• 根据三角余弦定理可以得到: $ c^{2}=a^{2}+b^{2}-2|a||b|cos \\theta$
• 根据c=a-b，我们可以对上式变换得到 $ (a-b) \\bullet(a-b)=a^{2}+b^{2}-2 a \\bullet b=a^{2}+b^{2}-2|a \\| b| \\cos \\theta $
• 化简上式我们可以得到: $ a\\bullet b=|a||b|cos \\theta $
• 因此在已知向量a和向量b长度的情况下，我们可以计算得到a和b的夹角θ
• $ \\theta=arc\\: cos\\left ( \\frac{a \\bullet b}{|a||b|} \\right ) $

根据上述公式就可以计算向量a和向量b之间的夹角，从而就进一步判断出这两个向量是否是同一方向，是否正交，具体对应关系如下:

• a·b>0 : 方向基本相同，夹角在0到90度之间
• a·b=0 : 两个向量正交，相互垂直
• a·b<0 : 方向基本相反，夹角在90度到180度之间

叉乘

两个向量的叉乘，又叫向量积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉乘与这两个向量组成的坐标平面垂直
同样是使用之前假设的向量a和向量b，我们可以得到向量a和向量b的叉乘公式:

$ a \\times b=\\left|\\begin{array}{lll}\\mathrm{i} & \\mathrm{j} & \\mathrm{k} \\\\a_{1} & a_{2} & a_{3} \\\\b_{1} & b_{2} & b_{3}\\end{array}\\right|=\\left(a_{2}b_{3}-a_{3}b_{2}\\right) i-\\left(a_{1}b_{3}-a_{3}b_{1}\\right) j+\\left(a_{1}b_{2}-a_{2}b_{1}\\right) k $

其中$ i=(1,0,0),j=(0,1,0),k=(0,0,1) $, 其中ijk均为单位向量，最后叉乘的结果为一个向量，所以ijk要为向量，因此单纯的ab相乘再相减得到的标量。
因此根据上述i、j、k间的关系，有如下式子(直接用向量表示):

$ a\\times b=\\left( a_{2}b_{3}-a_{3}b_{2}, a_{1}b_{3}-a_{3}b_{1}, a_{1}b_{2}-a_{2}b_{1} \\right) $

注意: 一个向量叉乘自己得到的是0向量，根据右手定则，叉乘得到的结果无论怎么旋转都会永远会垂直这个向量，因此只有0向量满足。

叉乘的几何意义

在三维几何中，向量a和向量b的叉乘结果是一个向量，这个向量又称为法向量，它是a和b构成的平面的法向量(垂直)。

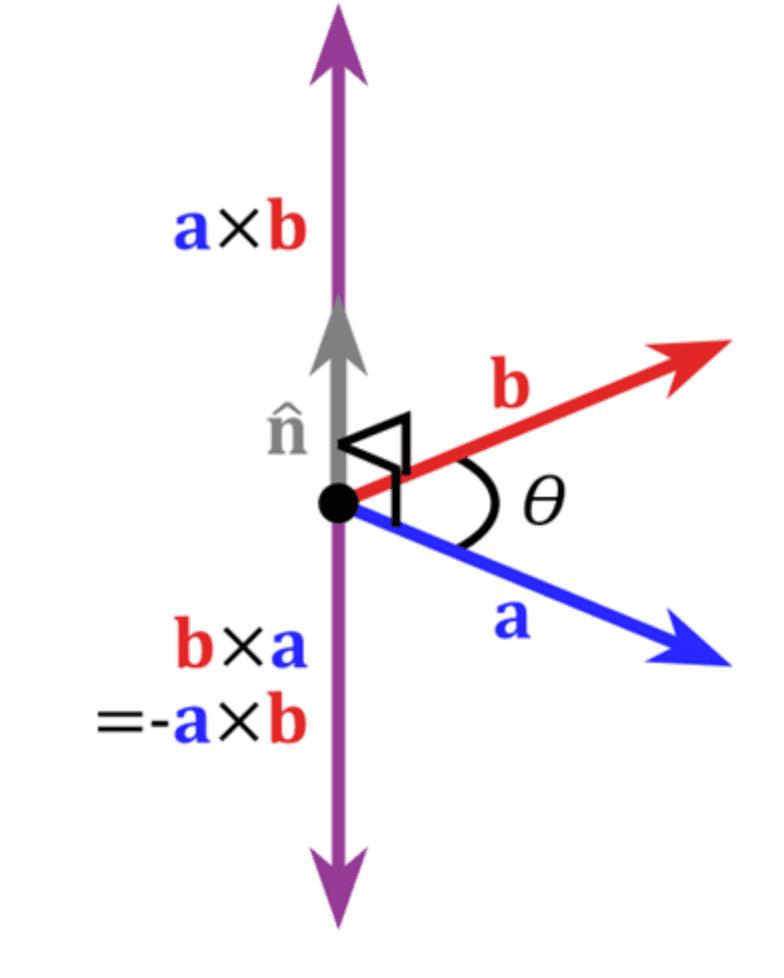
如上图。

右手法则：使用右手法则来判断a×b向量的方向,如下图所示

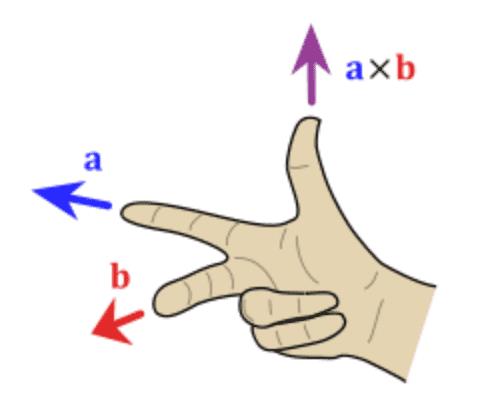
判断方法如下:

• 右手手掌张开，四指并拢，大拇指垂直于四指指向的方向
• 伸出右手，四指弯曲，四指与A旋转到B方向一致，那么大拇指指向为C向量的方向