Java高频面试之：二叉树

Posted 2021-03-30 编程那些烦心事

不点蓝字，我们哪来故事？

面试官：什么是二叉树？了解吗？

我：哦，知道。二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分。二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点。

面试官：那二叉树的前序、中序、后序遍历了解吗？

我：我还点事，先走了。

什么是二叉树的前、中、后序遍历？

为什么要叫前序、中序、后序遍历这种名字？因为是根据根节点的顺序来命名的。

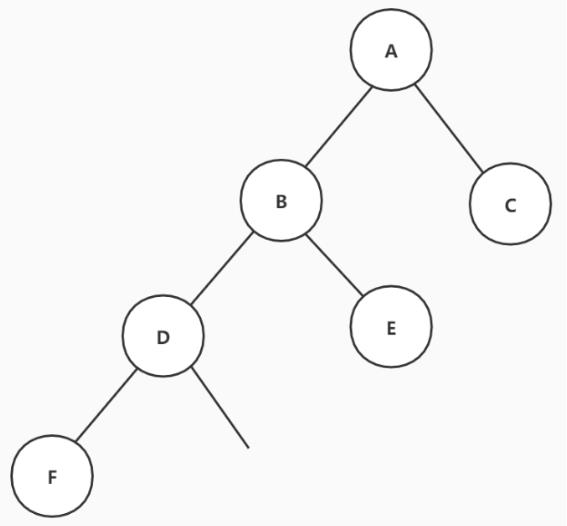
1.先来一个简单的例子，如下是一个满节点

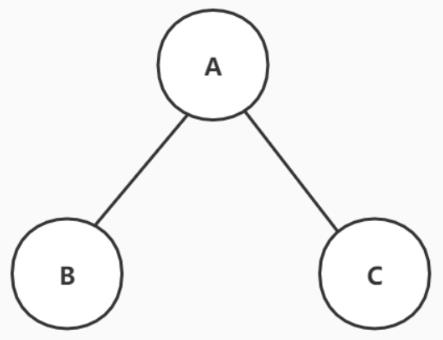
遍历的顺序

• 前序遍历：ABC（先根节点，然后同级先左后右）

• 中序遍历：BAC（先左后根最后右）

• 后序遍历：BCA（先左子树，后右子树，再根节点）

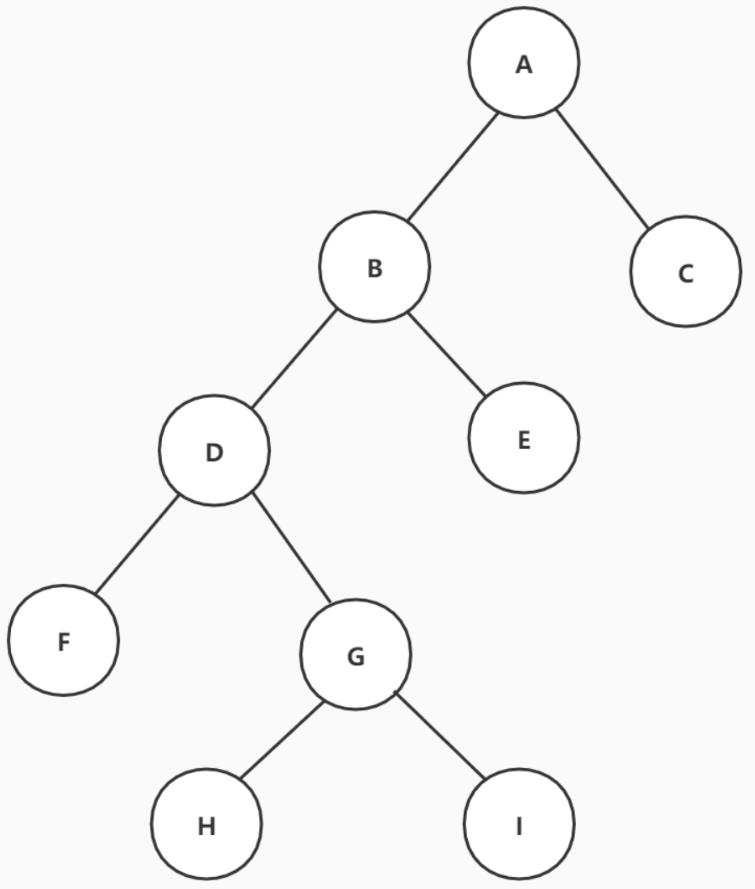
2.再看一个稍微复杂点的二叉树

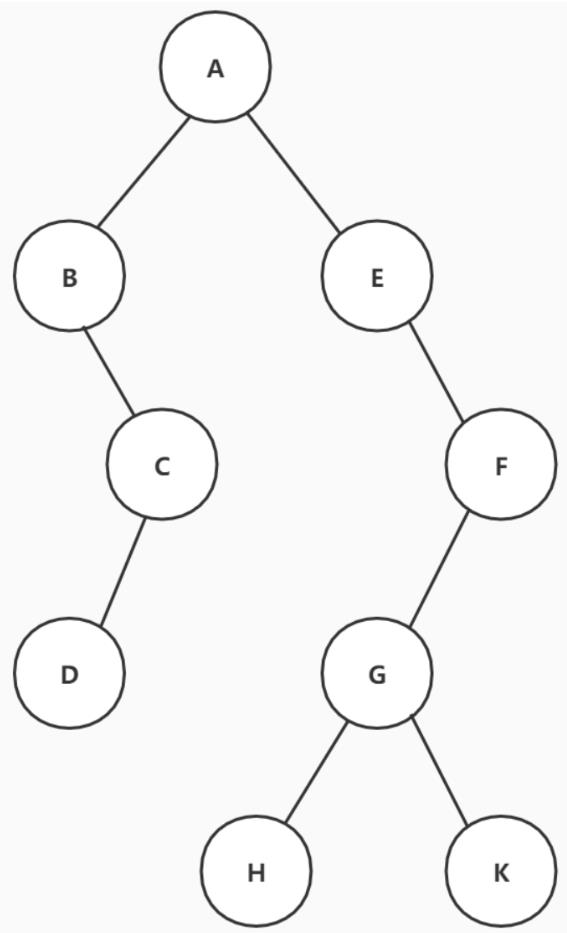
这个树的遍历顺序是怎么样的？

• 前序遍历：ABCDEFGHK

• 中序遍历：BDCAEHGKF

• 后序遍历：DCBHKGFEA

前序遍历比较简单，我们就不分析了，我们看一下中序遍历的过程：

• A左边有节点，我们先遍历A左边的节点（_ _ _ A _ _ _ _ _）

• B左边没有节点，先B，然后遍历B右边的节点（B _ _ A  _ _ _ _ _）

• C左边有节点D，D是末节点（B D C A  _ _ _ _ _）

• 根节点A所有的左节点遍历完成，开始遍历右节点，E没有左节点，所以先E（B D C A E _ _ _ _）

• F有左节点G，G有左节点H，H是末节点（B D C A E H G _ _）

• G有右节点K（B D C A E H G K _）

• F没有右节点（B D C A E H G K F）

再看一下后序遍历的过程：

• A有左节点和右节点（_ _ _ _ _ _ _ _ A）

• B有右节点C，C有左节点D，D是末节点（D C B _ _ _ _ _ A）

• 然后开始遍历右节点E，节点E没有左节点，所以先看右节点F，节点F有左节点G，节点G有左节点H和右节点K，均是末节点（D C B H K G _ _ A）

• F没有右节点（D C B H K G F E A）

好了，现在二叉树的前、中、后序遍历的概念搞清楚了。我们再来进阶一下。

例题1

已知某二叉树的前序遍历为A B D F G H I E C，中序遍历为F D H G I B E A C，请还原这颗二叉树。

解题思路：

• 从前序遍历中，我们确定了根节点为A。

• 从中序遍历中，确定了F D H G I B E在根节点A的左边，C在根节点A的右边。

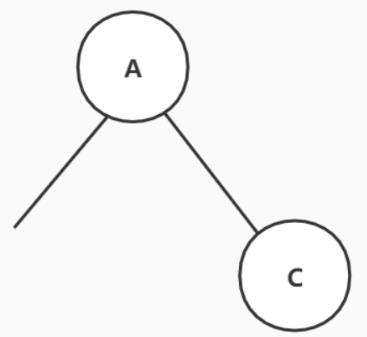
• 那么剩下的前序遍历为B D F G H I E，中序遍历为F D H G I B E， B就是我们新的“根结点”，从中序遍历可以确定F D H G I在B的左边，E在B的右边。

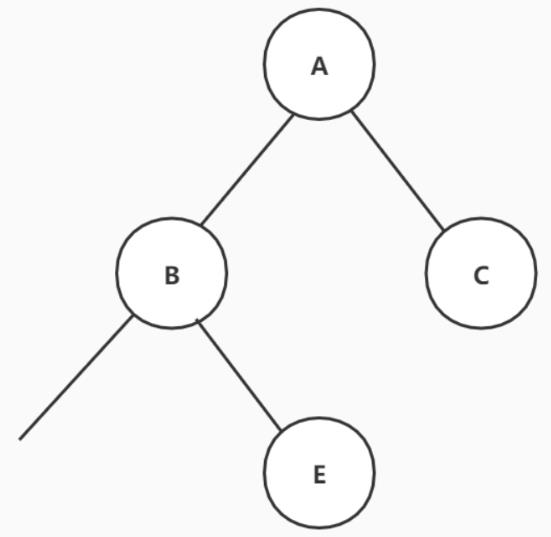
• 那么现在前序遍历剩下D F G H I，中序遍历剩下F D H G I。那么D就是我们新的“根节点”。根据中序遍历可以确定F在D的左边，H G I在D的右边。

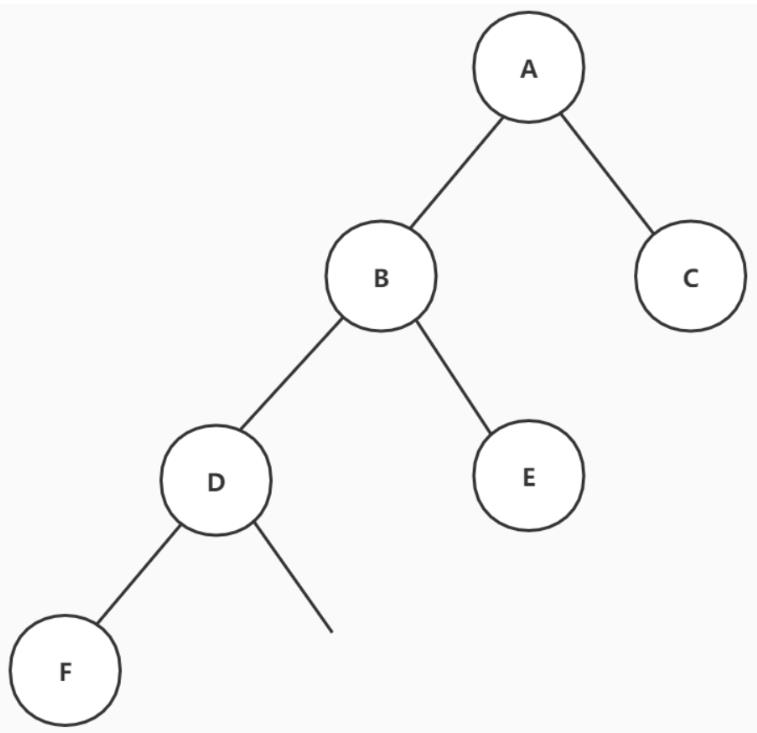
• 现在前序遍历剩下G H I，中序遍历剩下H G I，根据前序遍历可以确定G为新的“根节点”，根据中序遍历可以确定H在G的左边，I在G的右边。

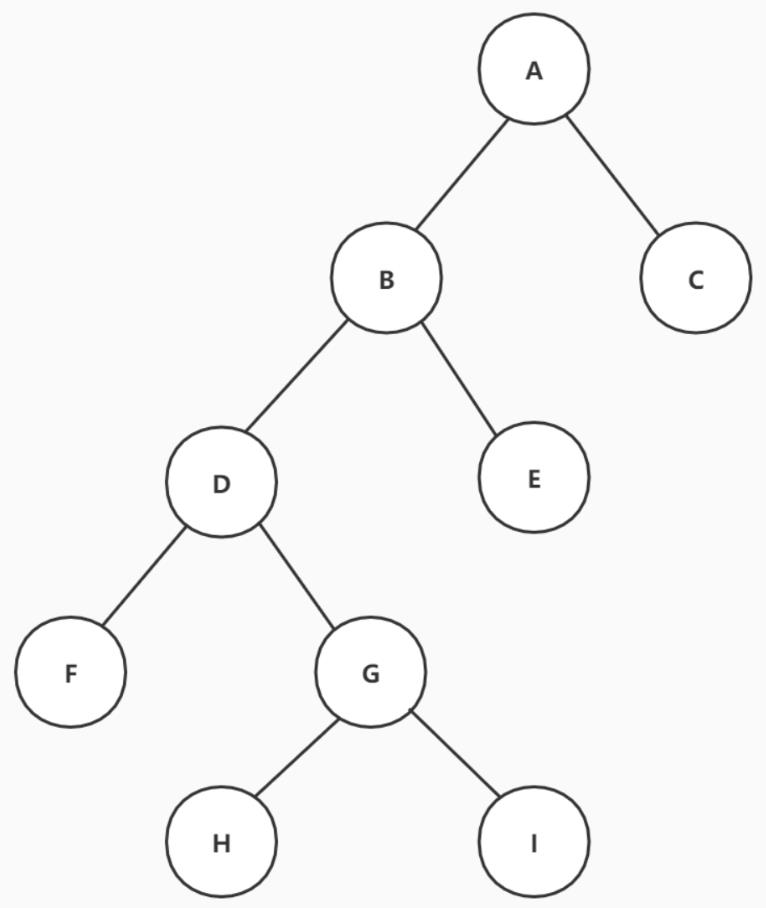
好了，这样的我们的二叉树就构建完成啦。

例题2

已知某二叉树的中序遍历为F D H G I B E A C，后序遍历为F H I G D E B C A，请还原这颗二叉树。

解题思路：

• 从后序遍历可以确定根节点是A，根据中序遍历可以确定F D H G I B E在A的左边，C在A的右边。

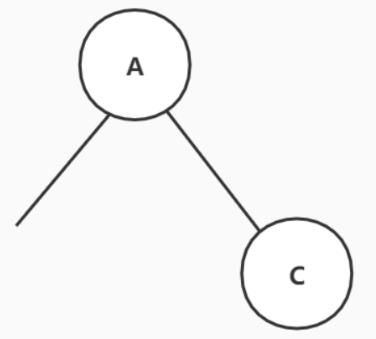
• 现在中序遍历剩下F D H G I B E，后序遍历剩下F H I G D E B，根据后序遍历我们可以确定B为新的“根节点”，根据中序遍历我们可以确定F D H G I在B的左边，E在B的右边。

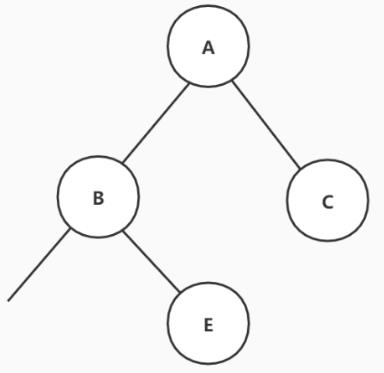
• 现在中序遍历剩下F D H G I，后序遍历剩下F H I G D，根据后序遍历可以确定D为新的“根节点”，根据中序遍历可以确定F在D的左边，H G I在D的右边。

• 现在中序遍历剩下H G I，后续遍历剩下H I G，根据后序遍历可以确定G为新的“根节点”，根据中序遍历可以确定H在G的左边，I在G的右边。

例题3

光有前序和后序遍历，无法还原二叉树。

代码实现前中后序遍历

那么如果我们是用代码，怎么来实现我们的前中后序遍历呢？

我们先构建一棵树

public class Node { private int data; private Node leftNode; private Node rightNode;
 public Node(int data, Node leftNode, Node rightNode){ this.data = data; this.leftNode = leftNode; this.rightNode = rightNode; } public int getData() { return data; } public void setData(int data) { this.data = data; } public Node getLeftNode() { return leftNode; } public void setLeftNode(Node leftNode) { this.leftNode = leftNode; } public Node getRightNode() { return rightNode; } public void setRightNode(Node rightNode) { this.rightNode = rightNode; }}

递归版本前序、中序、后序遍历

public class BinaryTreeRecurDemo { /** * 注意必须逆序建立，先建立子节点，再逆序往上建立， * 因为非叶子结点会使用到下面的节点，而初始化是按顺序初始化的，不逆序建立会报错。 */ public Node init() { Node J = new Node(8, null, null); Node H = new Node(4, null, null); Node G = new Node(2, null, null); Node F = new Node(7, null, J); Node E = new Node(5, H, null); Node D = new Node(1, null, G); Node C = new Node(9, F, null); Node B = new Node(3, D, E); Node A = new Node(6, B, C); // 返回根节点 return A; }
 public void printNode(Node node) { System.out.println(node.getData()); }
 /** * 前序遍历 */ public void preOrder(Node root) { printNode(root); if (root.getLeftNode() != null) { // 递归遍历左孩子 preOrder(root.getLeftNode()); } if (root.getRightNode() != null) { // 递归遍历右孩子 preOrder(root.getRightNode()); } }
 /** * 中序遍历 */ public void infixOrder(Node root) { if (root.getLeftNode() != null) { infixOrder(root.getLeftNode()); } printNode(root); if (root.getRightNode() != null) { infixOrder(root.getRightNode()); } }
 public void afterOrder(Node root) { if (root.getLeftNode() != null) { afterOrder(root.getLeftNode()); }
 if (root.getRightNode() != null) { afterOrder(root.getRightNode()); } printNode(root); }
 public static void main(String[] args) { BinaryTreeRecurDemo tree = new BinaryTreeRecurDemo(); Node root = tree.init(); System.out.println("=======> 前序遍历"); tree.preOrder(root); System.out.println("=======> 中序遍历"); tree.infixOrder(root); System.out.println("=======> 后序遍历"); tree.afterOrder(root); }}

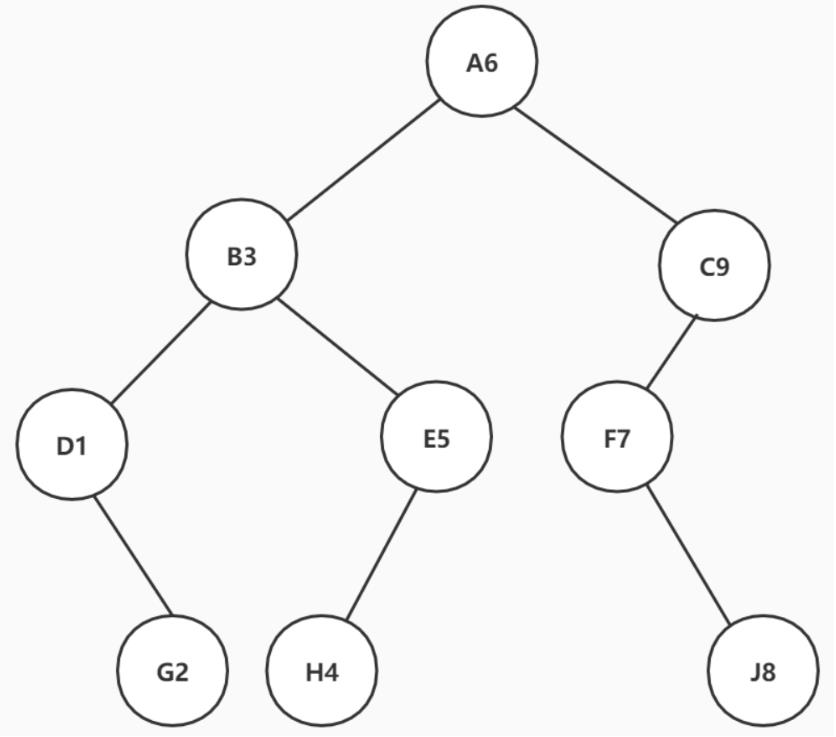
init()方法构建出来的是这样一棵树

执行main()方法

=======> 前序遍历631254978=======> 中序遍历123456789=======> 后序遍历214538796

验证结果正确！

非递归版本前序、中序、后序遍历

如果不用递归的方式，可以不可以实现前序、中序、后序遍历呢？

当然可以，我们可以用堆栈

public class BinaryTreeStackDemo { public Node init() { Node J = new Node(8, null, null); Node H = new Node(4, null, null); Node G = new Node(2, null, null); Node F = new Node(7, null, J); Node E = new Node(5, H, null); Node D = new Node(1, null, G); Node C = new Node(9, F, null); Node B = new Node(3, D, E); Node A = new Node(6, B, C); // 返回根节点 return A; }
 public void printNode(Node node) { System.out.println(node.getData()); }
 /** * 前序遍历 */ public void preOrder(Node root) { Stack<Node> stack = new Stack<Node>(); Node node = root; while (node != null || stack.size() > 0) { // 将所有左孩子压入栈 if (node != null) { // 压入栈之前先访问 printNode(node); stack.push(node); node = node.getLeftNode(); } else { node = stack.pop(); node = node.getRightNode(); } } }
 /** * 中序遍历 */ public void infixOrder(Node root) { Stack<Node> stack = new Stack<Node>(); Node node = root; while (node != null || stack.size() > 0) { if (node != null) { // 直接压入栈 stack.push(node); node = node.getLeftNode(); } else { // 出栈并访问 node = stack.pop(); printNode(node); node = node.getRightNode(); } } }
 /** * 后序遍历 */ public void afterOrder(Node node){ if (node==null) { return; } Stack<Node> s = new Stack<Node>(); // 当前访问的结点 Node curNode; // 上次访问的结点 Node lastVisitNode; curNode = node; lastVisitNode = null;
 // 把currentNode移到左子树的最下边 while (curNode!=null) { s.push(curNode); curNode = curNode.getLeftNode(); } while (!s.empty()) { // 弹出栈顶元素 curNode = s.pop(); // 一个根节点被访问的前提是：无右子树或右子树已被访问过 if (curNode.getRightNode()!=null&&curNode.getRightNode()!=lastVisitNode) { // 根节点再次入栈 s.push(curNode); // 进入右子树，且可肯定右子树一定不为空 curNode = curNode.getRightNode(); while (curNode!=null) { // 再走到右子树的最左边 s.push(curNode); curNode = curNode.getLeftNode(); } } else { // 访问 System.out.println(curNode.getData()); // 修改最近被访问的节点 lastVisitNode = curNode; } } }
 public static void main(String[] args) { BinaryTreeStackDemo tree = new BinaryTreeStackDemo(); Node root = tree.init(); System.out.println("=======> 前序遍历"); tree.preOrder(root); System.out.println("=======> 中序遍历"); tree.infixOrder(root); System.out.println("=======> 后序遍历"); tree.afterOrder(root); }}

后序遍历稍微复杂些，可以看注释，输出结果

=======> 前序遍历631254978=======> 中序遍历123456789=======> 后序遍历214538796

结果和递归版本是一样的。

Hi

感谢你的到来

我不想错过你

编程那些烦心事

精彩推荐

喜欢就点个在看再走吧