路径规划基于萤火虫算法求解含障碍的路径规划问题matlab源码

Posted 2021-06-05 博主QQ2449341593

仿生群智能优化算法是近些年来国内外学者研究的热点问题，其主要的思想是研究或者模仿自然界群体生活的生物的社会行为而构造的随机搜索方法。目前研究比较多的有两种算法：蚁群算法（ACO）和粒子群算法（PSO）。有研究结果表明，仿生群智能优化算法为许多应用领域提供了新思路和新方法。
  2005年，印度学者K.N.Krishnanand和D.Ghose在IEEE群体智能会议上提出了一种新的群智能优化算法，人工萤火虫群优化（Glowworm Swarm Optimization, GSO）算法。2009年，剑桥学者Xin-She Yang根据自然界中萤火虫的发光行为提出萤火虫算法（Firefly Algorithm, FA）。自这两种萤火虫算法提出以来，各国学者对这两种算法进行了研究、改进和应用。经过几年的发展，在连续空间的寻优过程和一些生产调度方面萤火虫算法具有良好的应用前景。
  GSO和FA有相似的方面，但在具体实现方面有一定差异。本文具体介绍和分析了这两种算法及其改进算法。

GSO算法

  在GSO算法中，每一只人工萤火虫散步在解空间中，这些萤火虫带着荧光，并且拥有各自的视线范围，称为决策域（local-decision range）。它们的亮度与自己所在位置上的目标值有关。越亮的萤火虫表示它所在的位置越好，即有较优的目标函数值。萤火虫会在决策域范围内寻找邻居集合，在集合当中，越亮的邻居拥有越高的吸引力吸引此萤火虫往这个方向移动，每一次的飞行方向会随着挑选的邻居不同而改变。此外，决策域范围的大小会受到邻居数量的影响，当邻居密度越低，萤火虫的决策半径会加大以寻找更多的邻居；当邻居密度越高，它的决策半径会缩小。最后，大部分萤火虫会聚集在多个位置上，即达到极值点。简单的说，GSO算法主要包含四个阶段：萤火虫的部署（初始化）、荧光素更新、位置更新阶段和决策半径更新阶段。

7.1.1 闪光模式

随着进化，萤火虫已经进化到可以通过多种方式控制光的发射，从而产生不同的交配信号。它们通过改变如下参数来产生不同的信号：

• 发光的颜色；
• 发光的亮度；
• 雄性闪光和雌性闪光-相位差；
• 每次闪光持续时间；
• 每周期闪光次数；
• 闪光时间；
• 连续发光或闪光脉冲序列。

Kaipa和Ghose (2017)用不同的例子来描述这些闪光模式，例如使用Lampyrus萤火虫，一种在欧洲常见的萤火虫，只有雌性才有发光的能力。她在草地上扭动着身体，把光线从一个方向扫到另一个方向，以吸引四处游荡的雄性萤火虫的注意。对于Lamprophorustenebrosus萤火虫，雄性和雌性都具有发光能力，但雌性没有翅膀，其类似于Lampyrus，利用光线吸引配偶。在一些物种中，雌性使用不同的模式，如长闪光发光，在间隔时间内并不完全熄灭。当雄性在10英尺远的地方能感觉到这种模式时，它们就会飞向雌性。这些闪光模式是物种特有的，例如在Photinus这一类萤火虫中，雄性通过在地面上爬行开始交配，发出各种各样的光，并观察附近雌性的反应信号。在Photinus consanguineus中，雄萤火虫发出两道闪光，雄萤火虫停顿一下，接着又发出两道闪光，它重复这个模式。在雄性发出第二次闪光后，雌性会在一秒钟内做出回应。在Photinus castus中，雄萤火虫发出长长的闪光，雌萤火虫立即做出回应。尽管P. consanguineus和P. castus的结构非常类似，但根据它们发光的模式不同，它们被认为是不同的物种。尽管它们经常一起飞行，但是不会出现杂交的情况，但根据它们发光的模式不同，它们被认为是不同的物种，但它们经常一起飞行。

 群体交配

上面提到的物种有一个共同点，不管是雄性还是雌性，不管是谁在吸引另一个，都需要一个不间断的视线，这样他们才能感知到信号并做出回应。在一些视觉杂乱的地区，比如东南亚的红树林沼泽，要获得如此不间断的视线并不容易。因此，在这些地区发现的物种没有选择个体求偶。这里的萤火虫而是在树上或洞穴里成群结队，因为这样游走的萤火虫就很容易找到交配对象。如果最初没有群体，那么通过相互的光吸引，萤火虫可能会形成一个核团。在形成这些群体的过程中存在着竞争，这就导致了不止一个更大的群体，而这些更大的群体会进一步吸引附近更小的核，因为它们的平均光发射量更高，这意味着找到配偶的可能性更高。

 萤火虫群优化算法

针对萤火虫和萤火虫群的行为，Krishnanand和Ghose（2005）[1]提出了萤火虫群优化算法（Glowworm Swarm Optimization，GSO），并使用于诸多应用。最初，GSO的开发目标是提供数值优化问题的解决方案，而不是确定全局最优，但是由于GSO的分散决策和移动协议，它在机器人等领域做出了更多的贡献。

最初受萤火虫启发，GSO在随机搜索空间中随机分布一组或一群代理，代理间通过其他行为机制相互影响，而这些机制在其自然界中的对应物中是不存在的。算法的基本工作基于以下三种机制：

1. 适应度广播
   萤火虫有一种叫做荧光素（luciferin）的色素，可以使萤火虫发光。萤火虫体内荧光素的含量决定了它们在目标空间中的位置的适应度。
2. 正趋性
   萤火虫被比自己亮的邻居吸引，因此开始向它移动。当有多个这样的邻居时，它利用概率机制来选择一个。
3. 自适应邻域
   每个萤火虫利用一个自适应邻域来识别邻居，该邻域由一个具有可变范围rdi的局部决策域定义，该域的边界是一个硬限制的感知范围rs(0<rdi<rs)。这里可以使用一种合适的启发式方法来调节rdi。萤火虫的运动完全依赖于局部信息，每个萤火虫都会选择一个邻居，这个邻居的荧光素值大于它自己的荧光素值，然后向它靠近。这些运动建立在可用的局部信息和选择性的邻居交互的基础上，使得萤火虫群能够聚集成不相交的子群，朝着给定多峰函数的多个最优值移动并在其上相遇。

 算法

虽然该算法被解释为寻找多峰函数的多个最优解，但可以通过简单修改用于最小化问题。最初，GSO将萤火虫随机地放置在搜索空间中，使它们分布得很好。初始时，每只萤火虫体内的荧光素含量为零。该算法的单位周期包括荧光素更新阶段、移动阶段和邻域范围更新阶段，如图1所示。

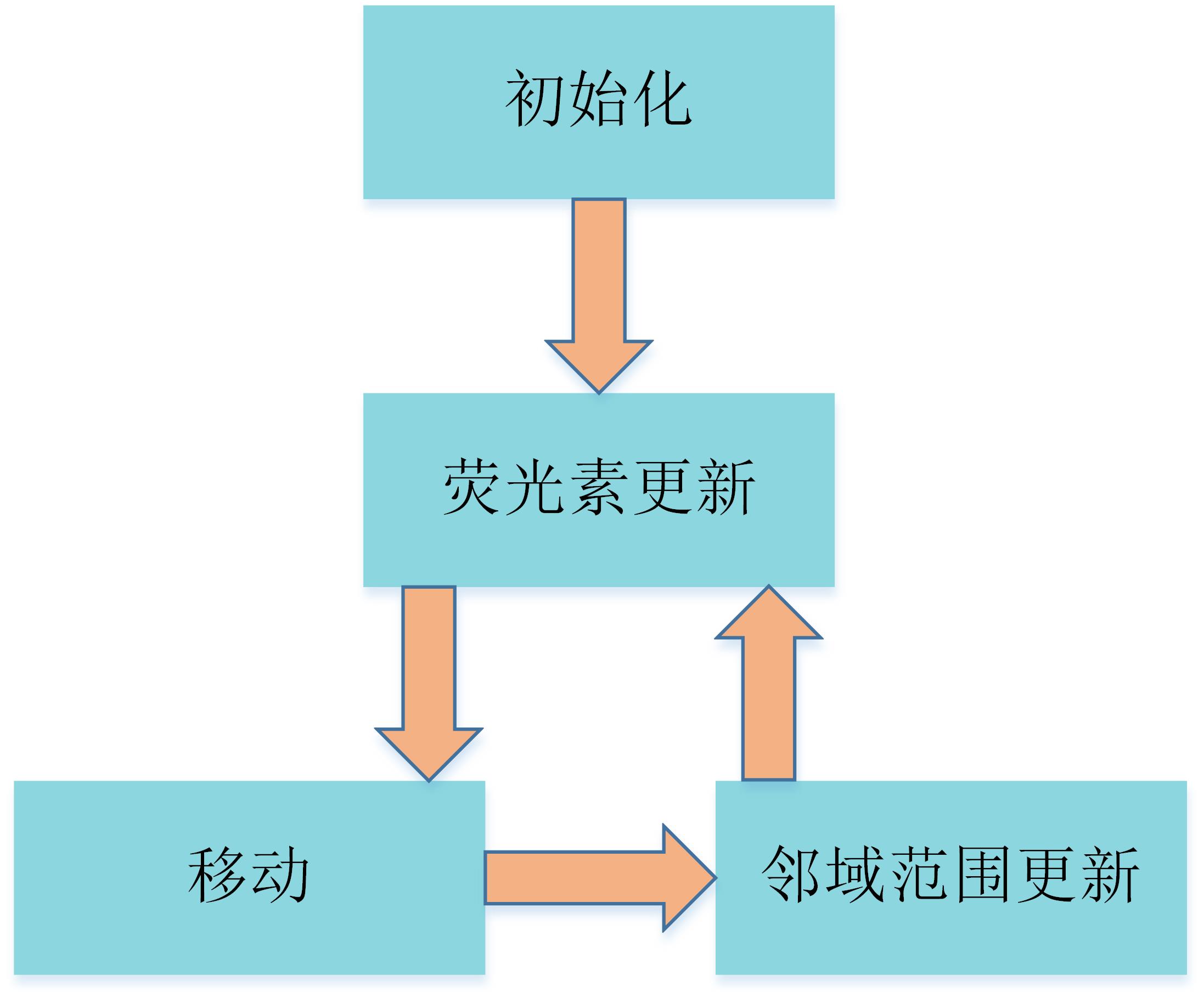
图1 GSO算法流程

clc;
clear;
close all;
 
%% Problem Definition
 
model=CreateModel();
 
model.n=3;  % number of Handle Points
 
CostFunction=@(x) MyCost(x,model);    % Cost Function
 
nVar=model.n;       % Number of Decision Variables
 
VarSize=[1 nVar];   % Size of Decision Variables Matrix
 
VarMin.x=model.xmin;           % Lower Bound of Variables
VarMax.x=model.xmax;           % Upper Bound of Variables
VarMin.y=model.ymin;           % Lower Bound of Variables
VarMax.y=model.ymax;           % Upper Bound of Variables
 
 
%% GSO Parameters
 
MaxIt=50;          % Maximum Number of Iterations
 
nPop=100;           % Population Size (Swarm Size)
 
w=1;                % Inertia Weight
wdamp=0.98;         % Inertia Weight Damping Ratio
c1=1.5;             % Personal Learning Coefficient
c2=1.5;             % Global Learning Coefficient
 
%RANGE
range_init = 5.0;
range_boundary = 50.2;
 
%LUCIFERIN
luciferin_init = 25;
luciferin_decay = 0.4;
luciferin_enhancement = 0.6;
 
%Neighbors
k_neigh = 20;
beta = 0.5;
 
step_size = 5;
 
%% Initialization
 
% Create Empty Glowworm Structure
empty_glowworm.Position=[];
empty_glowworm.range=[];
empty_glowworm.luciferin=[];
empty_glowworm.Cost=[];
empty_glowworm.Sol=[];
empty_glowworm.neighbors=[];
empty_glowworm.Best.Position=[];
empty_glowworm.Best.Cost=[];
empty_glowworm.Best.Sol=[];
 
% Initialize Global Best
GlobalBest.Cost=inf;
 
% Create glowworms Matrix
glowworm=repmat(empty_glowworm,nPop,1);
 
% Initialization Loop
for i=1:nPop
	% Initialize Position
    if i > 1
        glowworm(i).Position=CreateRandomSolution(model);
    else
        % Straight line from source to destination
        xx = linspace(model.xs, model.xt, model.n+2);
        yy = linspace(model.ys, model.yt, model.n+2);
        glowworm(i).Position.x = xx(2:end-1);
        glowworm(i).Position.y = yy(2:end-1);
    end
 
    % Initialize luciferin
    glowworm(i).luciferin.x=repmat( luciferin_init , 1 , nVar);
    glowworm(i).luciferin.y=repmat( luciferin_init , 1 , nVar);
    
    %Initialize range 
    glowworm(i).range.x = repmat( range_init , 1 , nVar);
    glowworm(i).range.y = repmat( range_init , 1 , nVar);
 
    neighbors = [];
    % Evaluation
    [glowworm(i).Cost, glowworm(i).Sol]=CostFunction(glowworm(i).Position);
    
    % Update Personal Best
    glowworm(i).Best.Position=glowworm(i).Position;
    glowworm(i).Best.Cost=glowworm(i).Cost;
    glowworm(i).Best.Sol=glowworm(i).Sol;
    
    % Update Global Best
    if glowworm(i).Best.Cost<GlobalBest.Cost
        
        GlobalBest=glowworm(i).Best;
        
    end
end
 
% Array to Hold Best Cost Values at Each Iteration
BestCost=zeros(MaxIt,1);
 
 
for it=1:MaxIt
    
    for i=1:nPop
        
        % x Part
 
    	 % Update luciferin
        %disp(glowworm(i).luciferin.x);
        glowworm(i).luciferin.x = (1-luciferin_decay).*glowworm(i).luciferin.x + luciferin_enhancement.*(glowworm(i).Cost/10);
        %disp(glowworm(i).luciferin.x);
 
        
        for p = 1:nVar
             glowworm(i).range.y(p) = min(range_boundary,max(0.1,glowworm(i).range.y(p) + (beta*(k_neigh-size(neighbors.y,1)))));
        end
        
        %disp(glowworm(i).range.y);
        
           % Evaluation
        [glowworm(i).Cost, glowworm(i).Sol]=CostFunction(glowworm(i).Position);
        
           % Update Personal Best
        if glowworm(i).Cost<glowworm(i).Best.Cost
 
            glowworm(i).Best.Position=glowworm(i).Position;
            glowworm(i).Best.Cost=glowworm(i).Cost;
            glowworm(i).Best.Sol=glowworm(i).Sol;
        end 
        % Update Global Best
        if glowworm(i).Best.Cost<GlobalBest.Cost
            %disp(glowworm(i).luciferin);
            GlobalBest=glowworm(i).Best;
        end
            
        
        
    end
    % Update Best Cost Ever Found
    BestCost(it)=GlobalBest.Cost;
    
     % Show Iteration Information
    if GlobalBest.Sol.IsFeasible
        Flag=' *';
    else
        Flag=[', Violation = ' num2str(GlobalBest.Sol.Violation)];
    end
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it)) Flag]);
    
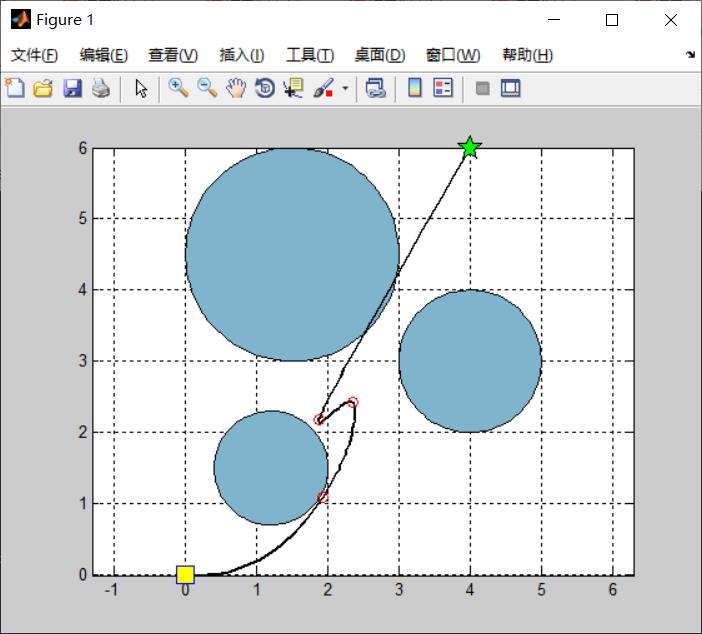
    % Plot Solution
    figure(1);
    PlotSolution(GlobalBest.Sol,model);
    pause(0.01);
end
 
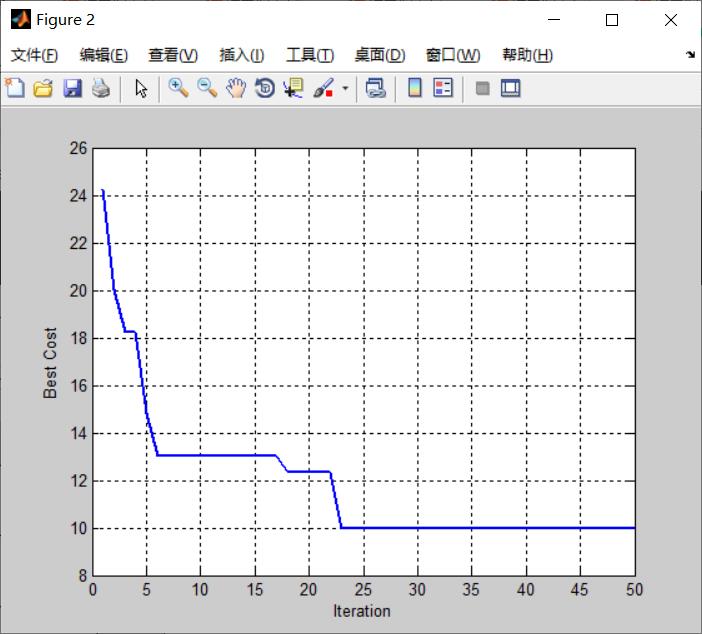
%% Results
 
figure;
plot(BestCost,'LineWidth',2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;
 

完整代码添加QQ1575304183