SVM预测基于蝙蝠算法改进SVM实现数据分类

Posted 2021-06-05 博主QQ2449341593

  最近在学习svm算法，借此文章记录自己的学习过程，在学习很多处借鉴了z老师的讲义和李航的统计，若有不足的地方，请海涵；svm算法通俗的理解在二维上，就是找一分割线把两类分开，问题是如下图三条颜色都可以把点和星划开，但哪条线是最优的呢，这就是我们要考虑的问题；

 

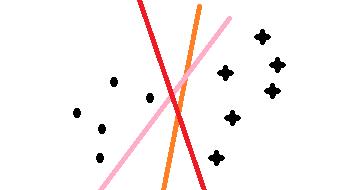
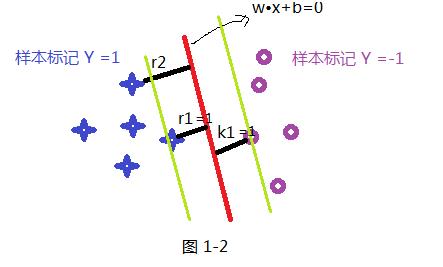
首先我们先假设一条直线为 W•X+b =0 为最优的分割线，把两类分开如下图所示，那我们就要解决的是怎么获取这条最优直线呢?及W 和 b 的值；在SVM中最优分割面(超平面)就是：能使支持向量和超平面最小距离的最大值；

我们的目标是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。

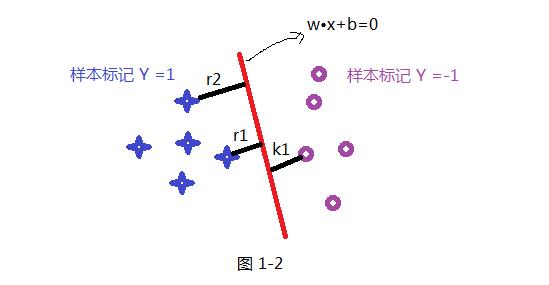
如上面假设蓝色的星星类有5个样本，并设定此类样本标记为Y =1，紫色圈类有5个样本，并设定此类标记为 Y =-1，共 T ={(X₁ ,Y₁) , (X₂,Y₂) (X₃,Y₃) .........} 10个样本，超平面（分割线）为wx+b=0;  样本点到超平面的几何距离为：

     

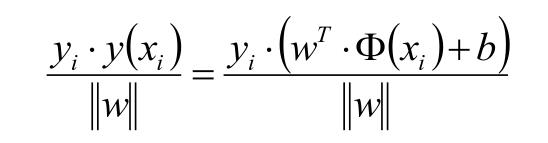
        此处要说明一下：函数距离和几何距离的关系；定义上把 样本| w▪x₁+b|的距离叫做函数距离，而上面公式为几何距离，你会发现当w 和b 同倍数增加时候，函数距离也会通倍数增加；简单个例子就是，样本 X₁ 到 2wX₁+2b =0的函数距离是wX₁ +b =0的函数距离的 2倍；而几何矩阵不变；

        下面我们就要谈谈怎么获取超平面了？！

超平面就是满足支持向量到其最小距离最大，及是求：max [支持向量到超平面的最小距离] ；那只要算出支持向量到超平面的距离就可以了吧 ，而支持向量到超平面的最小距离可以表示如下公式:

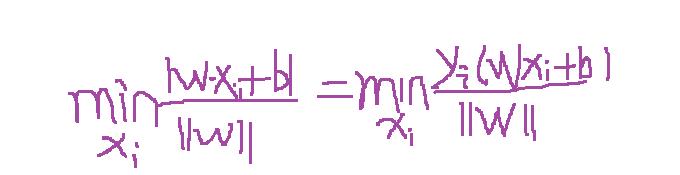
故最终优化的的公式为：

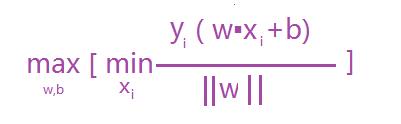
 根据函数距离和几何距离可以得知，w和b增加时候，几何距离不变，故怎能通过同倍数增加w和 b使的支持向量（距离超平面最近的样本点）上样本代入 y(w*x+b) =1,而不影响上面公式的优化，样本点距离如下：如上图其r1函数距离为1，k1函数距离为1,而其它

样本点的函数距离大于1，及是：y(w•x+b)>=1，把此条件代入上面优化公式候，可以获取新的优化公式1-3：

 

公式1-3见下方：优化最大化分数，转化为优化最小化分母，为了优化方便转化为公式1-4

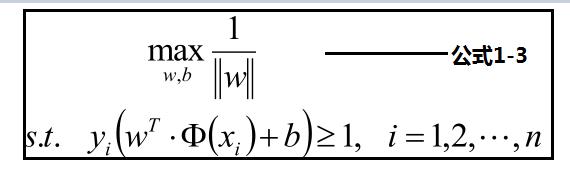
为了优化上面公式，使用拉格朗日公式和KTT条件优化公式转化为：

 

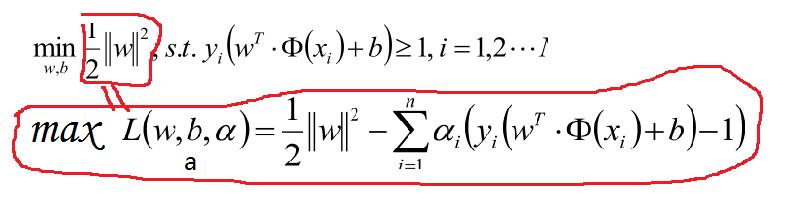
对于上面的优化公式在此说明一下：比如我们的目标问题是 。可以构造函数：

 

 

此时 与 是等价的。因为 ，所以只有在 的情况下

才能取得最大值，因此我们的目标函数可以写为。如果用对偶表达式：，

由于我们的优化是满足强对偶的（强对偶就是说对偶式子的最优值是等于原问题的最优值的），所以在取得最优值 的条件下，它满足 :

，

 

结合上面的一度的对偶说明故我们的优化函数如下面，其中a >0

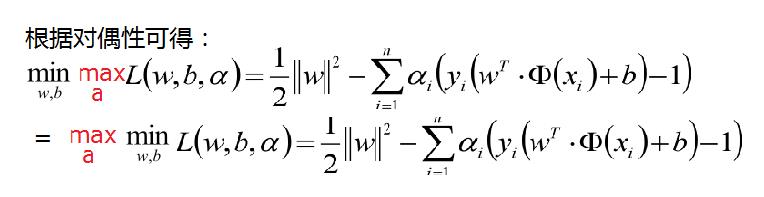
现在的优化方案到上面了，先求最小值，对 w 和 b 分别求偏导可以获取如下公式：

 

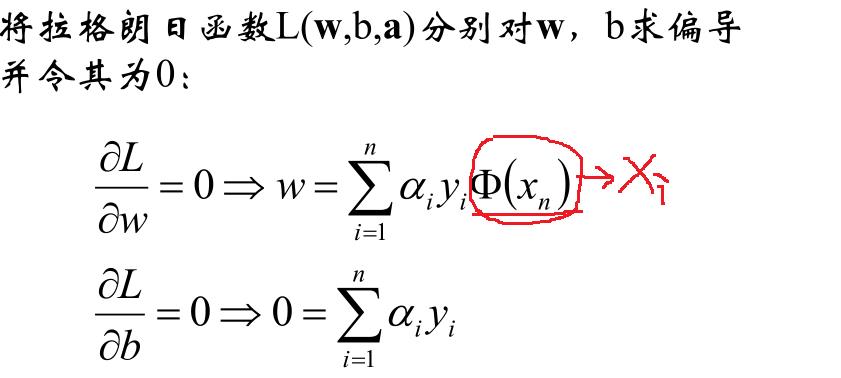
把上式获取的参数代入公式优化max值：

化解到最后一步，就可以获取最优的a值：

以上就可以获取超平面！

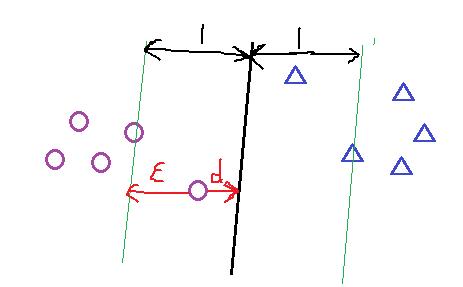
但在正常情况下可能存在一些特异点，将这些特异点去掉后，剩下的大部分点都能线性可分的，有些点线性不可以分，意味着此点的函数距离不是大于等于1，而是小于1的，为了解决这个问题，我们引进了松弛变量 ε>=0; 这样约束条件就会变成为：

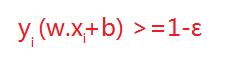
故原先的优化函数变为：

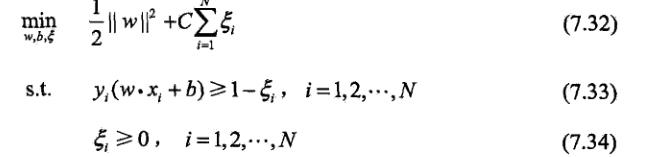
对加入松弛变量后有几点说明如下图所以；距离小于1的样本点离超平面的距离为d ,在绿线和超平面之间的样本点都是由损失的，

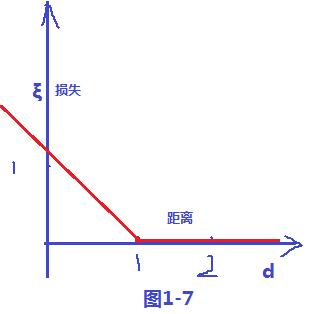
其损失变量和距离d 的关系，可以看出 ξ = 1-d , 当d >1的时候会发现ξ =0，当 d<1 的时候 ξ = 1-d ;故可以画出损失函数图，如下图1-7；样式就像翻书一样，我们把这个损失函数叫做 hinge损失；

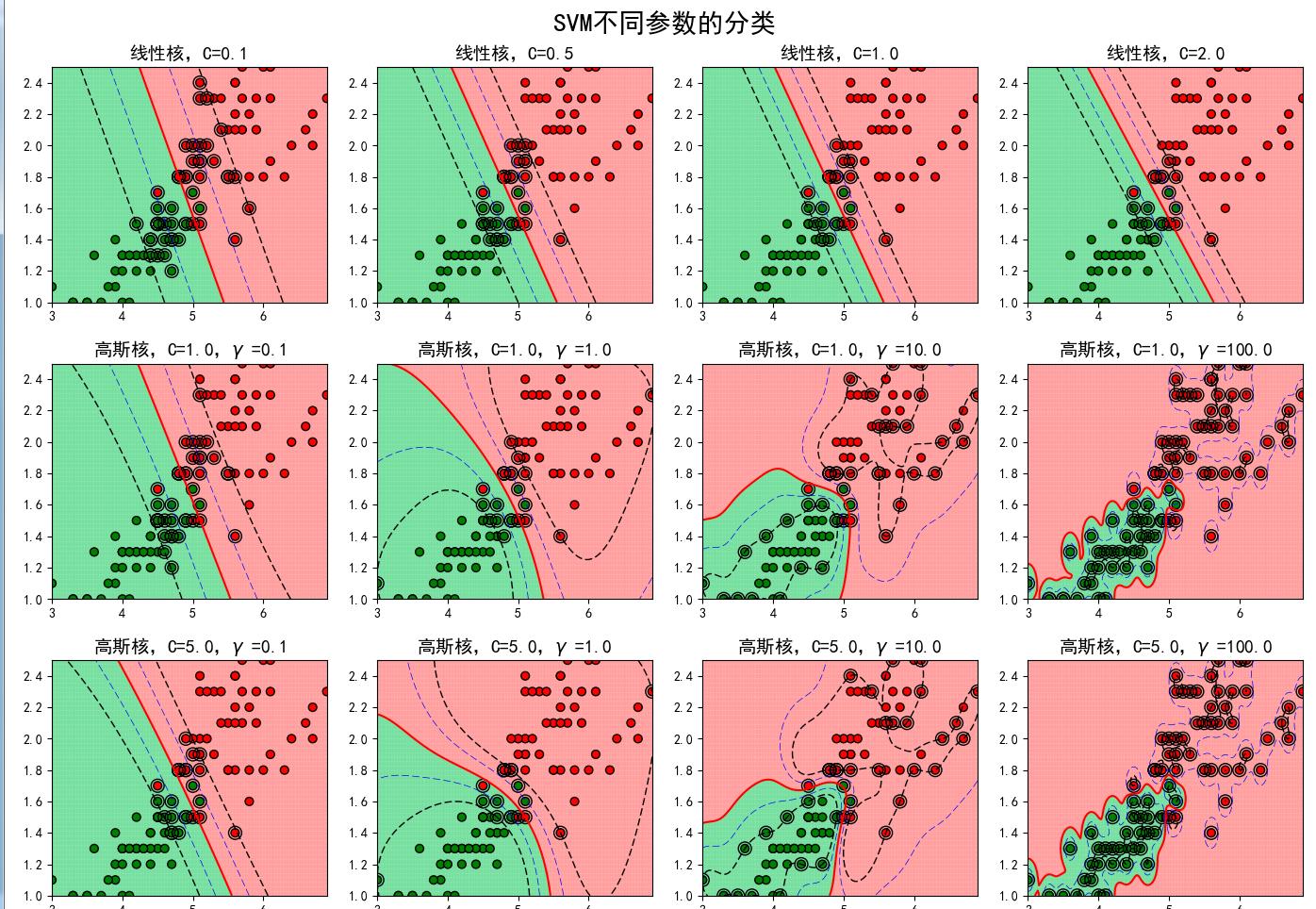
下面我们简单的就来讨论一下核函数：核函数的作用其实很简单就是把低维映射到高维中，便于分类。核函数有高斯核等,下面就直接上图看参数对模型的影响，从下图可以了解，当C变化时候，容错变小，泛化能力变小；当选择高斯核函数的时候，随时R参数调大，准确高提高，最终有过拟合风险；

tic % 计时器
%% 清空环境变量
close all
clear
clc
%format compact
 load('ISSL-Isomap.mat')
%  load CMPE原始
%  mappedX=X;
%% 数据提取
zc=mappedX(1:60,:);%特征输入
lie=mappedX(61:120,:);
mo=mappedX(121:180,:);
que=mappedX(181:240,:);
duan=mappedX(241:300,:);
mm=size(zc,1);
nn=20;
 
a=ones(mm,1);%行为总体样本数
b=2*ones(mm,1);
c=3*ones(mm,1);
d=4*ones(mm,1);
f=5*ones(mm,1);
 
n1=randperm(size(zc,1));
n2=randperm(size(lie,1));
n3=randperm(size(mo,1));
n4=randperm(size(que,1));
n5=randperm(size(duan,1));
 
train_wine = [zc(n1(1:nn),:);lie(n2(1:nn),:);mo(n3(1:nn),:);que(n4(1:nn),:);duan(n5(1:nn),:)];
% 相应的训练集的标签也要分离出来
train_wine_labels = [a(1:nn,:);b(1:nn,:);c(1:nn,:);d(1:nn,:);f(1:nn,:)];
% 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集
test_wine = [zc(n1((nn+1):mm),:);lie(n2((nn+1):mm),:);mo(n3((nn+1):mm),:);que(n4((nn+1):mm),:);duan(n5((nn+1):mm),:)];
% 相应的测试集的标签也要分离出来
test_wine_labels = [a((nn+1):mm,:);b((nn+1):mm,:);c((nn+1):mm,:);d((nn+1):mm,:);f((nn+1):mm,:)];
%% 数据预处理
% 数据预处理,将训练集和测试集归一化到[0,1]区间
[mtrain,ntrain] = size(train_wine);
[mtest,ntest] = size(test_wine);
 
dataset = [train_wine;test_wine];
% mapminmax为MATLAB自带的归一化函数
[dataset_scale,ps] = mapminmax(dataset',0,1);
dataset_scale = dataset_scale';
 
train_wine = dataset_scale(1:mtrain,:);
test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: );
 
 
%% Default parameters 默认参数
 
n=10;      % Population size, typically10 to 40
N_gen=150;  % Number of generations
A=0.5;      % Loudness  (constant or decreasing)
r=0.5;      % Pulse rate (constant or decreasing)
% This frequency range determines the scalings
% You should change these values if necessary
Qmin=0;         % Frequency minimum
Qmax=2;         % Frequency maximum
% Iteration parameters
N_iter=0;       % Total number of function evaluations   %这是什么意思？？？
% Dimension of the search variables
d=2;           % Number of dimensions 
% Lower limit/bounds/ a vector
Lb=[0.01,0.01]; % 参数取值下界
Ub=[100,100]; % 参数取值上界
% Initializing arrays
Q=zeros(n,1);   % Frequency
v=zeros(n,d);   % Velocities
% Initialize the population/solutions
 
% Output/display
disp(['Number of evaluations: ',num2str(N_iter)]);
disp(['Best =',num2str(best),' fmin=',num2str(fmin)]);
 
%% 利用最佳的参数进行SVM网络训练
cmd_gwosvm = ['-c ',num2str(best(:,1)),' -g ',num2str(best(:,2))];
model_gwosvm = svmtrain(train_wine_labels,train_wine,cmd_gwosvm);
%% SVM网络预测
[predict_label] = svmpredict(test_wine_labels,test_wine,model_gwosvm);
total = length(test_wine_labels);% 打印测试集分类准确率
right = length(find(predict_label == test_wine_labels));
Accuracy=right/total;
% disp('打印测试集分类准确率');
% str = sprintf( 'Accuracy = %g%% (%d/%d)',accuracy(1),right,total);
% disp(str);
%% 结果分析
% 测试集的实际分类和预测分类图
figure;
hold on;
plot(test_wine_labels,'o');
plot(predict_label,'r*');
xlabel('测试集样本','FontSize',12);
ylabel('类别标签','FontSize',12);
legend('实际测试集分类','预测测试集分类');
title('测试集的实际分类和预测分类图','FontSize',12);
grid on
snapnow
 
figure
plot(1:N_gen,AAA);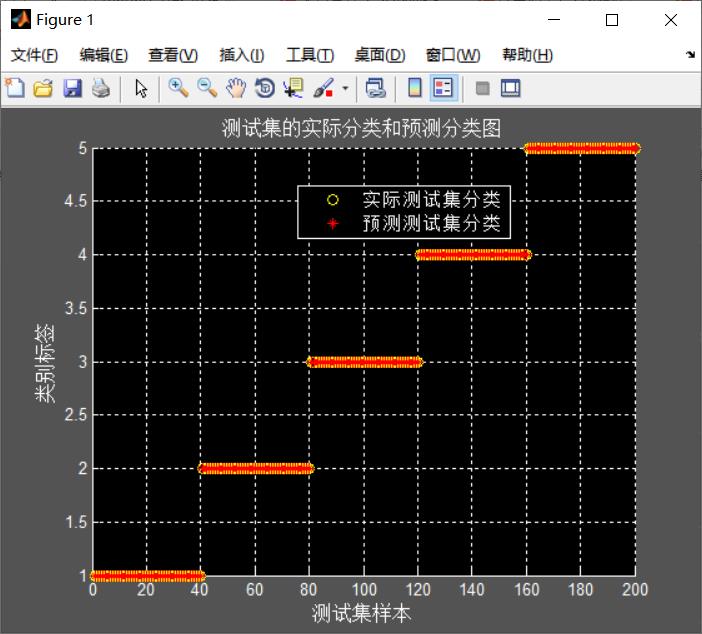

完整代码添加QQ1575304183