TSP问题基于蚁群算法求解带时间窗旅行商问题matlab源码

Posted 2021-06-05 博主QQ2449341593

（一）蚁群算法的由来

蚁群算法最早是由Marco Dorigo等人在1991年提出，他们在研究新型算法的过程中，发现蚁群在寻找食物时，通过分泌一种称为信息素的生物激素交流觅食信息从而能快速的找到目标，据此提出了基于信息正反馈原理的蚁群算法。

 

蚁群算法的基本思想来源于自然界蚂蚁觅食的最短路径原理，根据昆虫科学家的观察，发现自然界的蚂蚁虽然视觉不发达，但它们可以在没有任何提示的情况下找到从食物源到巢穴的最短路径，并在周围环境发生变化后，自适应地搜索新的最佳路径。

 

蚂蚁在寻找食物源的时候，能在其走过的路径上释放一种叫信息素的激素，使一定范围内的其他蚂蚁能够察觉到。当一些路径上通过的蚂蚁越来越多时，信息素也就越来越多，蚂蚁们选择这条路径的概率也就越高，结果导致这条路径上的信息素又增多，蚂蚁走这条路的概率又增加，生生不息。这种选择过程被称为蚂蚁的自催化行为。对于单个蚂蚁来说，它并没有要寻找最短路径，只是根据概率选择；对于整个蚁群系统来说，它们却达到了寻找到最优路径的客观上的效果。这就是群体智能。

 

（二）蚁群算法能做什么

蚁群算法根据模拟蚂蚁寻找食物的最短路径行为来设计的仿生算法，因此一般而言，蚁群算法用来解决最短路径问题，并真的在旅行商问题（TSP，一个寻找最短路径的问题）上取得了比较好的成效。目前，也已渐渐应用到其他领域中去，在图着色问题、车辆调度问题、集成电路设计、通讯网络、数据聚类分析等方面都有所应用。

 

（三）蚁群算法的流程步骤

 

这里以TSP问题为例，算法设计的流程如下：

步骤1：对相关参数进行初始化，包括蚁群规模、信息素因子、启发函数因子、信息素挥发因子、信息素常数、最大迭代次数等，以及将数据读入程序，并进行预处理：比如将城市的坐标信息转换为城市间的距离矩阵。
步骤2：随机将蚂蚁放于不同出发点，对每个蚂蚁计算其下个访问城市，直到有蚂蚁访问完所有城市。
步骤3：计算各蚂蚁经过的路径长度Lk，记录当前迭代次数最优解，同时对路径上的信息素浓度进行更新。
步骤4：判断是否达到最大迭代次数，若否，返回步骤2；是，结束程序。
步骤5：输出结果，并根据需要输出寻优过程中的相关指标，如运行时间、收敛迭代次数等。

 

要用到的符号说明：

m：整个蚂蚁群体中蚂蚁数量；
n：城市的数量；
dij：城市i与城市j的距离
βij(t)：t时刻城市i和城市j连接路径上的信息素；
pkij(t)：t时刻蚂蚁k从城市i转移到城市j的概率；

初始时刻蚂蚁被放在不同的城市，且各城市路径上的信息素浓度为0。

 

由于蚁群算法涉及到的参数蛮多的，且这些参数的选择对程序又都有一定的影响，所以选择合适的参数组合很重要。蚁群算法有个特点就是在寻优的过程中，带有一定的随机性，这种随机性主要体现在出发点的选择上。蚁群算法正是通过这个初始点的选择将全局寻优慢慢转化为局部寻优的。参数设定的关键就在于在“全局”和“局部”之间建立一个平衡点。

 

（四）蚁群算法的关键参数

在蚁群算法的发展中，关键参数的设定有一定的准则，一般来讲遵循以下几条：

 

1.尽可能在全局上搜索最优解，保证解的最优性；
2.算法尽快收敛，以节省寻优时间；
3.尽量反应客观存在的规律，以保证这类仿生算法的真实性。

 

蚁群算法中主要有下面几个参数需要设定：

蚂蚁数量：
设M表示城市数量，m表示蚂蚁数量。m的数量很重要，因为m过大时，会导致搜索过的路径上信息素变化趋于平均，这样就不好找出好的路径了；m过小时，易使未被搜索到的路径信息素减小到0，这样可能会出现早熟，没找到全局最优解。一般上，在时间等资源条件紧迫的情况下，蚂蚁数设定为城市数的1.5倍较稳妥。

 

信息素因子：
信息素因子反映了蚂蚁在移动过程中所积累的信息量在指导蚁群搜索中的相对重要程度，其值过大，蚂蚁选择以前走过的路径概率大，搜索随机性减弱；值过小，等同于贪婪算法，使搜索过早陷入局部最优。实验发现，信息素因子选择[1,4]区间，性能较好。

 

启发函数因子：
启发函数因子反映了启发式信息在指导蚁群搜索过程中的相对重要程度，其大小反映的是蚁群寻优过程中先验性和确定性因素的作用强度。过大时，虽然收敛速度会加快，但容易陷入局部最优；过小时，容易陷入随机搜索，找不到最优解。实验研究发现，当启发函数因子为[3,4.5]时，综合求解性能较好。

 

信息素挥发因子：
信息素挥发因子表示信息素的消失水平，它的大小直接关系到蚁群算法的全局搜索能力和收敛速度。实验发现，当属于[0.2，0.5]时,综合性能较好。

 

信息素常数：
这个参数为信息素强度，表示蚂蚁循环一周时释放在路径上的信息素总量，其作用是为了充分利用有向图上的全局信息反馈量，使算法在正反馈机制作用下以合理的演化速度搜索到全局最优解。值越大，蚂蚁在已遍历路径上的信息素积累越快，有助于快速收敛。实验发现，当值属于[10,1000]时，综合性能较好。

 

最大迭代次数：
最大迭代次数值过小，可能导致算法还没收敛就已结束；过大则会导致资源浪费。一般最大迭代次数可以取100到500次。一般来讲，建议先取200，然后根据执行程序查看算法收敛的轨迹来修改取值。

clear
clc
close all
tic
%% 用importdata这个函数来读取文件

Dta=importdata('c102.txt');
c101=Dta.data;
%% 提取数据信息
E=c101(1,5);                                                    %配送中心时间窗开始时间
L=c101(1,6);                                                    %配送中心时间窗结束时间
vertexs=c101(:,2:3);                                            %所有点的坐标x和y
% vertexs1=c101(:,2:3);                                            %所有点的坐标x和y
for i=1:size(vertexs,1)
    [vertexs(i,2),vertexs(i,1)]=jingwei(vertexs(i,2),vertexs(i,1));
end
customer=vertexs(2:end,:);                                      %顾客坐标
cusnum=size(customer,1);                                        %顾客数
v_num=1;                                                       %车辆最多使用数目
% demands=1*c101(2:end,4);                                          %需求量
a=c101(2:end,5);                                                %顾客时间窗开始时间[a[i],b[i]]
b=c101(2:end,6);                                                %顾客时间窗结束时间[a[i],b[i]]
width=b-a;                                                      %顾客的时间窗宽度
s=c101(2:end,4);                                                %客户点的服务时间
h=pdist(vertexs);
dist=squareform(h);                                             %距离矩阵
%% 初始化参数
m=60;                                                           %蚂蚁数量
alpha=1;                                                        %信息素重要程度因子
beta=3;                                                         %启发函数重要程度因子
gama=2;                                                         %等待时间重要程度因子
delta=3;                                                        %时间窗跨度重要程度因子
r0=0.5;                                                         %r0为用来控制转移规则的参数

  
end
%% 改进蚁群结果显示
bestRoute=Route_best(end,:);
[bestVC,NV,TD]=decode(bestRoute,a,b,L,s,dist);
figure
hold on;box on
title('蚁群最优配送方案路线图')
hold on;
disp('蚁群路径方案')
  disp(['车辆行驶总距离：',num2str(bestTD)]);
    disp(['最佳适应度值：',num2str(min(Cost_best))]);
draw_Best(bestVC,vertexs);

%% 绘图
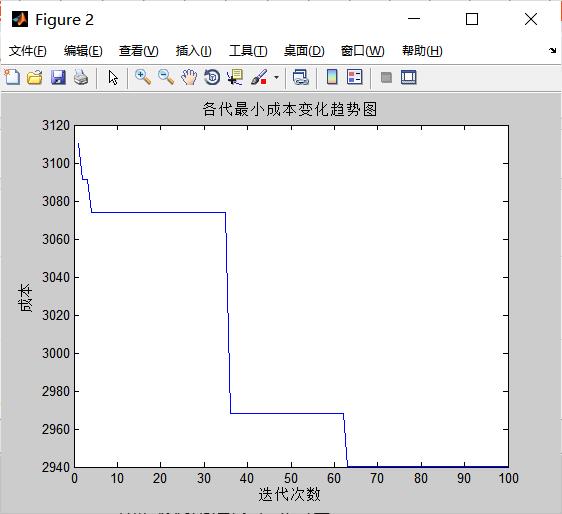
figure
plot(1:iter_max,Cost_best,'b')
xlabel('迭代次数')
ylabel('成本')
title('各代最小成本变化趋势图')
toc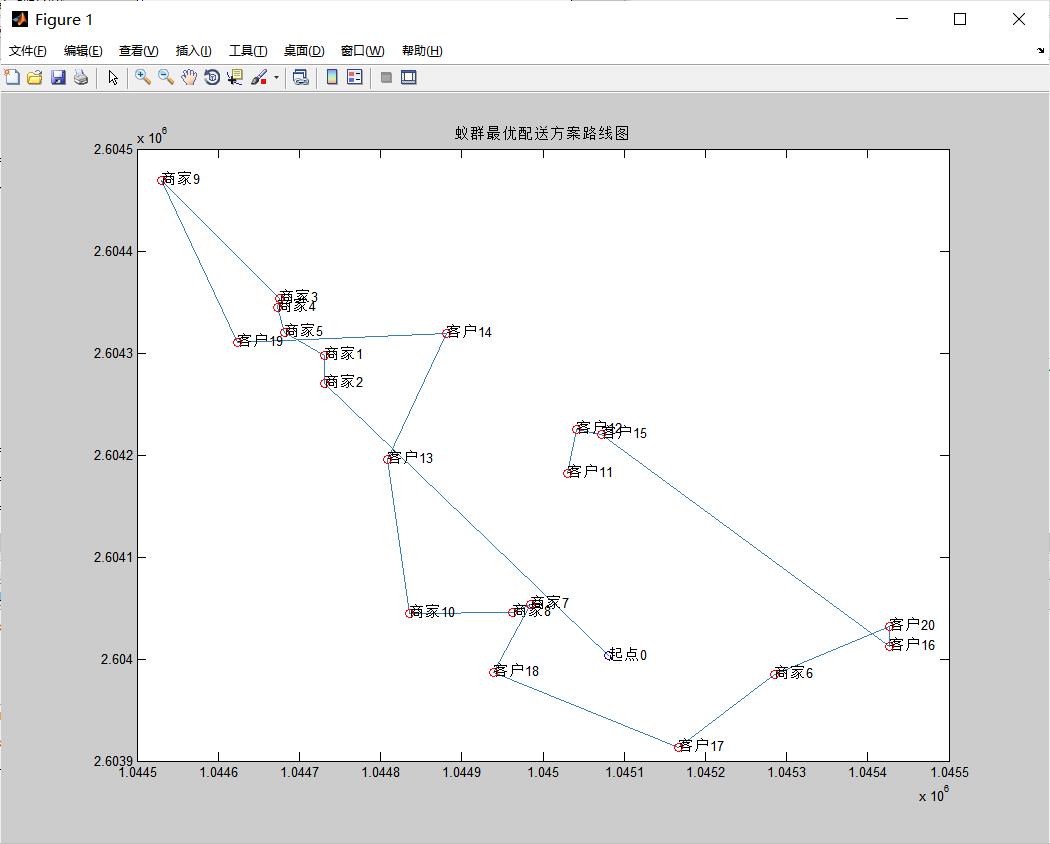

完整代码或者仿真咨询添加QQ1575304183