坐标系与DCM旋转矩阵
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了坐标系与DCM旋转矩阵相关的知识,希望对你有一定的参考价值。
参考技术A 导航坐标系 常用的导航坐标系有 北东地(NED) 和 东北天(ENU) 两种。他们的指向定义分别如下:北东地(ENU)坐标系 东北天(NED)坐标系
X→北 X→东
Y→东 Y→北
Z→地 Z→天
载体坐标系 与导航坐标系类似,常用的也有如下两种:
前右下坐标系-北东地坐标系 右前上坐标系- 东北天坐标系
X→前 X→右
Y→右 Y→前
Z→下 Z→上
首先要明确旋转在二维中是绕着某一个点进行旋转,三维中是绕着某一个轴进行旋转。二维旋转中最简单的场景是绕着坐标原点进行的旋转,如下图所示:
如图所示点v 绕 原点旋转θθ 角,得到点v’,假设 v点的坐标是(x, y) ,那么可以推导得到 v’点的坐标(x’, y’)(设原点到v的距离是r,原点到v点的向量与x轴的夹角是ϕϕ )
通过三角函数展开:
代入x、y表达式:
写成矩阵的形式:
本文采用右手坐标系,同时旋转角度的正负也遵循右手坐标系的约定。
旋转顺序依次为 Z - Y - X。
绕 Z 轴的旋转矩阵:
绕 Y 轴的旋转矩阵:
绕 X 轴的旋转矩阵:
将以上矩阵按照Z-Y-X的转动顺序连乘,可以求得一个可以表示这个欧拉转动的旋转矩阵,也被称之为方向余弦矩阵。
绕 Z 轴的旋转矩阵:
绕 Y 轴的旋转矩阵:
绕 X 轴的旋转矩阵:
则:
记
则
roll :
pitch :
yaw:
变换矩阵
一.坐标变换:缩放、平移、旋转
1.缩放
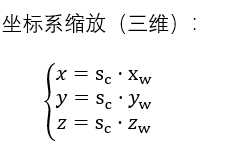
其中Sc是缩放比例
2.平移
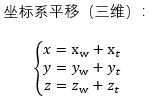
3.旋转
3.1二维坐标系旋转

3.2三维坐标系旋转
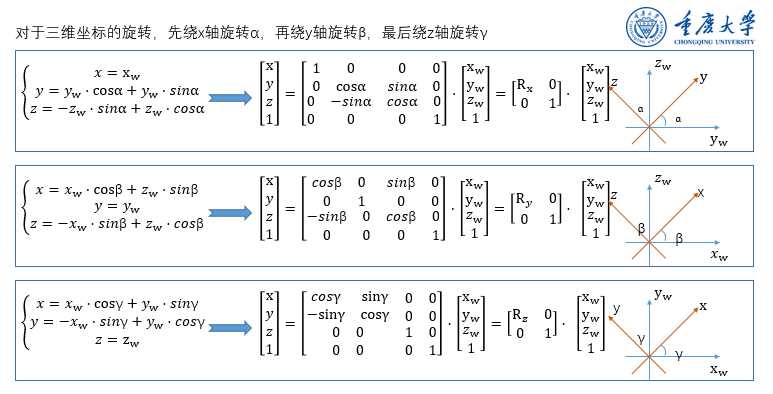

二.向量变换(旋转、平移)
1.向量

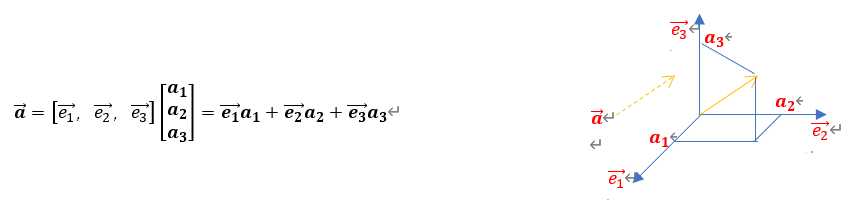
2.向量的内积

3.向量的外积

4.向量的性质补充

5.向量的旋转
向量的旋转与向量的外积(叉乘):旋转轴方向与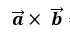 一致。旋转的角度
一致。旋转的角度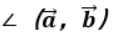
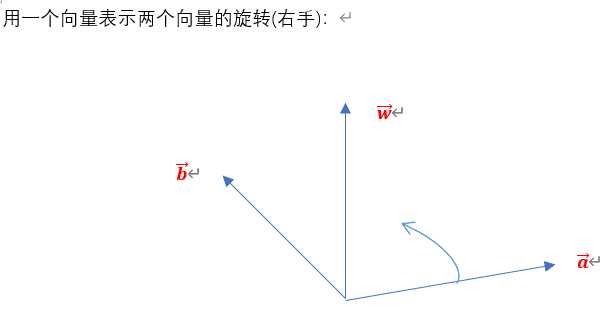
6.坐标系的旋转
三维直角坐标系的三个轴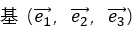 的相对位置永远保持一致(刚体),只需要对一个向量如:
的相对位置永远保持一致(刚体),只需要对一个向量如: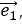 旋转平移,整个坐标系就完成了变换操作
旋转平移,整个坐标系就完成了变换操作
6.1刚体的变换(坐标系的欧式变换)
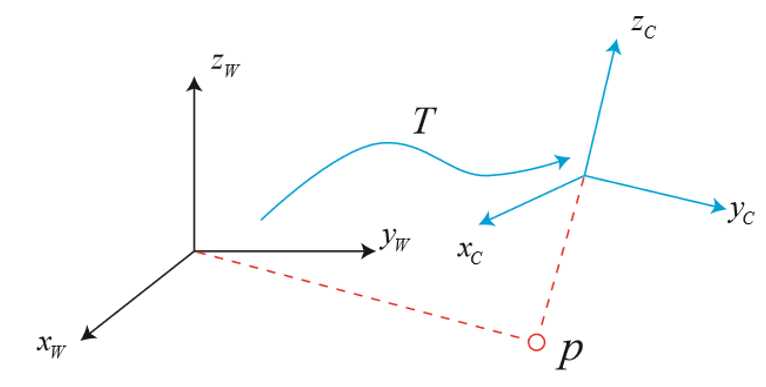




以上是关于坐标系与DCM旋转矩阵的主要内容,如果未能解决你的问题,请参考以下文章