图像去噪基于KSVD实现图像去噪matlab源码

Posted 2021-06-05 博主QQ2449341593

 

1.引言

 

 　　稀疏编码以成功应用于计算机视觉和图像分析中的各种问题，包括图像降噪，图像恢复，图像分类。稀疏编码接近于一个输入信号，Υ是过完备字典D中原子的稀疏编码线性组合。稀疏编码的性能依赖于字典D的质量。[28]利用全部的训练样本作为判决稀疏编码的字典，在人脸识别上实现了较好的性能。很多算法提出高效率的学习一个过完备字典以增强判决标准。

　　为了扩展到大型训练集，[28,19,1,24,33,6]发展了小型字典学习。在[28]中手动选择训练样本来构建字典。[19]为每个类学习一个单独的字典，然后根据重构错误执行分类。然而，在有很多类别时，训练期间的字典重建和测试阶段的稀疏编码是典型的非常耗时。在[1]中，字典学习算法k-svd，提出了从一组训练信号中高效的学习过完备字典。该方法已用于填补像素和图像压缩。K-SVD侧重于已学习到的字典中的表示能力（训练信号的最佳稀疏表示），没有考虑字典的判决能力。最优方向方法（mod）与K-SVD有相同的有效稀疏编码。[24]通过基于线性预测分类器的结果迭代更新字典项来获得一个判决字典。在[33]中，提出的判决K-SVD算法统一了字典和分类器的学习过程。

　　本文提出了一种有监督的算法来学习一个小型的判决字典用于稀疏编码。明确的将判决稀疏编码错误准则和最优的分类准则合并到目标函数中，并使用K-SVD算法对其进行优化。学习到的字典与传统构造字典相比，具有重构性和判决性，学习的字典提供信号的判决稀疏表示。因此，即使使用多类线性分类器，也能得到在物体分类时得到较好的准确率，现有的其他稀疏编码方法，对每一类别只学习一个分类器。我们的方法是有效的，并受到k-svd的复杂性限制，同时学习判决字典和线性分类器。[30,20]迭代的解决子问题以近似一个联合解，[13,3,19,21]分别学习字典和分类器。

1.1 相关工作

　　近年来，用于稀疏编码的有监督字典学习技术受到了广泛关注。一些方法学习多个字典或特定于类别的字典。[34,31]将一个增强过程纳入字典学习中，学习具有互补能力的多个字典。【19】中一个类学习一个字典，基于相应的重构误差进行分类，并没有利用稀疏编码。

　　在训练阶段将判决项纳入目标函数已经在【30,20,33,19,21,24,3,13】中提出。判决标准包括：softmax判决代价函数，Fisher判决准则，线性预测分类错误，hinge损失函数。

　　大多数以前的方法将字典学习和分类器训练视为两个独立的过程。在这些方法中，常常先学到一个字典，然后基于这个字典训练分类器。得到分类器后，稀疏表示作为用分类器训练的图像特征，例如SVM。更复杂的方法将这两个过程统一为一个混合的重建和判决公式。我们的方法也属于这一类。【30,20】同时为 每一类同步学习一个过完备字典和多类分类模型，可能不能很好地扩展到含有大量的类别中，【24】中的方法基于线性分类器的结果迭代更新字典，可能会引起局部最小化问题，因为它在字典重建和分类设计中交替。【33】将分类错误纳入目标函数，但是并没有保证利用小型字典时稀疏编码的判决性。

　　本文的方法：同时学习一个单一的小型的判决字典和一个通用的多类线性分类器（为所有的类）学习到的字典具有很好的表示能力（跨越对象类的所有子空间），并对所有类实施更好的识别能力。

 

2 字典学习

 

2.1 字典学习用于重建和稀疏编码

　　Y表示一组N个输入信号n维 Y = [y1...yN]∈Rn×N,学习一个具有k个原子的重建字典用于Y的稀疏表示：

 ，（过完备字典），是输入信号Y的稀疏编码。T是稀疏约束项，（每个信号在分解后都少于T个原子），||Y-DX||22表示重建误差。通过最小化重构误差和满足稀疏约束来实现D的构造。K-SVD算法是一种最小化方程1能量的迭代方法，学习一个用于信号稀疏表示的重建字典。该方法效率高，适用于图像复原和压缩等领域。根据D，Y的稀疏编码X：

 

2.2 字典学习用于分类

　　稀疏编码x可以直接的作为特征进行分类。通过模型参数W∈Rm×K，可以得到一个好的分类器。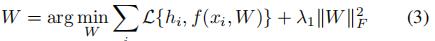

 ：分类损失函数，hi是yi的标签，λ1：正则参数。字典学习和分类器分离可能使D成为分类的次优选择，联合学习字典和分类模型，尝试优化用于分类任务的学习字典，结合字典D和w的目标函数定义为：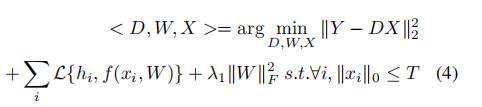

 

　　这些方法需要学习相对较大的字典来获得较好的分类性能，导致计算量较大。当只能基于多个两两分类器的分类体系结构来获得好的分类结果时，这个问题会变得更加严重。

·　　通过联合字典和分类器构造的目标函数的简单扩展，我们将证明仅使用一个小的单一的统一字典来得到良好的分类结果。这个扩展强制了一个标签一致性约束在字典上-直观的说，字典元素在分类过程中贡献的类分布在一个类中达到了顶峰。这个方法时LC-KSVD,利用了原始的K-SVD求解。

3 Label Consistent K-SVD

　　目标是利用输入信号的有监督信息学习一个重建的和判决字典。每个字典项都将被选中，这样它就代表了训练信号的一个子集，理想情况下来自单个类，因此，每一个字典项都可以与特征的标签相关联。因此，在我们的方法中，字典项和标签之间有明确的对应关系。

　　在方程1的目标函数中加入标签一致性正则项，联合分类错误误差和标签一致性正则项对学习具有更平衡的重构能力和辨别能力的词典的影响。分别称他们为 LC-KSVD1和LC-KSVD2.

3.1 LC-KSVD1

　　线性分类器的性能依赖于输入的稀疏编码x的判别性，对于用D得到的可判别性稀疏编码x，用于字典构建的目标函数定义为：

 

 其中α是是控制重建和标签一致正则化之间的相对贡献。Q = [q1...qN]∈RK×N是用于分类的输入信号Y的判决稀疏编码。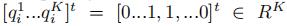是和输入信息yi相对应的稀疏编码，条件是qi的非零值出现在输入信号yi和字典项dk共享相同标签的索引处。A是一个线性转换矩阵。定义的转换函数，g(x; A) = Ax,将原始的稀疏编码x在稀疏特征空间中更具判决性

　　

表示判决稀疏编码误差，强使稀疏编码X接近判决稀疏编码Q。它使来自下相同类的信号有非常相似的稀疏表示，利用简单分类器就能取得好的分类性能。

 

 3.2 LC-KSVD2

　　为了使分类最优，将分类错误作为一项添加到目标函数中。在此利用了一个线性预测分类器 f(x;W) = Wx.目标函数用于学习一个具有重建和判别能力的字典D。定义如下：

表示分类误差，W表示分类器参数。H=[h1...hN ]∈Rm×N是输入信号Y的类标签。hi = [0,0..1...0,0]∈Rm 是yi相应的标签向量，非零位置表示yi的类别，α和β是是控制相应项的相对贡献。

　　假设判决稀疏编码X' = AX ， A∈RK×K，D' = DA-1,W'=WT-1，（wx = w'x'，W'应该为WA-1）公式6重写为

 

 第一项是重建误差，第二项是判决稀疏编码误差，第三项是分类误差。

　　这种方式学习的字典与训练数据的底层结构相适应，不管字典的大小，都将生成有区别的稀疏编码X，这些稀疏编码可以被分类器直接利用。稀疏编码x的判别性质对线性分类器的性质非常重要。

　　优化过程：LC-KSVD1 ,LC-KSVD2采用相同的方法，LCKSVD1将方程8和14中的H,W分类排除在外。在训练过程中，首先由公式5计算D,A,X，然后利用公式14对矩阵W进行分类训练。

3.3 优化

　　利用有效的K-SVD算法对所有的参数进行优化。方式6重写为

xRk:X的第k行，

 

 

 D,A,W同步，避免了局部最小化。

 3.3.1 初始化 LC-KSVD

　　对于d0，我们在每个类中使用几个k-svd迭代，然后合并每个k-svd的所有输出（即从每个类学习的字典项）。然后，每个字典项dk的标签根据其对应的类初始化，并且在1700整个字典学习过程1中保持固定，尽管dk在学习过程中被更新。字典元素被统一地分配给每个类，元素的数量与字典的大小成比例。A0采用了多元岭回归模型，二次方损失，L2范数正则。

3.4 分类方法

D = {d1,...dk},A = {a1,...ak},

 4.实验

　　扩展YaleB和AR数据集中使用的特征描述符是任意的人脸，将一张人脸投影到一个随机向量生成的。扩展YaleB是504维，AR是540维。Caltech101数据集，首先从16*16的块中提取sift描述符，是由步长6像素大小的网格密采样得到的，然后再提取sift的基础上，采用1*1,2*2,4*4的网格提取空间金字塔特征。为了训练金字塔的码本，我们使用k=1024的标准k-means聚类。最后将空间金字塔降至3000维。

　　在空间金字塔的每个空间子区域中，矢量量化码被汇集在一起以形成汇集特征。这些来自每个子区域的集合特征被连接并规范化为图像的最终空间金字塔特征。caltech101数据集的稀疏代码是根据空间金字塔特征计算的。这有两种池方法：和池化：xout = x1+, ..., +xn，最大池化：xout = max(x1, ..., xn)，xi是矢量量化码。这些特征归一化：

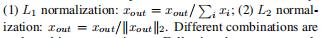，我们的实验评估了不同的组合。按照常用的评价方法，对训练图像和测试图像进行10次不同随机的重复实验，以获得可靠的结果。最终识别率报告为每次运行的平均值。我们所有实验中使用的稀疏因子是30。

%============================================================
%               demo2 - denoise an image
% this is a run_file the demonstrate how to denoise an image, 
% using dictionaries. The methods implemented here are the same
% one as described in "Image Denoising Via Sparse and Redundant
% representations over Learned Dictionaries", (appeared in the 
% IEEE Trans. on Image Processing, Vol. 15, no. 12, December 2006).
%============================================================

clear
bb=8; % block size
RR=4; % redundancy factor
K=RR*bb^2; % number of atoms in the dictionary

sigma = 25; 
pathForImages ='';
imageName = 'BJ200_14.BMP';
[IMin0,pp]=imread(strcat([pathForImages,imageName]));
IMin0=im2double(IMin0);
if (length(size(IMin0))>2)
    IMin0 = rgb2gray(IMin0);
end
if (max(IMin0(:))<2)
    IMin0 = IMin0*255;
end

IMin=IMin0+sigma*randn(size(IMin0));
PSNRIn = 20*log10(255/sqrt(mean((IMin(:)-IMin0(:)).^2)));
%==========================================================================
%   P E R F O R M   D E N O I S I N G   U S I N G   O V E R C O M P L E T E 
%                        D C T    D I C T I O N A R Y
%==========================================================================
tic
[IoutDCT,output] = denoiseImageDCT(IMin, sigma, K);

PSNROut = 20*log10(255/sqrt(mean((IoutDCT(:)-IMin0(:)).^2)));
figure;
%subplot(1,3,1); imshow(IMin0,[]); title('Original clean image');
%subplot(1,3,2); imshow(IMin,[]); title(strcat(['Noisy image, ',num2str(PSNRIn),'dB']));
%subplot(1,3,3); 
imshow(IoutDCT,[]); title(strcat(['Clean Image by DCT dictionary, ',num2str(PSNROut),'dB']));
figure;
I = displayDictionaryElementsAsImage(output.D, floor(sqrt(K)), floor(size(output.D,2)/floor(sqrt(K))),bb,bb,0);
title('The DCT dictionary');
toc
%==========================================================================
%   P E R F O R M   D E N O I S I N G   U S I N G   G L O B A L 
%           ( O R   G I V E N )   D I C T I O N A R Y
%==========================================================================
tic
[IoutGlobal,output] = denoiseImageGlobal(IMin, sigma,K);

PSNROut = 20*log10(255/sqrt(mean((IoutGlobal(:)-IMin0(:)).^2)));
figure;
%subplot(1,3,1); imshow(IMin0,[]); title('Original clean image');
%subplot(1,3,2); imshow(IMin,[]); title(strcat(['Noisy image, ',num2str(PSNRIn),'dB']));
%subplot(1,3,3);
imshow(IoutGlobal,[]); title(strcat(['Clean Image by Global Trained dictionary, ',num2str(PSNROut),'dB']));
figure;
I = displayDictionaryElementsAsImage(output.D, floor(sqrt(K)), floor(size(output.D,2)/floor(sqrt(K))),bb,bb);
title('The dictionary trained on patches from natural images');
toc

%==========================================================================
%   P E R F O R M   D E N O I S I N G   U S I N G   A   D I C T  I O N A R Y
%                  T R A I N E D   O N   N O I S Y   I M A G E
%==========================================================================
tic
[IoutAdaptive,output] = denoiseImageKSVD(IMin, sigma,K);

PSNROut = 20*log10(255/sqrt(mean((IoutAdaptive(:)-IMin0(:)).^2)));
figure;
subplot(1,3,1); imshow(IMin0,[]); title('Original clean image');
subplot(1,3,2); imshow(IMin,[]); title(strcat(['Noisy image, ',num2str(PSNRIn),'dB']));
subplot(1,3,3); imshow(IoutAdaptive,[]); title(strcat(['Clean Image by Adaptive dictionary, ',num2str(PSNROut),'dB']));

figure;
I = displayDictionaryElementsAsImage(output.D, floor(sqrt(K)), floor(size(output.D,2)/floor(sqrt(K))),bb,bb);
title('The dictionary trained on patches from the noisy image');
toc

完整代码或者仿真咨询添加QQ1575304183