leetcode 11. 盛最多水的容器----双指针篇2

Posted 2021-06-04 大忽悠爱忽悠

盛水最多的容器题解集合

• 暴力法
• 双指针法

---

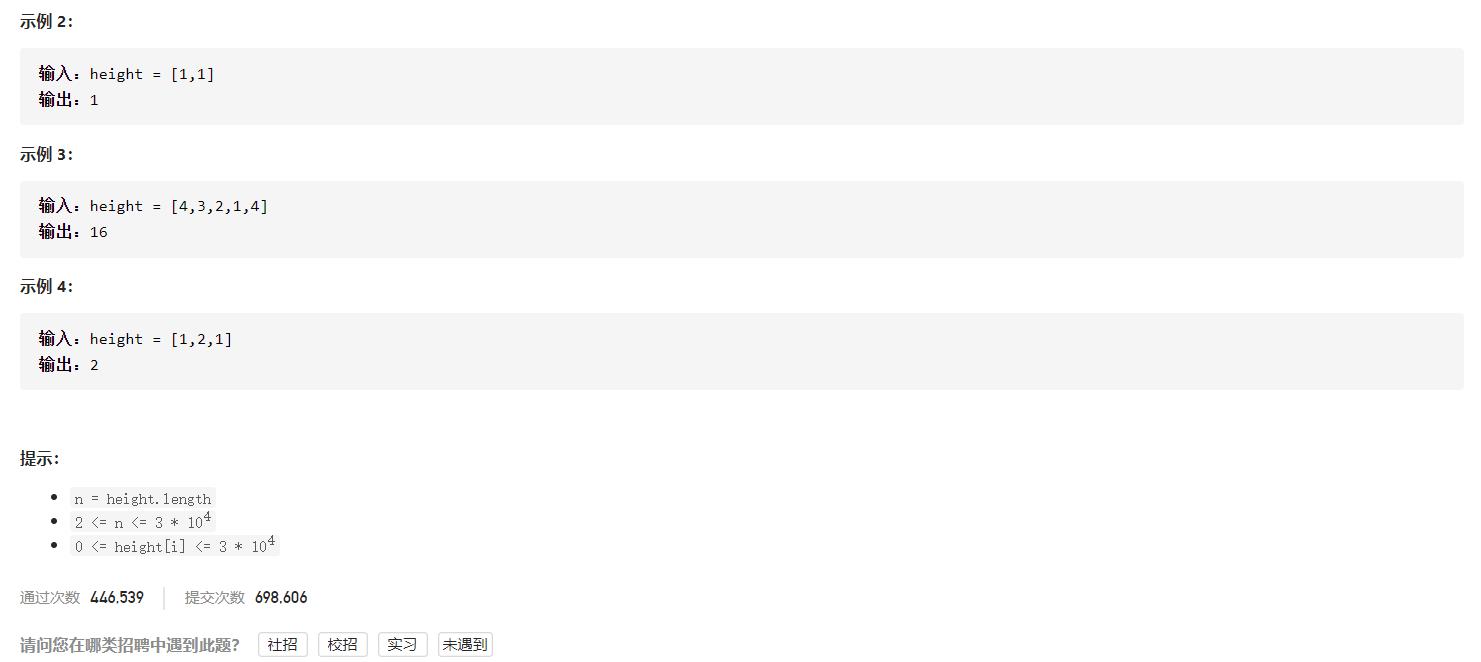
暴力法

思路:

双重for循环列举出所有可能答案，找出其中的最大结果

class Solution {
public:
	int maxArea(vector<int>& height)
	{
		int maxArea = 0;
		for (int i = 0; i < height.size(); i++)
		{
			for (int j = 1; j < height.size(); j++)
				maxArea = max(maxArea, (j - i) * min(height[i], height[j]));
		}
		return maxArea;
	}
};

---

双指针法

思路:
设置双指针 i,j 分别位于容器壁两端，根据规则移动指针（后续说明），并且更新面积最大值 res，直到 i == j 时返回 res。

指针移动规则:

每次选定围成水槽两板高度 h[i],h[j] 中的短板，向中间收窄 1 格。

• 设每一状态下水槽面积为 S(i, j),(0<=i<j<n)，由于水槽的实际高度由两板中的短板决定，则可得面积公式 S(i, j) = min(h[i], h[j]) × (j - i)。

• 在每一个状态下，无论长板或短板收窄 1 格，都会导致水槽 底边宽度 -1：

• 若向内移动短板，水槽的短板 min(h[i], h[j])可能变大，因此水槽面积 S(i, j)可能增大。

• 若向内移动长板，水槽的短板 min(h[i], h[j])不变或变小，下个水槽的面积一定小于当前水槽面积。

• 因此，向内收窄短板可以获取面积最大值。

复杂度分析：

• 时间复杂度 O(N)，双指针遍历一次底边宽度 N 。
• 空间复杂度 O(1)，指针使用常数额外空间。

图解:

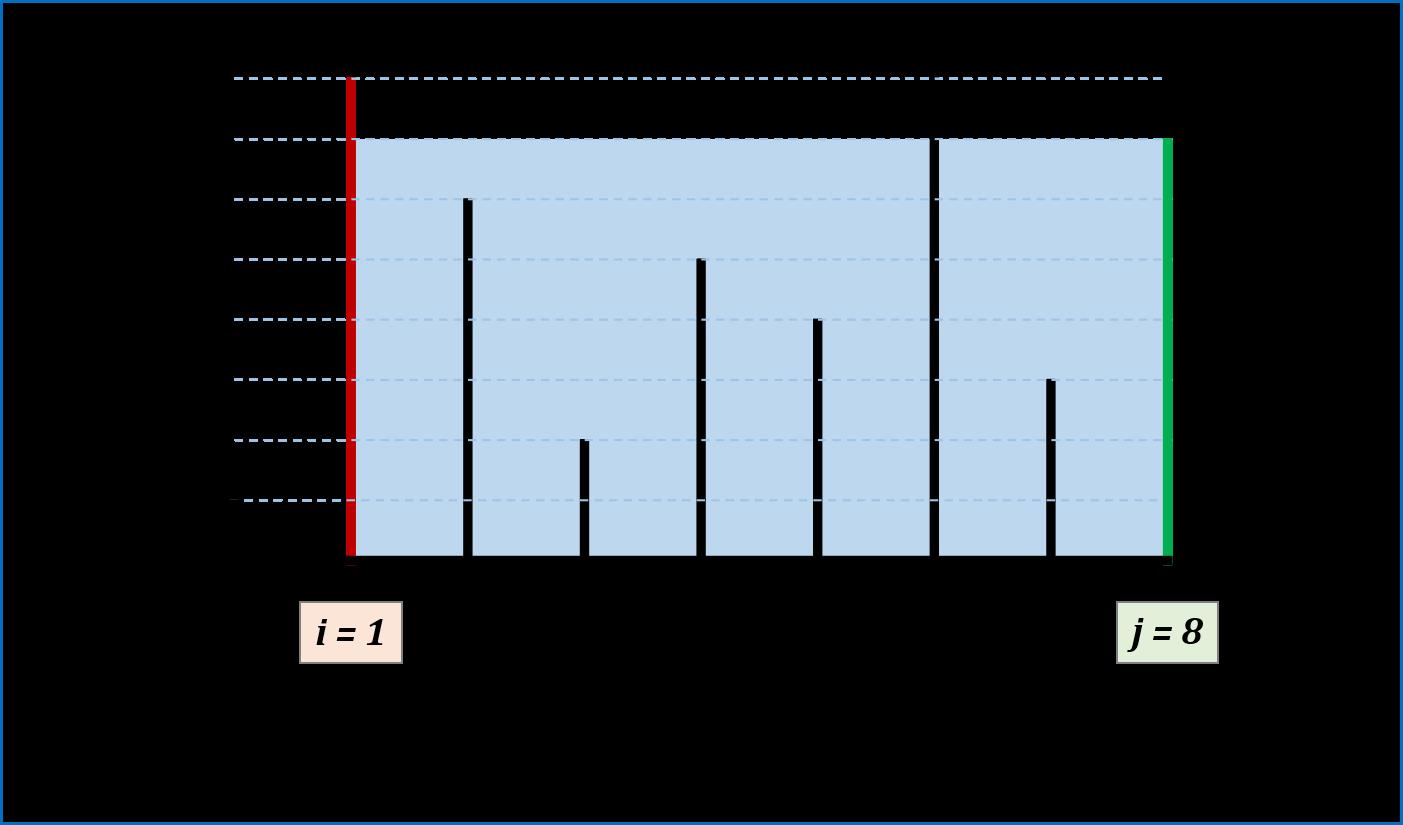
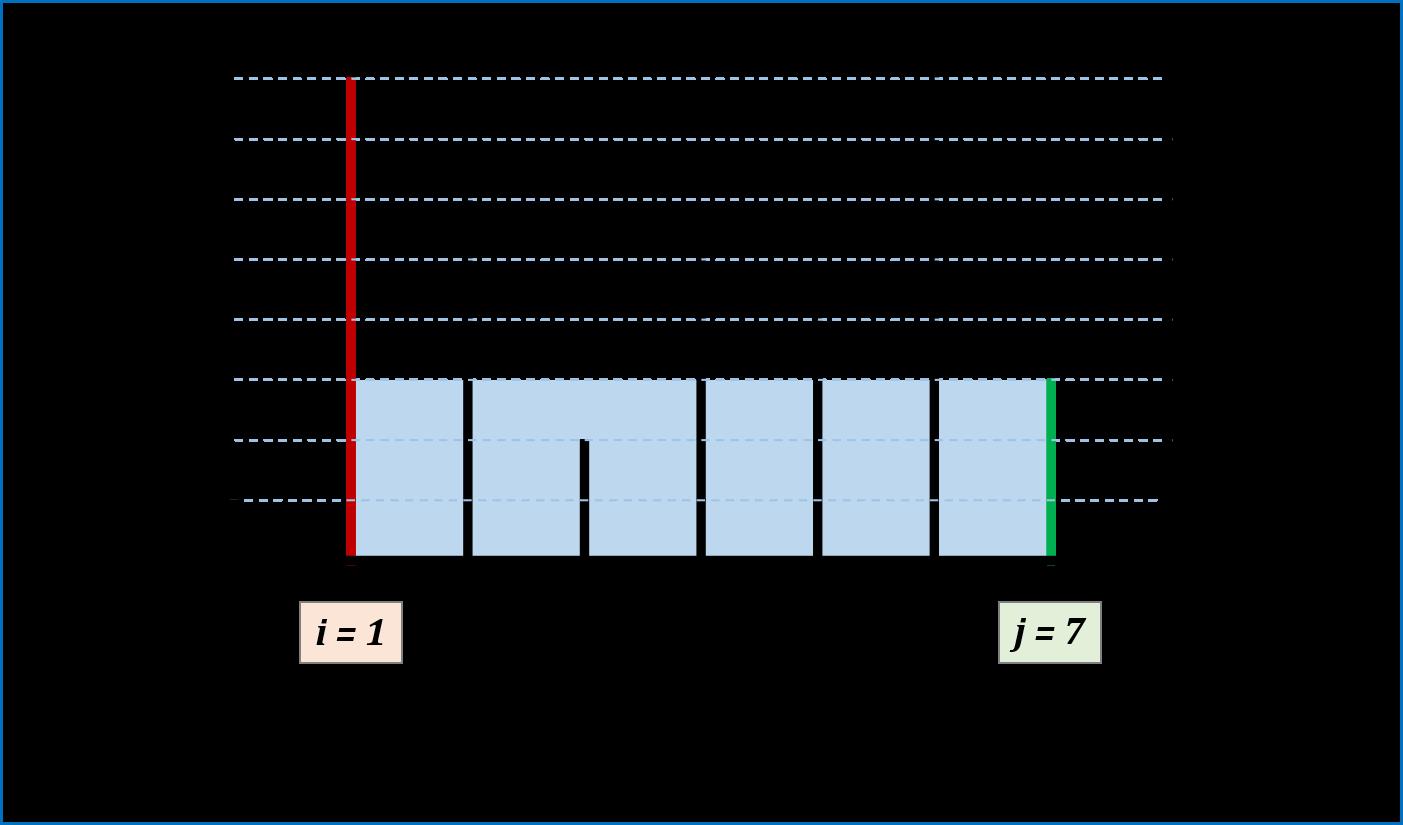
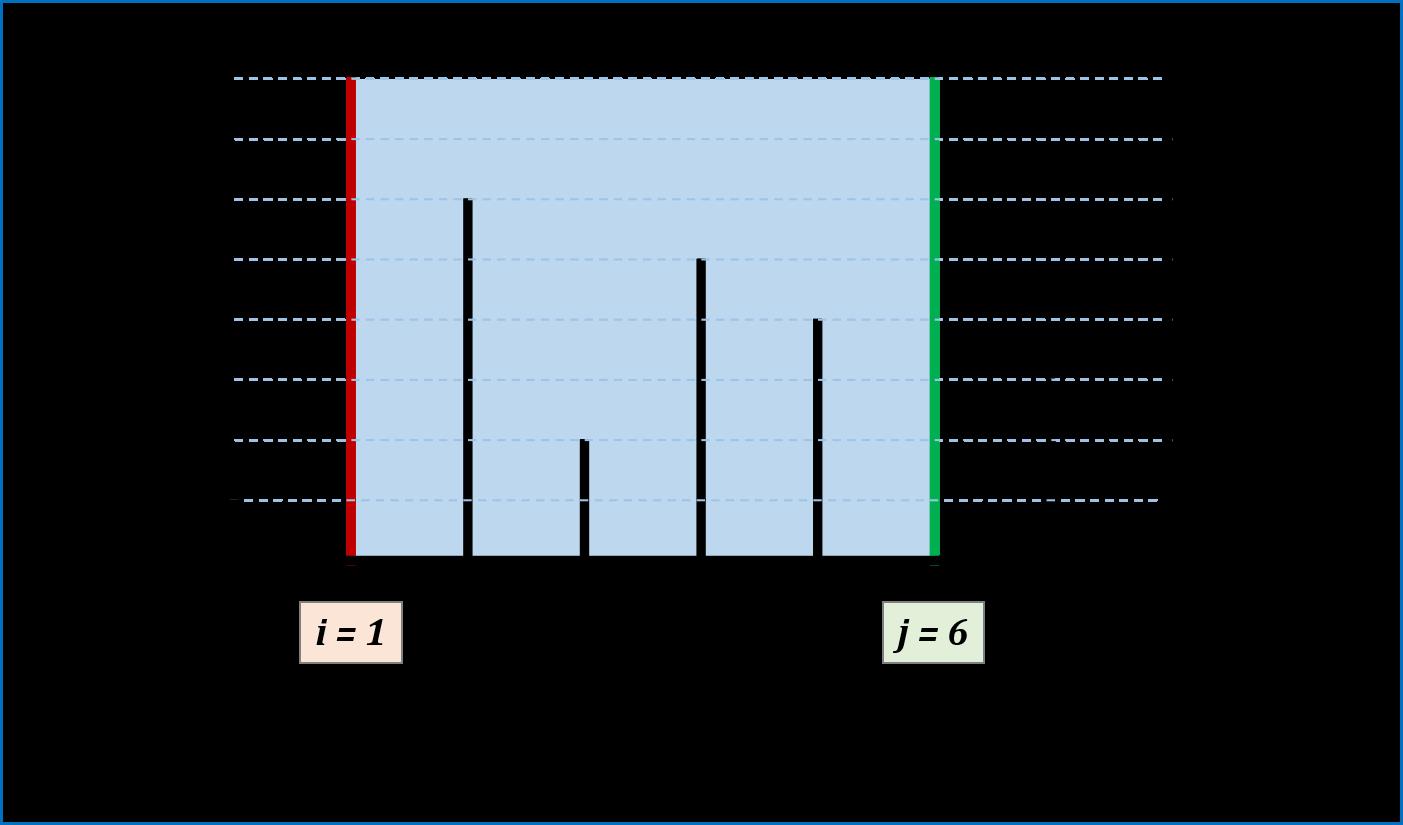
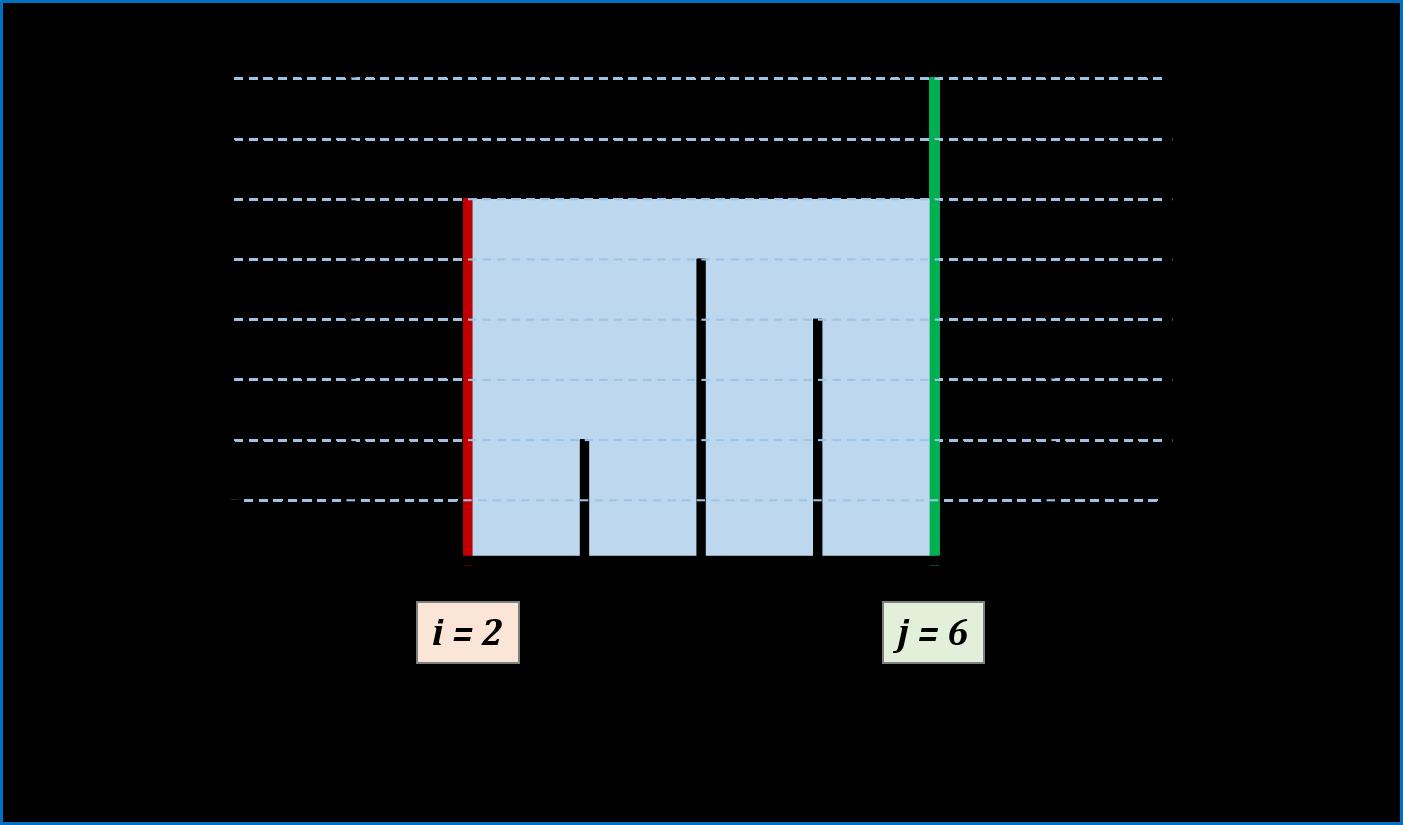
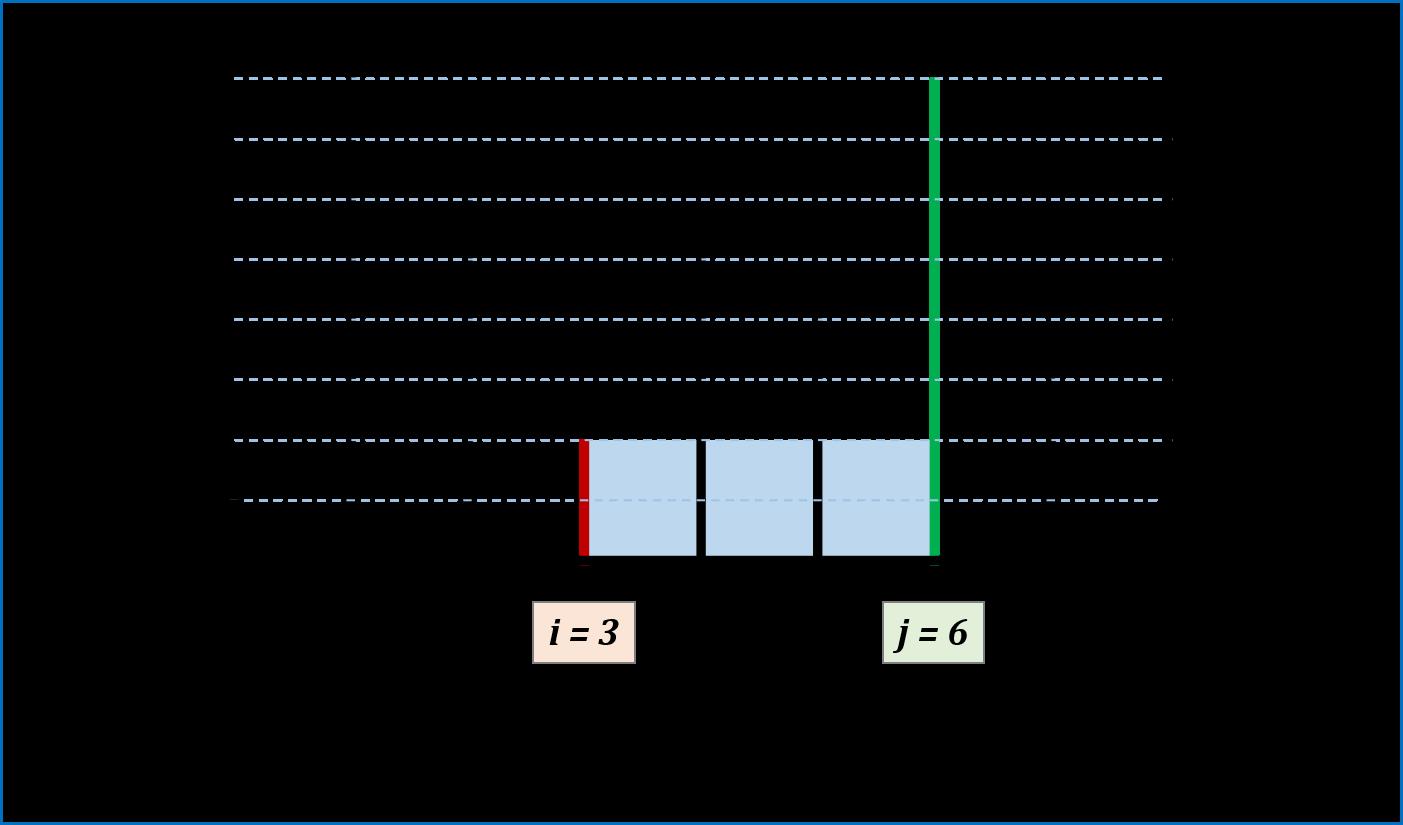
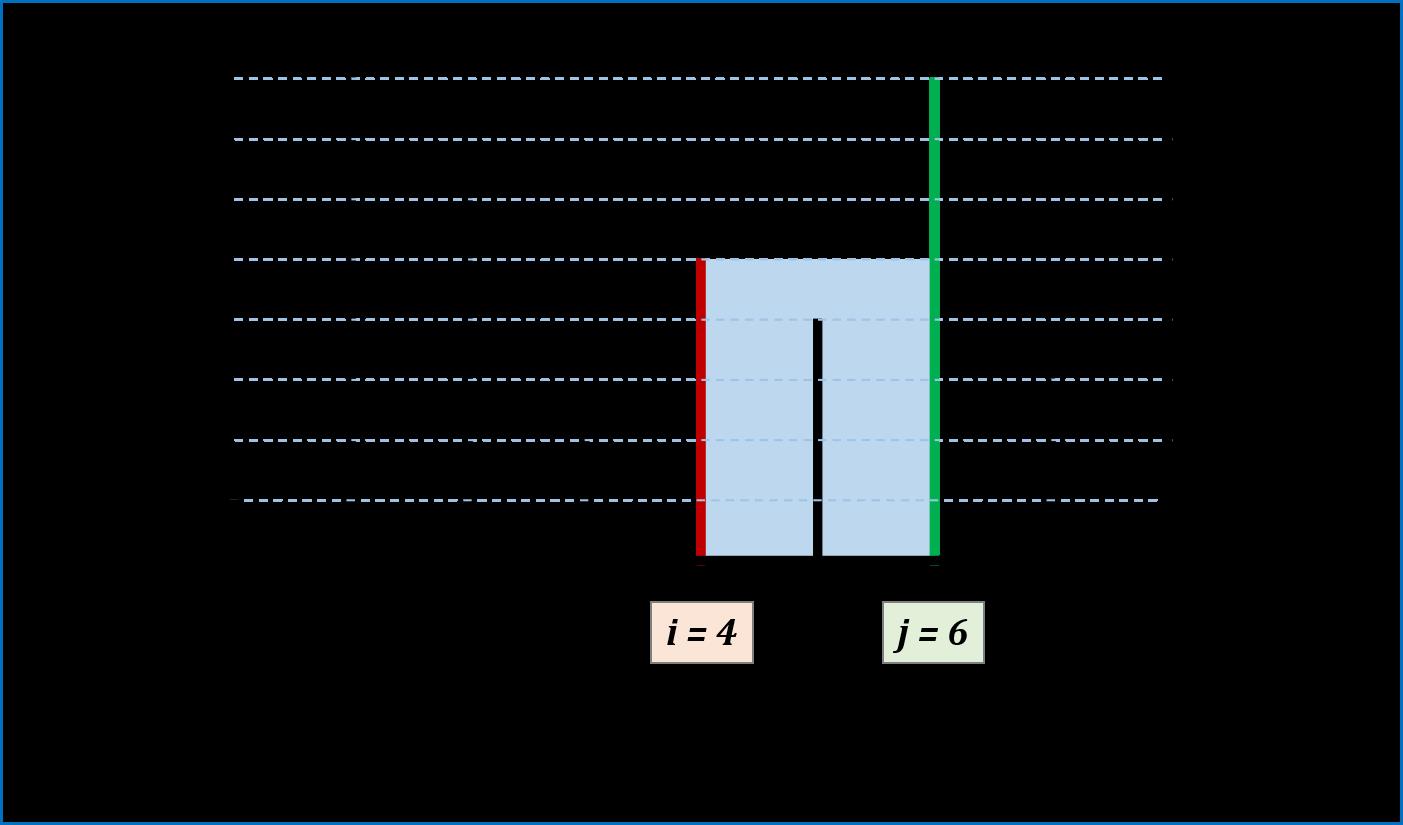
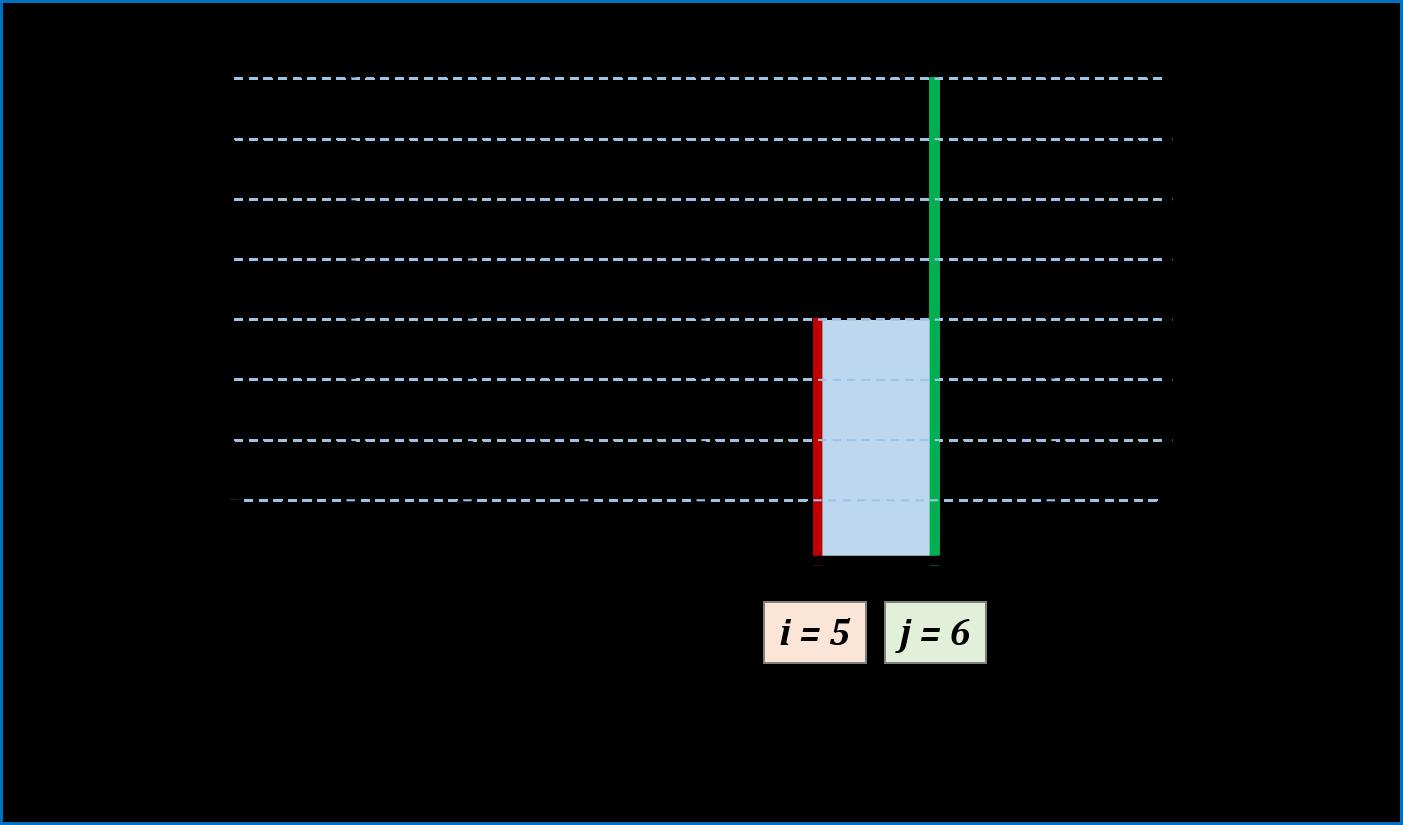
代码:

class Solution {
public:
	int maxArea(vector<int>& height)
	{
		int i = 0, j = height.size() - 1, res = 0;
		while (i < j)
			res = height[i] < height[j] ?
				max(res, (j - i) * height[i++]) :
				max(res, (j - i) * height[j--]);
		return res;
	}
};

\\