leetcode 46. 全排列----回溯篇5

Posted 2021-06-04 大忽悠爱忽悠

全排列题解集合

• 回溯法
• 总结

---

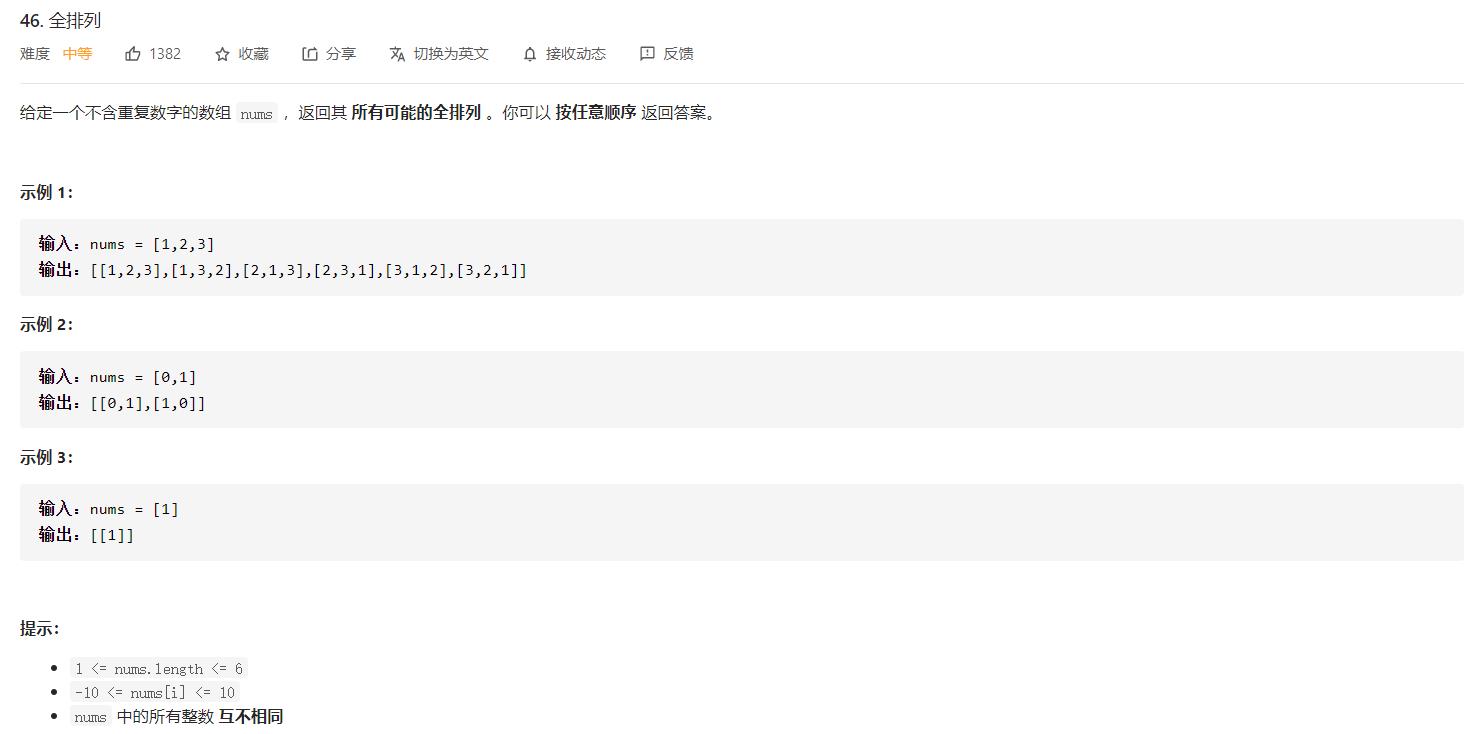
回溯法

把问题转化为对一个多叉树的遍历过程

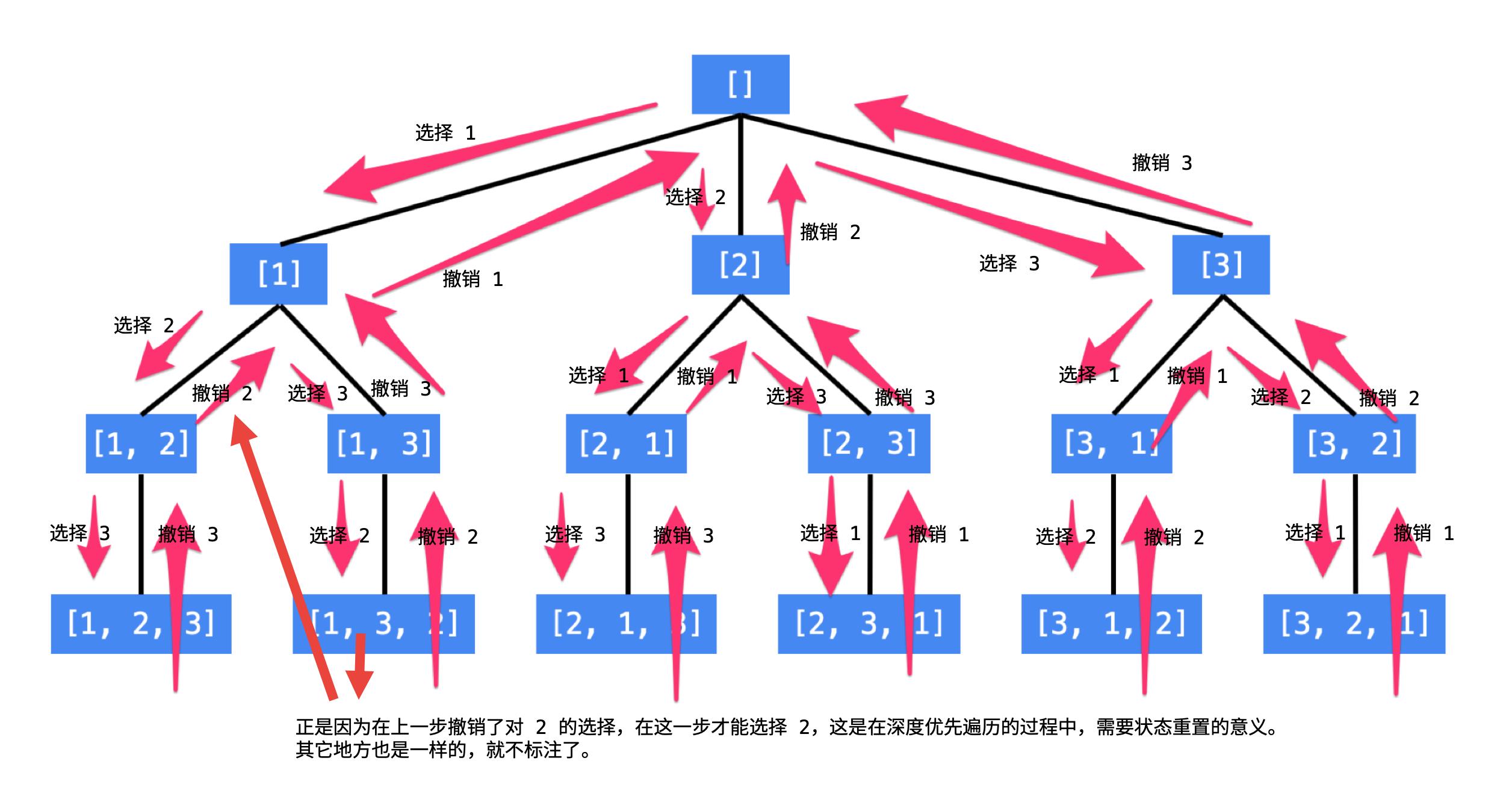
细节：

我们需要设置一个访问数组visited,防止一个数字被多次放入当前结果数组中。

举例: 数组【1，2，3】

一开始我们选择了数字1，然后进入二叉树第三层，此时我们需要从头开始选取，即从1开始选取，为什么呢？

当我们选择1后，可以直接从1后面的2和3开始选择，选2后只能选3，得到一个排列1，2，3

那么如果选了3后，应该往前取选择还没被选择的二，怎么往前去选择还没被选择的二呢？

当然是从头开始找，即从1开始到3之前结束，看看哪个数字还没在当前的结果数组中，怎么看哪个数字有没有被选择呢?

此时就需要一个标记数组，如果一个数字被选入当前的结果数组中，就设置标记为真，然后当我们要寻找一个没有被选进当前结果数组中的数字时，只需要看其对应的标记真假与否，如果为真，则跳过当前数字不选，继续寻找没有被选择的数字。

当一个数字从当前的结果数组中拿出，对应的也要将其的标志恢复为假

代码：

class Solution {
	vector<vector<int>> ret;
	vector<int> num;
	vector<bool> visited;
public:
	vector<vector<int>> permute(vector<int>& nums) 
	{
		if (nums.empty()) return ret;
		visited.resize(nums.size(), false);
		backTrace(nums);
		return ret;
	}
	void backTrace(vector<int>& nums)
	{
		if (num.size() == nums.size())
		{
			ret.push_back(num);
			return;
		}
		for (int i =0; i < nums.size(); i++)
		{
			if (visited[i]) continue;
			num.push_back(nums[i]);
			visited[i] = true;
			backTrace(nums);
			num.pop_back();
			visited[i] = false;
		}
	}
};

---

总结

注意与之前将的组合数的区别，例如:组合数种选择2，就不能再去考虑前面的1了，而对于排列而言，选择了2，也要去考虑前面的1

因此这里对于排列数而言，每一次循环都要从头看起，并且多了一个标志数组，用来记录当前元素，是否已经存在于结果数组中