洛谷-----P1028 [NOIP2001 普及组] 数的计算

Posted 2021-06-04 大忽悠爱忽悠

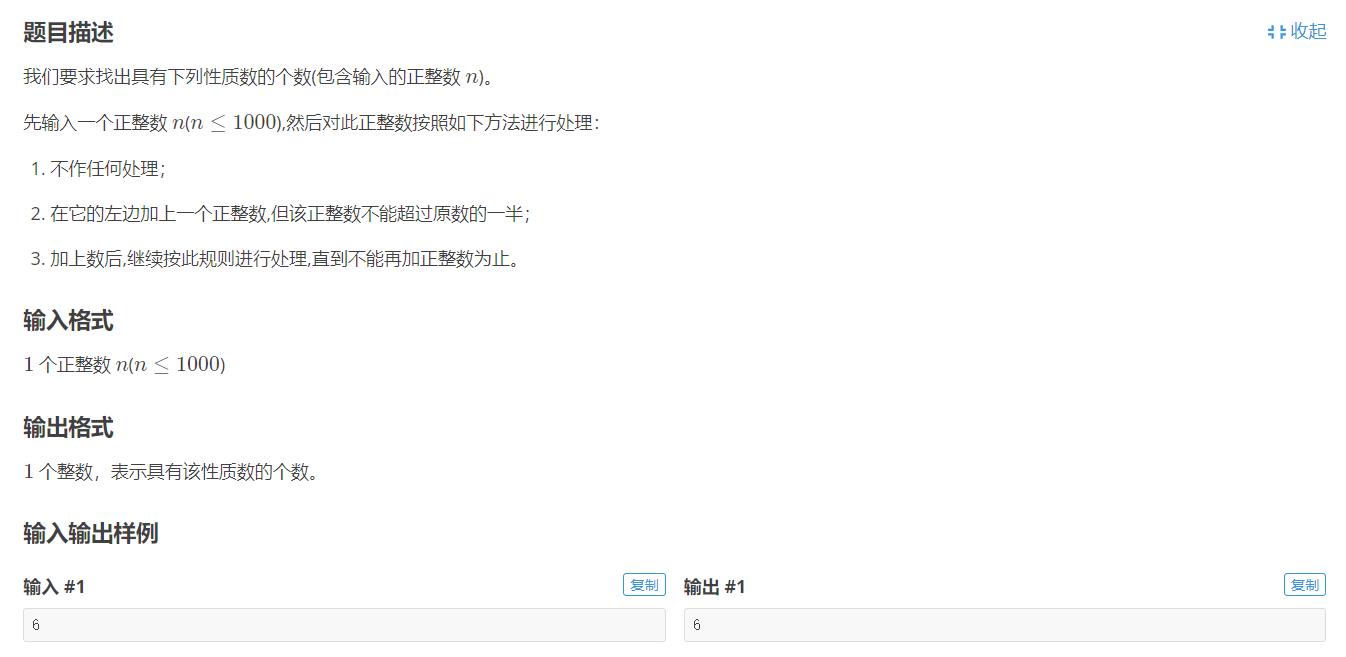
数的计算题解集合

• DFS
• 记忆化递归
• 动态规划---递推思想

---

DFS

把问题转化为对一颗多叉树的遍历，叶子的总数加上一个根节点的总数就是我们需要的结果

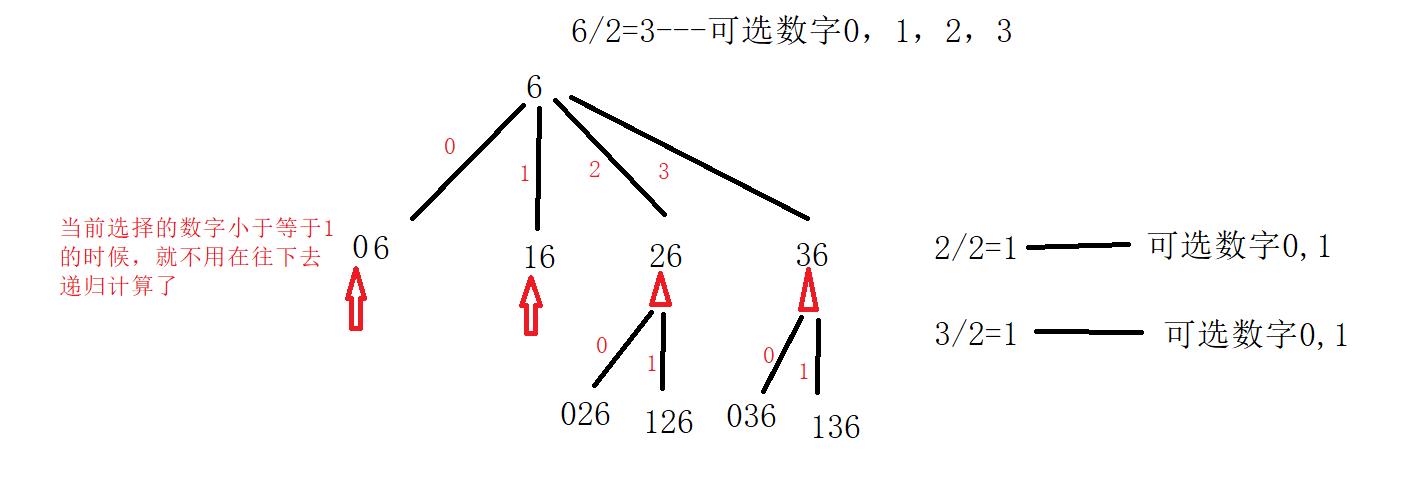
代码：

#include<iostream>
using namespace std;
class Solution {
public:
	int SumNum(int num)
	{
		int sum =0;
		//递归结束条件:
		if (num<= 1)
			return 1;
		for (int i = 0; i <=num / 2; i++)
		{
			sum += SumNum(i);
		}
		return sum;
	}
};

int main()
{
	Solution s;
	int n = 0;
	cin >> n;
	cout << s.SumNum(n) << endl;;
	return 0;
}

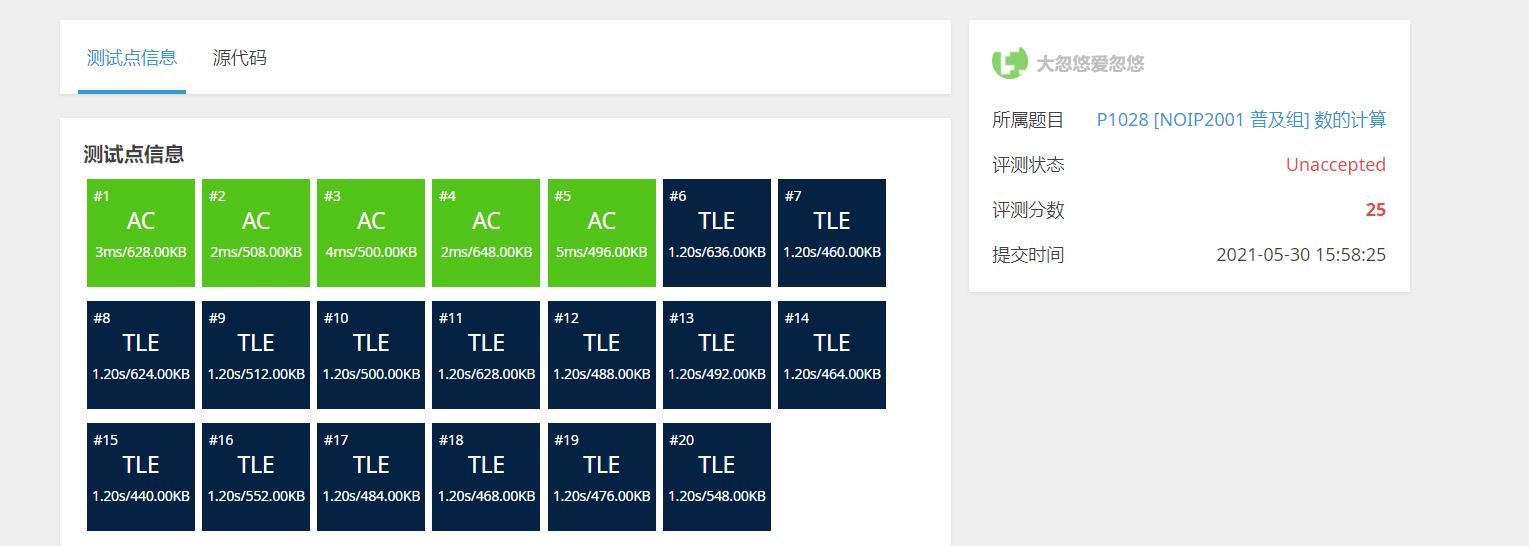
显然这里TLE,递归超时了

---

记忆化递归

首先思考，这里的重复计算出现在什么地方，这里我们才能对症下药,看下图:

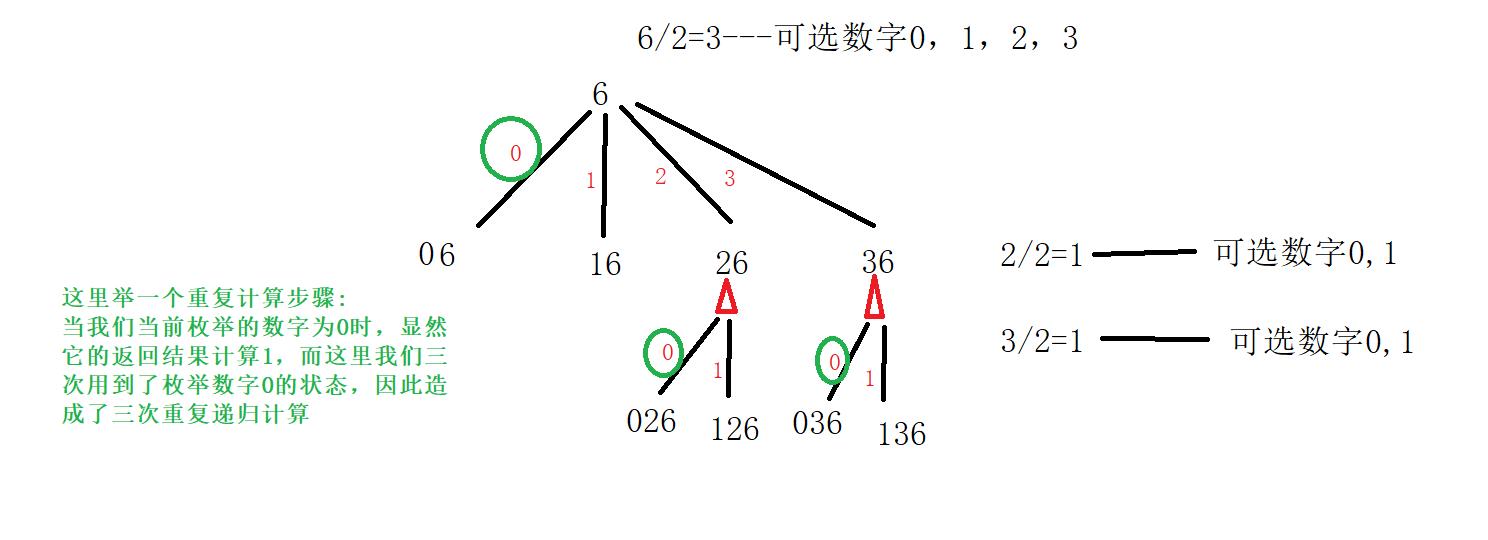
这里我们可以使用哈希表保存选择了当前数字后，得到的总数，等到下次用到的时候，直接返回即可

代码:

#include<iostream>
using namespace std;
#include<unordered_map>
class Solution {
	unordered_map<int, int> cache;
public:
	int SumNum(int num)
	{
		if (cache.find(num) != cache.end()) return cache[num];
		int sum =0;
		//递归结束条件:
		if (num<= 1)
			return 1;
		for (int i = 0; i <=num / 2; i++)
		{
			sum += SumNum(i);
		}
		return cache[num]=sum;
	}
};
int main()
{
	Solution s;
	int n = 0;
	cin >> n;
	cout << s.SumNum(n) << endl;;
	return 0;
}

---

动态规划—递推思想

先举一个例子:

以4为例子来进行说明

4后面可以跟上1,2组成14,24

14后面跟不了,24可以跟上1组成124

再加上4本身就可以得到4的种类

即 14,24,124,4

而我们只要算出1,2的种类就可以加起来得到4的种类

因此，我们得到:

f[1]=1
f[2]=2=f[1]+1
f[3]=2=f[1]+1
f[4]=4=f[1]+f[2]+1
f[5]=4=f[1]+f[2]+1

当然这里dp[1]也可以不作为最优子结构，把dp[0]作为最优子结构,即dp[1]=dp[0]+1=1;

dp[0]=0;

---

通过上面的举例也可以得到dp[i]的含义，即当前数字i可以分解得到的所有组合数

由此得到状态转移方程:dp[i]=dp[1]+dp[2]+…+dp[n]+1; (n<=i/2)

这里的dp数组初始化情况就是当前i=0时，dp[0]=0，显然数字0分解不了，因此组合数为0

代码:

#include<iostream>
using namespace std;
#include<vector>
class Solution {
public:
	int SumNum(int num)
	{
		vector<int> dp(num+1,0);
		dp[0]=0;
		for (int i = 1; i <=num; i++)
		{
			for (int j = 0;j <=i / 2; j++)
				dp[i] += dp[j];
			dp[i]++;
		}
		return dp[num];
	}
};
int main()
{
	Solution s;
	int n = 0;
	cin >> n;
	cout << s.SumNum(n) << endl;;
	return 0;
}