HDU 5673 Robot（默慈金数）

Posted 2021-06-04 jpphy0

链接

Robot - http://acm.hdu.edu.cn/showproblem.php?pid=5673

分析

• 从原点出发回到原点，且不会出现在原点左侧

• 从开始到任意时刻，向右步数不少于向左步数，且最终向右、向左步数相等；

• 若共$n$步，向右和向左各$k$步，则不动有$n-2k$步，因此， C n n − 2 k × C k ， k ∈ { 0 , 1 , 2 , … ， ⌊ n 2 ⌋ } C_n^{n-2k} \\times C_k，k\\in\\{0,1,2,…，\\lfloor\\frac{n}{2}\\rfloor\\} Cnn−2k​×Ck​，k∈{0,1,2,…，⌊2n​⌋}

• 这是一个 $\pm 1、0$ 模型，其中 $\pm 1$ 满足卡特兰模型

• 结论：$M_n=C_n^n\times C_0+C_n^{n-2}\times C_1+\dots +C_n^{n-2\times k}\times C_k+\dots +C_n^{n-2\times \lfloor \frac{n}{2}\rfloor }\times C_{\lfloor \frac{n}{2}\rfloor }$

• $C_k$为卡特兰数，$M_n$称为默慈金数（Motzkin Number）

  • 在一个圆上的n个点间画出彼此不相交的弦的全部方法的总数【允许某些或全部点不连线】

    • 4个点，9种连接方法
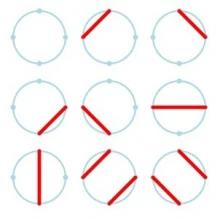
    • 5个点，21种连接方法

  • 在一个“网格”上，若限定“每步只能向右移动一格(可以向右上、右下横向向右)，并禁止移动到y=0以下的地方”，则以这种走法用n步从(0,0)移动至(n,0)的可能形成的路径的总数为n的默慈金数。
    

  • 最初的几个默慈金数如下（OEIS中的数列A001006）：1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019, 142547559, 400763223, 1129760415, 3192727797, 9043402501, 25669818476, 73007772802, 208023278209, 593742784829

  • 递推式：$$M_{n+1}=M_n+\sum _{i=0}^{n-1}{M}_i\times M_{n-1-i}=\frac{2n+3}{n+3}{M}_n+\frac{3n}{n+3}{M}_{n-1}$$

• 此外，本题取模运算涉及费马小定理求逆元

代码

默慈金数

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MXN 1000010
#define MOD 1000000007
ll mtz[MXN] =  {0, 1, 2}; // 默慈金数
ll inv(ll base, int power){ // 快速幂求逆元
	ll res = 1;
	while(power){
		if(power & 1) res = res*base%MOD;
		base = base*base%MOD;
		power >>= 1;
	}
	return res;
}
void init(){ // 打表
    for(int i = 2; i < MXN; i++){
        mtz[i+1] = (((2*i+3)*mtz[i] + 3*i*mtz[i-1])%MOD*inv(i+3, MOD-2))%MOD;
	}
}
int main(){
    int T, n;
	init();
	cin >> T;
    while(T--){
        cin >> n;
		cout << mtz[n] << endl;
    }
    return 0;
}