数据结构—— 线性结构：堆栈

Posted 大彤小忆

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构—— 线性结构：堆栈相关的知识，希望对你有一定的参考价值。

2. 堆栈

2.1 什么是堆栈

  计算机如何进行表达式求值?
  例： 算术表达式 5 + 6 / 2 − 3 ∗ 4 5+6/2-3* 4 5+6/2−3∗4，正确理解为 5 + 6 / 2 − 3 ∗ 4 = 5 + 3 − 3 ∗ 4 = 8 − 3 ∗ 4 = 8 − 12 = − 4 5+6/2-3* 4=5+3-3* 4=8-3* 4=8-12 =-4 5+6/2−3∗4=5+3−3∗4=8−3∗4=8−12=−4。
     • 由两类对象构成：
       ⋄ \\diamond ⋄ 运算数，如2、3、4
       ⋄ \\diamond ⋄ 运算符号，如+、-、*、/
     • 不同运算符号优先级不一样
  中缀表达式： 运算符号位于两个运算数之间。如， a ＋ b ∗ c − d / e a＋b*c- d/e a＋b∗c−d/e。
  后缀表达式： 运算符号位于两个运算数之后。如， a b c ∗ + d e / − a b c*+d e/- abc∗+de/−。
  例如 5 + 6 / 2 − 3 ∗ 4 5+6/2-3* 4 5+6/2−3∗4可以表达为 62 / 3 − 42 ∗ ＋ 62/3-42*＋ 62/3−42∗＋。
  后缀表达式求值策略：从左向右“扫描”，逐个处理运算数和运算符号。
    1. 遇到运算数怎么办?如何“记住”目前还未参与运算的数?
    2. 遇到运算符号怎么办?对应的运算数是什么?
  启示： 需要有种存储方法，能顺序存储运算数，并在需要时“倒序”输出！

  栈（stack）又名堆栈，它是一种运算受限的线性表，限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
  堆栈是一种数据项按序排列的数据结构，只能在一端(称为栈顶(top))对数据项进行插入和删除。

  堆栈(Stack）： 具有一定操作约束的线性表
     ⋄ \\diamond ⋄ 只在一端(栈顶, Top）做插入、删除
     ⋄ \\diamond ⋄ 插入数据：入栈(Push)
     ⋄ \\diamond ⋄ 删除数据：出栈（Pop)
     ⋄ \\diamond ⋄ 后入先出：Last In First Out (LIFO)

2.2 堆栈的抽象数据类型描述

  类型名称： 堆栈(Stack)
  数据对象集： 一个有0个或多个元素的有穷线性表
  操作集： 长度为MaxSize的堆栈S ∈ ∈ ∈ Stack，堆栈元素item ∈ ∈ ∈ ElementType

  1. Stack CreateStack( int MaxSize )：生成空堆栈，其最大长度为MaxSize；
  2. int IsFull( Stack S, int MaxSize )：判断堆栈s是否已满；
  3. void Push( Stack S, ElementType item )：将元素item压入堆栈；
  4. int IsEmpty ( Stack S )：判断堆栈s是否为空；
  5. ElementType Pop( Stack S )：删除并返回栈顶元素。

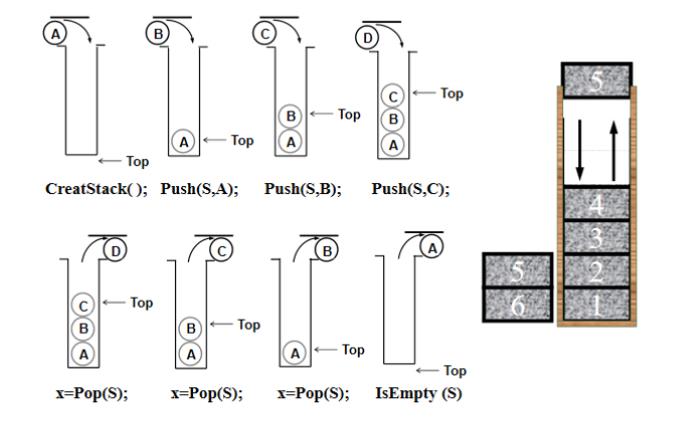
在这里插入图片描述
  Push和Pop可以穿插交替进行：
   (1) Push(S,A),Push(S,B),Push((S,C),Pop(S),Pop(S),Pop(S)
     堆栈输出是CBA
   (2) Push(S,A),Pop(S),Push(S,B),Push((S,C),Pop(S),Pop(S)
     堆栈输出是ACB

2.3 堆栈的顺序存储实现

  堆栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成。

  堆栈的顺序存储数据结构定义如下所示。

#define MaxSize<储存数据元素的最大个数>
typedef struct SNode *Stack;
struct SNode{
    ElementType Data[MaxSize];
    int Top;
}

  (1) 入栈

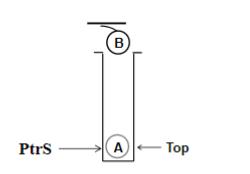
在这里插入图片描述

void Push(Stack Ptrs，ElementType item)
{
    if ( PtrS->Top == MaxSize-1 ) {
        cout << "堆栈满" << endl;
        return;
    }else {
        PtrS->Data[++(PtrS->Top)] = item;
        return;
}

  (2) 出栈

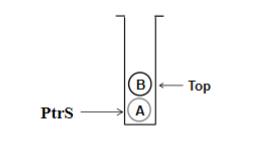
在这里插入图片描述

ElementType Pop(Stack Ptrs)
{
    if ( PtrS->Top ==-1 ){
        cout << "堆栈空" << endl;
        return ERROR;  //ERROR是ElementType的特殊值，标志错误
    else{
        return ( PtrS->Data[(PtrS->Top)--]);
    }
}

  堆栈的顺序存储实现实例的代码如下所示。

#include<iostream>
using namespace std;
#define MaxSize 100   // 堆栈元素的最大个数 
typedef int ElementType; // ElementType 暂时定义为 int 类型 
typedef struct SNode *Stack;
struct SNode {
	ElementType Data[MaxSize];   // 存储堆栈元素
	int Top;  // 记录栈顶元素下标 
};
Stack S;

Stack CreateStack();  // 初始化堆栈 
int IsFull(Stack S); // 判断堆栈是否已满 
int IsEmpty(Stack S);  // 判断堆栈是否为空 
void Push(Stack S, ElementType item);  // 入栈 
ElementType Pop(Stack S);  // 出栈

// 初始化堆栈 
Stack CreateStack() {
	S = (Stack)malloc(sizeof(struct SNode));
	S->Top = -1;
	return S;
}

// 是否已满 
int IsFull(Stack S) {
	return (S->Top == MaxSize - 1);
}

// 是否为空 
int IsEmpty(Stack S) {
	return (S->Top == -1);
}

// 入栈 
void Push(Stack S, ElementType item) {
	if (IsFull(S)) {   // Top 从 0 开始 
		cout << "堆栈满" << endl;
		return;
	}
	else {
		S->Top++;   // 栈顶元素加一 
		S->Data[S->Top] = item;   // 放进最上 
		return;
	}
}

// 出栈
ElementType Pop(Stack S) {
	if (IsEmpty(S)) {
		cout << "堆栈空" << endl;
		return NULL;
	}
	else {
		ElementType val = S->Data[S->Top];  //取出最上 
		S->Top--;  // 栈顶元素减一 
		return val;
	}
}
int main() {
	S = CreateStack();

	cout << "1入栈" << endl;
	Push(S, 5);

	cout << "2入栈" << endl;
	Push(S, 7);

	cout << "3入栈" << endl;
	Push(S, 66);

	cout << Pop(S) << "出栈" << endl;

	cout << Pop(S) << "出栈" << endl;

	system("pause");

	return 0;
}

  代码运行结果如下图所示。

在这里插入图片描述
  例： 请用一个数组实现两个堆栈，要求最大地利用数组空间，使数组只要有空间入栈操作就可以成功。
  分析： 一种比较聪明的方法是使这两个栈分别从数组的两头开始向中间生长，当两个栈的栈顶指针相遇时，表示两个栈都满了。

  实例的代码如下所示。

#include<iostream>
using namespace std;
#define MaxSize 100   // 堆栈元素的最大个数 
typedef int ElementType; // ElementType 暂时定义为 int 类型 
typedef struct DStack *Stack;
struct DStack {
	ElementType Data[MaxSize];   // 存储堆栈元素
	int Top1; //堆栈1的栈顶指针
	int Top2; //堆栈2的栈顶指针
};
Stack S;

Stack CreateStack();  // 初始化堆栈 
void Push(Stack S, ElementType item, int Tag);  // 入栈 
ElementType Pop(Stack S, int Tag);  // 出栈

// 初始化堆栈 
Stack CreateStack() 
{
	S = (Stack)malloc(sizeof(struct DStack));
	S->Top1 = -1;
	S->Top2 = MaxSize;
	return S;
}

// 入栈 
void Push(Stack S, ElementType item, int Tag)  //Tag作为区分两个堆栈的标志，取值为1和2
{
	if (S->Top2 - S->Top1 == 1) 
	{  
		cout << "堆栈满" << endl;
		return;
	}
	if (Tag == 1)   //对第一个堆栈进行操作
	{
		S->Data[++(S->Top1)] = item;
	}
	else {  //对第二个堆栈进行操作
		S->Data[--(S->Top2)] = item;
	}
}

// 出栈
ElementType Pop(Stack S, int Tag) 
{
	if (Tag == 1)  //对第一个堆栈进行操作
	{
		if (S->Top1 == -1)  //堆栈1为空
		{
			cout << "堆栈1空" << endl;
			return NULL;
		}
		else
			return S->Data[(S->Top1)--];
	}

	if (Tag == 2)  //对第二个堆栈进行操作
	{
		if (S->Top2 == MaxSize)  //堆栈2为空
		{
			cout << "堆栈2空" << endl;
			return NULL;
		}
		else
			return S->Data[(S->Top2)++];
	}
}
int main() {
	S = CreateStack();

	cout << "1入栈1" << endl;
	Push(S, 1, 1);

	cout << "2入栈1" << endl;
	Push(S, 2, 1);

	cout << "3入栈1" << endl;
	Push(S, 3, 1);

	cout << "1入栈2" << endl;
	Push(S, 1, 2);

	cout << "2入栈2" << endl;
	Push(S, 2, 2);

	cout << "3入栈2" << endl;
	Push(S, 3, 2);

	cout << Pop(S,1) << "出栈1" << endl;

	cout << Pop(S,2) << "出栈2" << endl;

	system("pause");

	return 0;
}

  代码运行结果如下图所示。

在这里插入图片描述

2.4 堆栈的链式存储实现

  堆栈的链式存储结构实际上就是一个单链表，叫做链栈。插入和删除操作只能在链栈的栈顶进行。栈顶指针Top应该在链表的哪一头?

  堆栈的链式存储数据结构定义如下所示。

typedef struct SNode *Stack;
struct SNode{
    ElementType Data;
    struct SNode *Next;
};

  (1) 堆栈初始化(建立空栈)
  (2) 判断堆栈s是否为空

在这里插入图片描述

Stack Createstack()
{  //构建一个堆栈的头结点,返回指针
    Stack S ;
    S=(Stack) malloc(sizeof (struct SNode));
    S->Next = NULL;
    return S;
}

int IsErmpty(Stack S)
{ //判断堆栈S是否为空,若为空函数返回整数1，否则返回0
    return ( S->Next == NULL);
}

  (1) 入栈

void Push(ElementType item, Stack S)
{ //将元素item压入堆栈S
    struct SNode *Tmpcell;
    Tmpcell=(struct SNode *) malloc(sizeof(struct SNode));
    Tmpcell->Element = item;
    Tmpcell->Next = S->Next;
    S->Next =TmpCell;
}

  (2) 出栈

ElementType Pop(Stack S)
{ //删除并返回堆栈S的栈顶元素
    struct SNode *Firstcell;
    ElementType TopElem ;
    if(IsEnmpty (S)){
        cout << "堆栈空" << endl;
        return NULL;
    }
    else {
        FirstCell = S->Next;
        S->Next = Firstcell->Next;
        TopElem = Firstcell ->Element;
        free(Firstcell);
        return TopElem;
    }
}

  堆栈的链式存储实现实例的代码如下所示。

#include<iostream>
using namespace std;
typedef int ElementType;
typedef struct SNode *Stack;
struct SNode {
	ElementType Data;
	Stack Next;
};
Stack S;

Stack CreateStack();  // 初始化链栈 
int IsEmpty(Stack S);  // 判断链栈是否为空 
void Push(Stack S, ElementType item);  // 入栈 
ElementType Pop(Stack S);  // 出栈


// 初始化 
Stack CreateStack() {
	S = (Stack)malloc(sizeof(struct SNode));
	S->Next = NULL;
	return S;
}

// 判断是否为空 
int IsEmpty(Stack S) {
	return (S->Next == NULL);
}

// 入栈
void Push(Stack S, ElementType item) {
	Stack tmp;
	tmp = (Stack)malloc(sizeof(struct SNode));
	tmp->Data = item;
	// 链栈栈顶元素是链表头结点，新入栈的链表在栈顶元素后面 
	tmp->Next = S->Next;
	S->Next = tmp;
}

// 出栈
ElementType Pop(Stack S) {
	Stack First;
	ElementType TopVal;
	if (IsEmpty(S)) {
		cout << "堆栈空" << endl;
		return NULL;
	}
	else {
		First = S->Next;   // 出栈第一个元素在栈顶元素后面 
		S->Next = First->Next;  //把第一个元素从链栈删除 
		TopVal = First->Data;   // 取出被删除结点的值 
		free(
以上是关于数据结构—— 线性结构：堆栈的主要内容，如果未能解决你的问题，请参考以下文章
 

 堆栈（线性表）


 数据结构 堆栈


 数据结构--------（堆栈 和 队列）


 数据结构 -- 栈队列树


 堆栈的应用——用JavaScript描述数据结构


 数据结构线性结构 —— 编程作业 04 ：Pop Sequence