递归算法

Posted 2021-06-03 大彤小忆

• 1. 递归算法概述
• 2. 利用递归算法计算阶乘
• 3. 利用递归算法实现二分查找
• 4. 利用递归算法进行排列组合

1. 递归算法概述

  程序调用自身的编程技巧称为递归（recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。
  递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

  递归，就是在运行的过程中调用自己。

  构成递归需具备的条件： 1. 子问题须与原始问题为同样的事，且更为简单；
              2. 不能无限制地调用本身，须有个出口，化简为非递归状况处理。

  递归算法一般用于解决三类问题：1. 数据的定义是按递归定义的。(Fibonacci函数）
                 2. 问题解法按递归算法实现。这类问题虽则本身没有明显的递归结构，但用递归求解比迭代求解更简单，如Hanoi问题。
                 3. 数据的结构形式是按递归定义的。

  递归的缺点：递归算法解题相对常用的算法如普通循环等，运行效率较低。因此，应该尽量避免使用递归，除非没有更好的算法或者某种特定情况，递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。

  迭代（iteration）是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

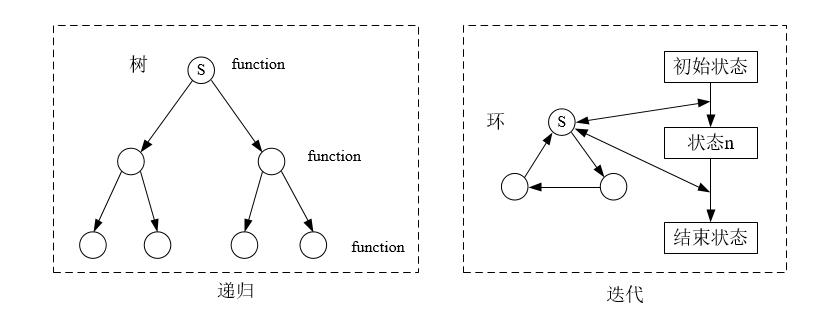
  递归与迭代的区别：

• 递归常被用来描述以自相似方法重复事物的过程，在数学和计算机科学中，指的是在函数定义中使用函数自身的方法。（A调用A）
  迭代是重复反馈过程的活动，每一次迭代的结果会作为下一次迭代的初始值。（A重复调用B）
• 递归是一个树结构，从字面可以其理解为重复“递推”和“回归”的过程，当“递推”到达底部时就会开始“回归”，其过程相当于树的深度优先遍历。
  迭代是一个环结构，从初始状态开始，每次迭代都遍历这个环，并更新状态，多次迭代直到到达结束状态。
• 理论上递归和迭代的时间复杂度是一样的，但实际应用中（函数调用和函数调用堆栈的开销）递归比迭代效率要低。

2. 利用递归算法计算阶乘

  例如： 计算5的阶乘。

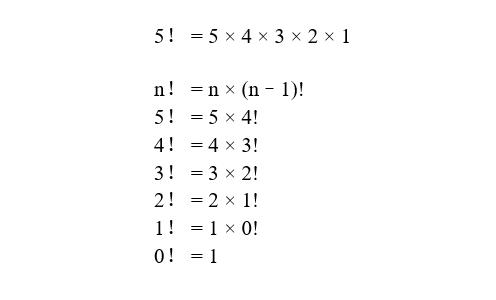
  实现代码如下所示。

#include<iostream>
using namespace std;

// n! = n x (n-1)!
int factorial_Recursion(int n)  //利用递归
{
	if (n == 0)
	{
		return 1;
	}
	else
	{
		return n * factorial_Recursion(n - 1);
	}
}

long factorial_Iteration(int n)  //利用迭代（即循环）
{
	long result = 1;  //用long类型来防止阶乘的值超出int型的范围
	for (int i = n; i > 0; i--)
	{
		result = result * i;
	}
	return result;
}

int main()
{
	int n = 5;

	cout << "递归：" << n << "! = " << factorial_Recursion(n) << endl;
	cout << "迭代：" << n << "! = " << factorial_Iteration(n) << endl;

	system("pause");

	return 0;
}

递归：5! = 120
迭代：5! = 120

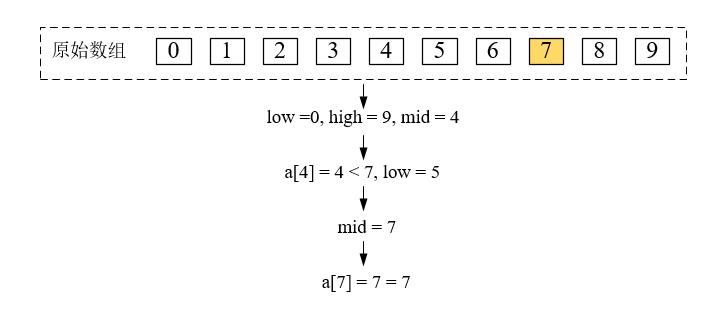
3. 利用递归算法实现二分查找

  例如： 使用二分查找算法在数组 { 0,1,2,3,4,5,6,7,8,9 }中查找元素7。

  实现代码如下所示。

#include<iostream>
using namespace std;

// 二分查找
int BinarySearch_Recursion(int *a, const int low, const int high, const int x)  //利用递归
{
	if (low <= high)
	{
		int mid = low + (high - low);
		if (x == a[mid])
		{
			return mid;
		}
		else if (x < a[mid])
		{
			return BinarySearch_Recursion(a, low, mid - 1, x);
		}
		else if (x > a[mid])
		{
			return BinarySearch_Recursion(a, mid + 1, high, x);
		}
	}
}

int BinarySearch_Iteration(int *a, const int n, const int x)  //利用迭代（即循环）
{
	int low = 0;
	int high = n - 1;
	int mid;

	while (low <= high)
	{
		mid = low + (high - low);
		if (x == a[mid])
		{
			return mid;
		}
		else if (x < a[mid])
		{
			high = mid - 1;
		}
		else if (x > a[mid])
		{
			low = mid + 1;
		}
	}
	return -1;
}

int main()
{
	int a[] = { 0,1,2,3,4,5,6,7,8,9 };

	int num = 7;

	int result1 = BinarySearch_Recursion(a, 0, 9, num);
	if (result1 == -1)
	{
		cout << "递归：未找到！" << endl;
	}
	else
	{
		cout << "递归：在a[" << result1 << "]里找到" << num << endl;
	}

	int result2 = BinarySearch_Iteration(a, 9, num);
	if (result2 == -1)
	{
		cout << "迭代：未找到！" << endl;
	}
	else
	{
		cout << "迭代：在a[" << result2 << "]里找到" << num << endl;
	}

	system("pause");

	return 0;
}

递归：在a[7]里找到7
迭代：在a[7]里找到7

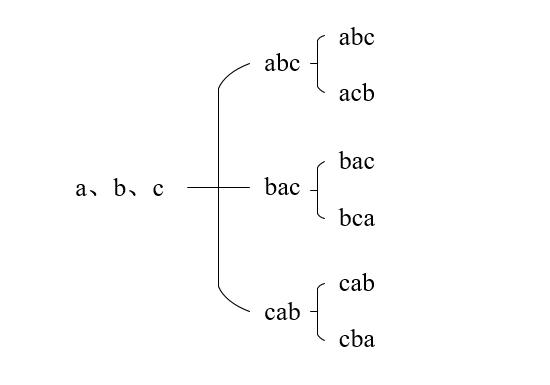
4. 利用递归算法进行排列组合

  例如： 对字母a、b、c进行排列组合。

  实现代码如下所示。

#include<iostream>
using namespace std;

// 排列组合（Permutations）
void Permutations(char *p, const int k, const int m)  //利用递归
{
	if (k == m)
	{
		for (int i = 0; i <= m; i++)
		{
			cout << p[i];
		}
		cout << endl;
	}
	else
	{
		for (int i = k; i <= m; i++)
		{
			swap(p[k], p[i]);
			Permutations(p, k + 1, m);
			swap(p[k], p[i]);
		}
	}
}

int main()
{
	char s[] = "abc";
	Permutations(s, 0, 2);  // 0指a；2指c

	system("pause");

	return 0;
}

abc
acb
bac
bca
cba
cab

  递归过程如下图所示。

  查看代码运行的中间过程，实现代码如下所示。

#include<iostream>
using namespace std;

int num1 = 0;  //统计Permutations()函数调用次数
int num2 = 0;  //统计递归返回次数

// 排列组合（Permutations）

void show(char *p, int m)
{
	for (int i = 0; i <= m; i++)
	{
		cout << p[i];
	}
	cout << endl;
}

void Permutations(char *p, const int k, const int m)  //利用递归
{
	cout << "Permutations()函数调用次数：" << ++num1 << endl;

	if (k == m)
	{
		for (int i = 0; i <= m; i++)
		{
			cout << p[i];
		}
		cout << endl;
	}
	else
	{
		for (int i = k; i <= m; i++)
		{
			cout << "递归前，交换前：";
			show(p, m);

			swap(p[k], p[i]);
			cout << "递归前，交换后：";
			show(p, m);

			Permutations(p, k + 1, m);
			cout << "递归返回次数：" << ++num2 << endl;
			cout << "递归后，交换前：";
			show(p, m);

			swap(p[k], p[i]);
			cout << "递归后，交换后：";
			show(p, m);
		}
	}
}

int main()
{
	char s[] = "abc";
	Permutations(s, 0, 2);  // 0指a；2指c

	system("pause");

	return 0;
}

  运行结果如下图所示。

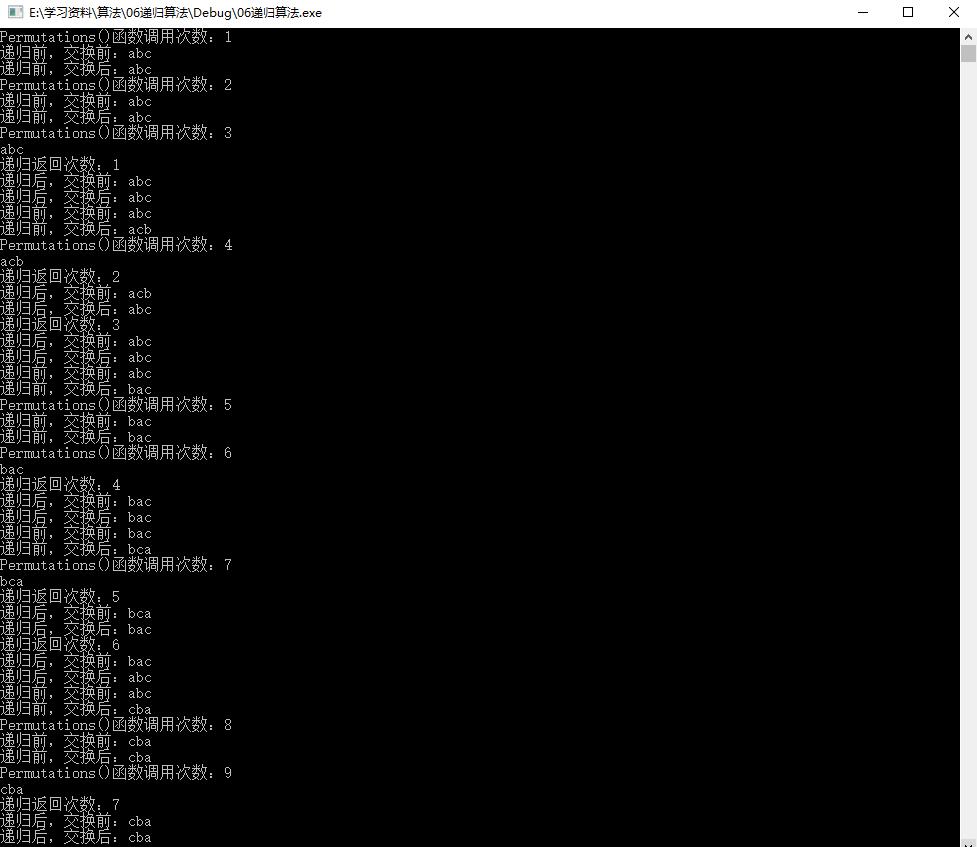
  代码运行的中间过程如下图所示，共调用Permutations()函数10次。