数据结构—— 树：树与树的表示

Posted 2021-06-03 大彤小忆

• 1. 树与树的表示
• • 1.1 什么是树
  • 1.2 查找
  • • 1.2.1 静态查找
  • 1.3 树的定义
  • 1.4 树的一些基本术语
  • 1.5 树的表示

1. 树与树的表示

1.1 什么是树

  树是一种数据结构，它是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

  树具有以下的特点：
  （1）每个结点有零个或多个子结点；
  （2）没有父结点的结点称为根结点；
  （3）每一个非根结点有且只有一个父结点；
  （4）除了根结点外，每个子结点可以分为多个不相交的子树。

  客观世界中许多事物存在层次关系：
   $\diamond$ 人类社会家谱
   $\diamond$ 社会组织结构
   $\diamond$ 图书信息管理

  分层次组织在管理上具有更高的效率！

1.2 查找

  数据管理的基本操作之一：查找。如何实现有效率的查找?

  查找(Searching)： 根据某个给定关键字K，从集合R中找出关键字与K相同的记录。
           $\diamond$ 静态查找： 集合中记录是固定的
                  没有插入和删除操作，只有查找
           $\diamond$ 动态查找： 集合中记录是动态变化的
                  除查找，还可能发生插入和删除

1.2.1 静态查找

• 方法1：顺序查找（详细内容参见顺序查找算法）

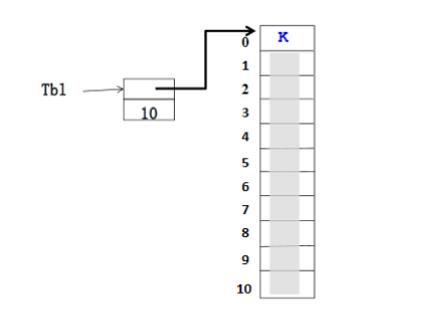
  顺序查找算法的代码如下所示。

int SequentialSearch(StaticTable *Tb1, ElementType K)
{  //在表bl[1]～Tbl[n]中查找关键字为K的数据元素
    int i;
    Tb1->Element[0]= K;  //建立哨兵
    for(i = Tb1->Length; Tb1->Element[i]!=K; i--)
        return i;  //查找成功返回所在单元下标，不成功返回0
}

  顺序查找算法的时间复杂度为$O(n)$。

• 方法2：二分查找（详细内容参见二分查找算法）
       假设$n$个数据元素的关键字满足有序（比如：小到大)，即$k_1<k_2<\dots <k_n$，并且是连续存放（数组)，那么可以进行二分查找。

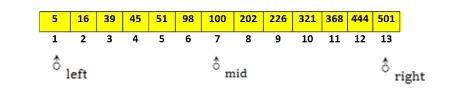
  例： 假设有13个数据元素，按关键字由小到大顺序存放。

  $\star$ 查找成功的情况： 二分查找关健字为444的数据元素过程如下所示。

    1. left= 1, right= 13；mid = (1+13)/2=7：100<444；

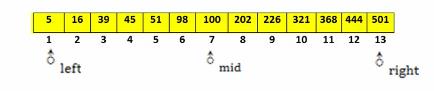
    2. left = mid+1=8，right = 13；mid = (8+13)/2=10：321<444；

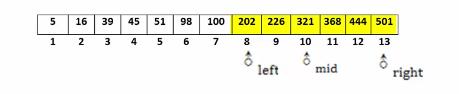
    3. left = mid+1=11，right = 13；mid = (11+13)/2=12：444=333，查找结束。

  $\star$ 查找失败的情况： 二分查找关健字为43的数据元素过程如下所示。
    1. left = 1，right = 13；mid = (1+13)/2 =7：100 > 43；

    2. left = 1，right = mid-1= 6；mid =(1+6)/2=3：39<43；

    3. left = mid+1=4，right = 6；mid =(4+6)/2 =5：51 > 43；
    4. left = 4，right = mid-1= 4；mid =(4+4)/2=4：45>43；
    5. left = 4，right = mid-1= 3；left > right ?查找失败，结束。

  二分查找算法的代码如下所示。

int BinarySearch(Static Table * Tbl, Element Type K)
{  //在表Tbl中查找关键字为K的数据元素
    int left, right, mid, NoFound=-1;
    left = 1;  //初始左边界
    right = Tbl->Length;  //初始右边界
    while (left <= right)
    {
        mid = (left+right)/2;  //计算中间元素坐标
        if(K < Tbl->Element[mid])
            right = mid-1;  //调整右边界
        else if(K > Tbl->Element[mid]) 
            left = mid+1;  //调整左边界
        else 
            return mid;  //查找成功，返回数据元素的下标
    }
    return NotFound;  //查找不成功，返回-1
}

  二分查找算法具有对数的时间复杂度$O(Iogn)$。

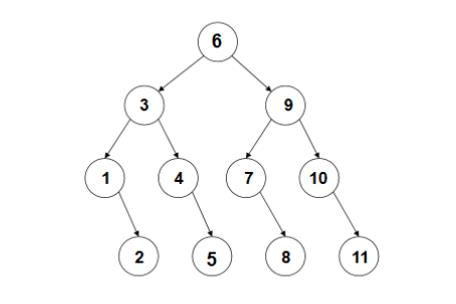
  11个元素的二分查找判定树：
   $\diamond$ 判定树上每个结点需要的查找次数刚好为该结点所在的层数；
   $\diamond$ 查找成功时查找次数不会超过判定树的深度；
   $\diamond$ n个结点的判定树的深度为$[lo{g}_{2}n]+1$；
   $\diamond$ 平均成功查找次数：ASL=(4 * 4 + 4 * 3 + 2 * 2 + 1) / 11 = 3。

1.3 树的定义

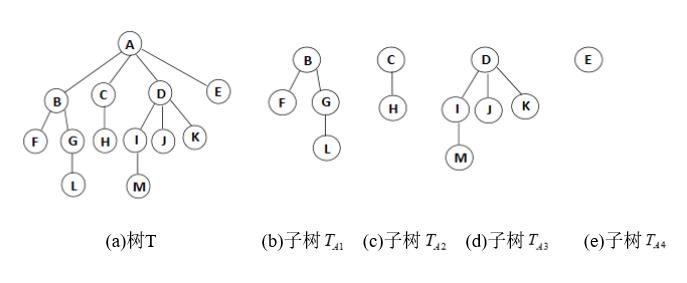
  树(Tree) ： n (n≥0)个结点构成的有限集合。
        当n=0时，称为空树；
        对于任一棵非空树(n>0)，它具备以下性质：
          $\diamond$ 树中有一个称为“根（Root)”的特殊结点，用r表示；
          $\diamond$ 其余结点可分为m(m>0)个互不相交的有限集$T_1,T_2,...,T_m$，其中每个集合本身又是一棵树，称为原来树的“子树(subTree)”。

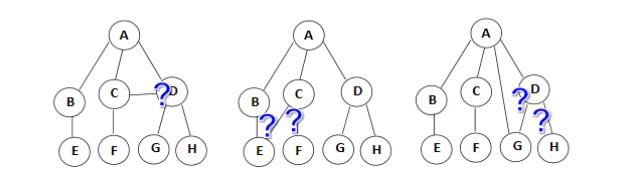
  树与非树？
    $\diamond$ 子树是不相交的；
    $\diamond$ 除了根结点外，每个结点有且仅有一个父结点；
    $\diamond$ 一棵N个结点的树有N-1条边。

  下图是一些非树的例子。

1.4 树的一些基本术语

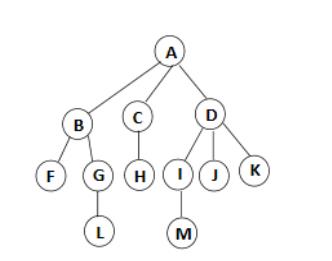
1. 结点的度（Degree)： 结点的子树个数。
2. 树的度： 树的所有结点中最大的度数。
3. 叶结点（Leaf)： 度为0的结点。
4. 父结点（Parent) ： 有子树的结点是其子树的根结点的父结点。
5. 子结点（Child）： 若A结点是B结点的父结点，则称B结点是A结点的子结点；
              子结点也称孩子结点。
6. 兄弟结点（Sibling）： 具有同一父结点的各结点彼此是兄弟结点。
7. 路径和路径长度： 从结点$n_1$到$n_k$的路径为一个结点序列$n_1,n_2,..,n_k$，$n_i$是$n_{i+1}$的父结点；
            路径所包含边的个数为路径的长度。
8. 祖先结点(Ancestor)： 沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。
9. 子孙结点(Descendant)： 某一结点的子树中的所有结点是这个结点的子孙。
10. 结点的层次(Level)： 规定根结点在1层，其它任一结点的层数是其父结点的层数加1。
11. 树的深度（Depth) ： 树中所有结点中的最大层次是这棵树的深度。

1.5 树的表示

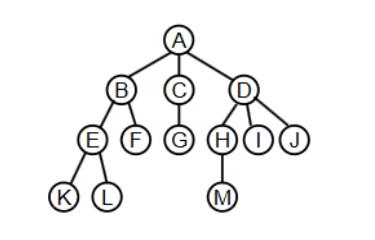
  树的表示用链表实现如下图所示。
   $\diamond$ 好处： 树中所有结点的结构是统一的，处理起来比较方便；
   $\diamond$ 问题： 如果树有n个结点，则树就有3n个指针域，但边只有n-1条，即只有n-1个指针是非零的，那么就有2n+1个指针域是空的，造成大的空间上的浪费。

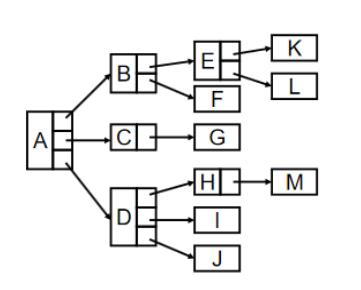
  比较好的一种表示方法是儿子-兄弟表示法，如下图所示。

  一个指针指向第一个儿子FirstChild，另一个指针指向下一个兄弟NextSibling。
   $\diamond$ 好处： 树中所有结点的结构是统一的，都为两个指针域；
        如果树有n个结点，则树就有2n个指针域，树有n-1条边，所有就有n-1个指针域是空的，造成空间上的浪费也不大。

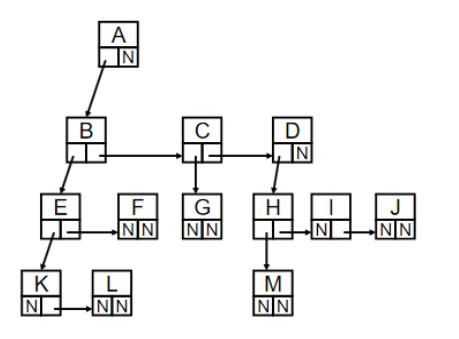
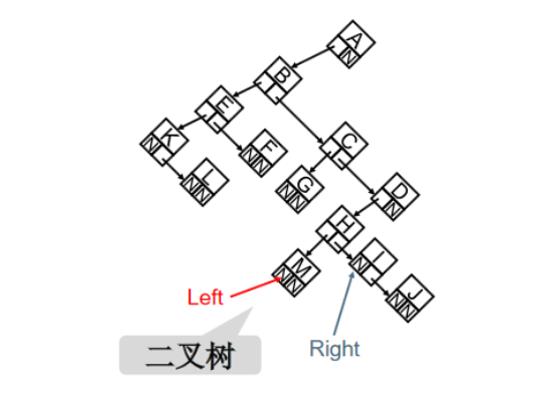
  将上述所示的儿子-兄弟表示法表示的树，顺时针旋转$45^{\circ }$，就是二叉树，即度为2的一种树。

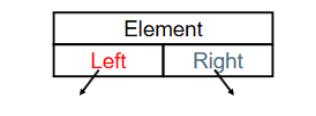
  一个指针指向左子树子Left，另一个指针指向右子树Right。