数据结构树 —— 编程作业 06 ：Root of AVL Tree

Posted 2021-06-03 大彤小忆

  题目描述： AVL树是一种自平衡二叉搜索树。在AVL树中，任意节点的两个子树的高度最多相差1。如果在任何时候它们的差超过1，则会进行重新平衡以恢复此属性。旋转规则如下图所示。

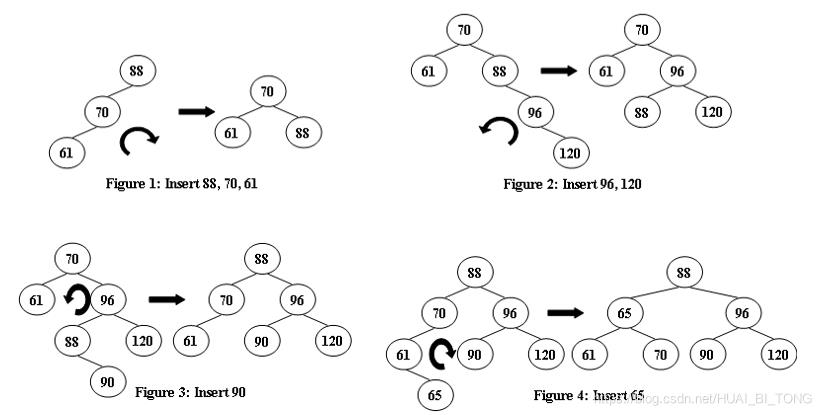
  现给定一个插入序列，需要得到的AVL树的根。

  输入格式： 每个输入文件包含一个测试用例。
        对于每种情况，第一行包含一个正整数N($⩽$ 20)，为要插入的元素的总数。
        然后在下一行给出N个不同的整数元素。
        一行中的所有数字都用空格隔开。

  输出格式： 对于每个测试用例，将生成的AVL树的根打印在一行中。

  输入样例1（对应图2）：

5
88 70 61 96 120

  输出样例1：

70

  输入样例2（对应图4）：

7
88 70 61 96 120 90 65

  输出样例2：

88

  代码实现：

#include<iostream>
using namespace std;
typedef struct AVLNode *AVLTree;
struct AVLNode {
	int data;     // 存值 
	AVLTree left;  // 左子树 
	AVLTree right;  // 右子树 
	int height;  // 树高 
};

// 返回最大值 
int Max(int a, int b)
{
	return a > b ? a : b;
}

// 返回树高，空树返回-1 
int getHeight(AVLTree A)
{
	return A == NULL ? -1 : A->height;
}

// LL旋转
// 把B的右子树腾出来挂上A的左子树，再将A挂在B的右子树上，返回B作为当前子树的根
AVLTree LLRotation(AVLTree A)
{
	// 此时根节点是A 
	AVLTree B = A->left;  // B为A的左子树  
	A->left = B->right;  // B的右子树挂在A的左子树上 
	B->right = A;   // A挂在B的右子树上 
	A->height = Max(getHeight(A->left), getHeight(A->right)) + 1;
	B->height = Max(getHeight(B->left), A->height) + 1;
	return B;  // 此时B为根结点 
}

// RR旋转
// 把B的左子树腾出来挂到A的右子树上，再将A挂在B的左子树上，返回B作为当前子树的根
AVLTree RRRotation(AVLTree A)
{
	// 此时根节点是A 
	AVLTree B = A->right;  // B为A的右子树
	A->right = B->left;   // B的左子树挂在A的右子树上
	B->left = A;   // A挂在B的左子树上
	A->height = Max(getHeight(A->left), getHeight(A->right)) + 1;
	B->height = Max(getHeight(B->left), A->height) + 1;
	return B;  // 此时B为根结点 
}

// LR旋转 
// 先将B(A->left)作为根结点进行RR旋转，再将A作为根结点进行LL旋转
AVLTree LRRotation(AVLTree A)
{
	// 先RR旋转
	A->left = RRRotation(A->left);
	// 再LL旋转 
	return LLRotation(A);
}

// RL旋转
// 先将B(A->right)作为根结点进行LL旋转，再将A作为根结点进行RR旋转
AVLTree RLRotation(AVLTree A)
{
	// 先 LL 单旋
	A->right = LLRotation(A->right);
	// 再 RR 单旋 
	return RRRotation(A);
}

AVLTree Insert(AVLTree T, int x)
{
	if (!T)  // 如果该结点为空，初始化结点
	{
		T = (AVLTree)malloc(sizeof(struct AVLNode));
		T->data = x;
		T->left = NULL;
		T->right = NULL;
		T->height = 0;
	}
	else   // 否则不为空
	{
		if (x < T->data)  // 左子树
		{
			T->left = Insert(T->left, x);
			if (getHeight(T->left) - getHeight(T->right) == 2)   // 如果左子树和右子树高度差为 2 
			{
				if (x < T->left->data)  // LL旋转 
					T = LLRotation(T);
				else if (x > T->left->data)  // LR旋转
					T = LRRotation(T);
			}
		}
		else if (x > T->data)   // 右子树
		{
			T->right = Insert(T->right, x);
			if (getHeight(T->right) - getHeight(T->left) == 2)
			{
				if (x < T->right->data)  // RL旋转 
					T = RLRotation(T);
				else if (x > T->right->data)  // RR旋转
					T = RRRotation(T);
			}
		}
	}
	//更新树高 
	T->height = Max(getHeight(T->left), getHeight(T->right)) + 1;
	return T;
}

int main()
{
	AVLTree T = NULL;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int tmp;
		cin >> tmp;
		T = Insert(T, tmp);
	}
	cout << T->data << endl;
	system("pause");
	return 0;
}

  测试：

• 测试1： 输入样例1的测试效果如下图所示。

• 测试2：输入样例2的测试效果如下图所示。