数据结构—— 树：平衡二叉树

Posted 大彤小忆

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构—— 树：平衡二叉树相关的知识，希望对你有一定的参考价值。

6. 平衡二叉树

6.1 什么是平衡二叉树

  平衡二叉树一般指平衡树。平衡树(Balance Tree，BT) 指的是，任意节点的子树的高度差都小于等于1。常见的符合平衡树的有B树（多路平衡搜索树）、AVL树（二叉平衡搜索树）等。平衡树可以完成集合的一系列操作，时间复杂度和空间复杂度相对于“2-3树”要低，在完成集合的一系列操作中始终保持平衡，为大型数据库的组织、索引提供了一条新的途径。

  例： 搜索树结点不同插入次序，将导致不同的深度和平均查找长度ASL。

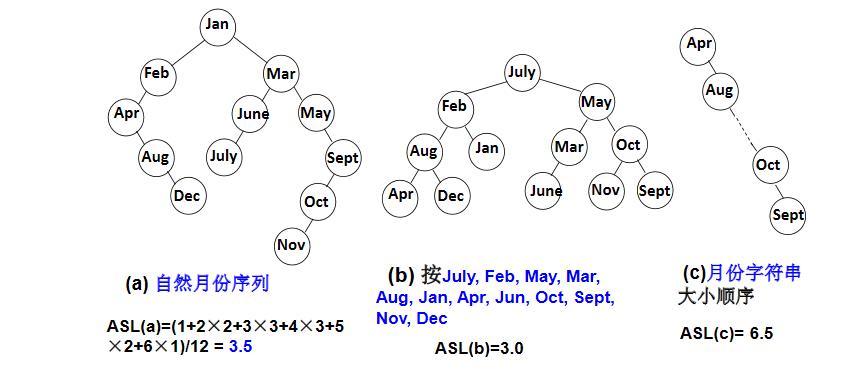
在这里插入图片描述
  “平衡因子”（Balance Factor，简称BF) ： B F ( T ) = h L − h R BF(T)= h_{L}-h_{R} BF(T)=hL​−hR​，其中 h L h_{L} hL​和 h R h_{R} hR​分别为T的左、右子树的高度。

  平衡二叉树（Balanced Binary Tree) (AVL树)： ⋆ \\star ⋆ 空树；
                        ⋆ \\star ⋆ 或者任一结点左、右子树高度差的绝对值不超过1，即 ∣ B F ( T ) ∣ ⩽ 1 |BF(T)|\\leqslant1 ∣BF(T)∣⩽1。

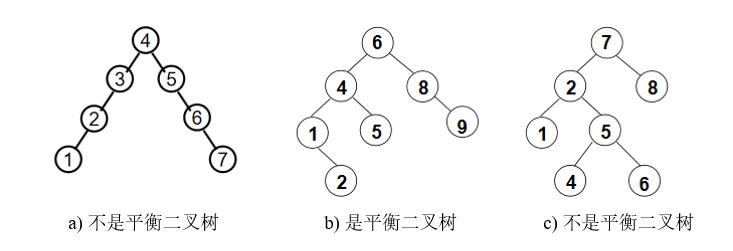
在这里插入图片描述
  平衡二叉树的目的是使得树的高度低一些，树越平衡，高度越低。

  平衡二叉树的高度能达到 l o g 2 n log_{2}n log2​n吗? l o g 2 n log_{2}n log2​n是结点为 n n n的完全二叉树的高度。

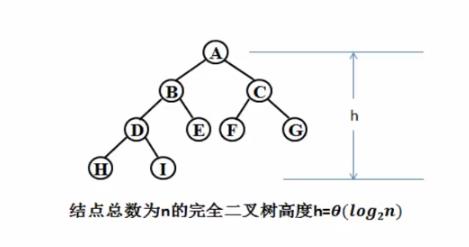
在这里插入图片描述
  设 n h n_{h} nh​是高度为 h h h的平衡二叉树的最少结点数。结点数最少时：

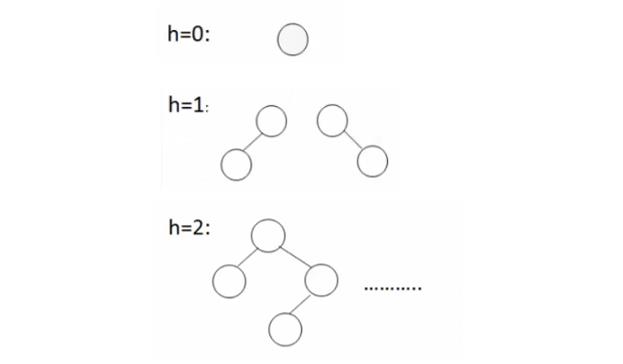
在这里插入图片描述
  可以得到如下结论：

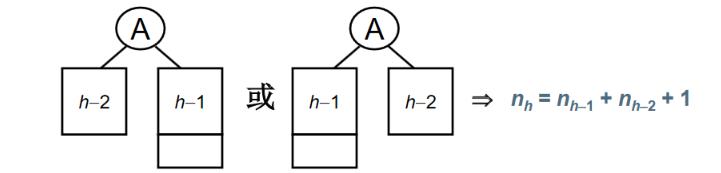
在这里插入图片描述
  斐波那契序列： F 0 = 1 , F 1 = 1 , F i = F i − 1 + F i − 2       f o r   i > 2 F_{0}=1, F_{1}=1, F_{i}=F_{i-1}+F_{i-2} \\ _{} \\ _{} \\ _{}for \\ _{} i>2 F0​=1,F1​=1,Fi​=Fi−1​+Fi−2​ ​ ​ ​for ​i>2。

在这里插入图片描述
  所以给定结点数为 n n n的AVL树的最大高度为 O ( l o g 2 n ) O(log_{2}n) O(log2​n)！

6.2 平衡二叉树的调整

6.2.1 RR旋转

  假设有下图左边所示的平衡二叉树，当在其右子树的右边插入元素Nov时二叉树变为如下图中间所示的情况，由于根结点Mar的平衡因子变为-2，所以二叉树不平衡了，需要进行调整。调整的关键是使得元素Mar、May、Nov处于平衡状态，采用RR旋转，得到下图右边所示的平衡二叉树。

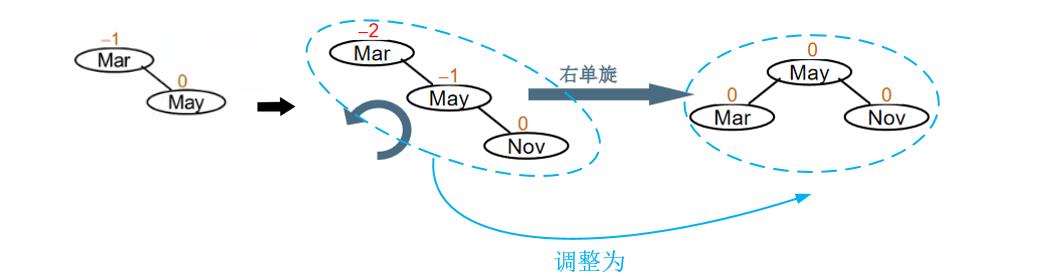
在这里插入图片描述
  不平衡的“发现者”是Mar，“麻烦结点”Nov在发现者右子树的右边，因而叫RR插入，需要RR旋转（右单旋)。

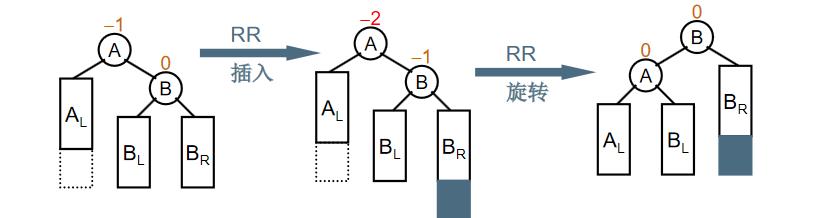
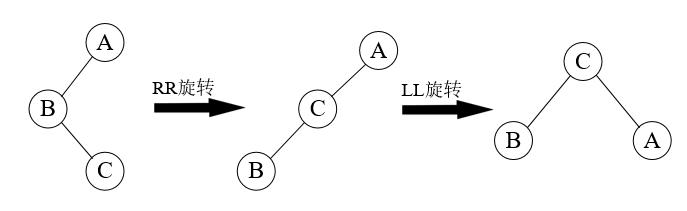
在这里插入图片描述
  RR旋转的基本思路是把B的左子树腾出来挂到A的右子树上，再将A挂在B的左子树上，返回B作为当前子树的根，如下图所示。

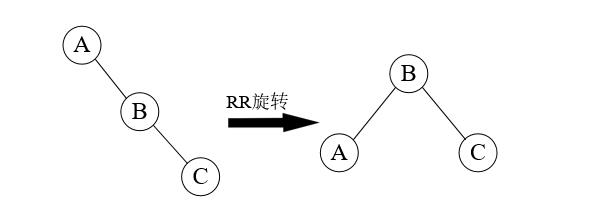
在这里插入图片描述

AVLTree RRRotation(AVLTree A)
{
    // 此时根节点是A
	AVLTree B = A->right;   // B为A的右子树  
	A->right = B->left;    // B的左子树挂在A的右子树上 
	B->left = A;   //  A挂在B的左子树上 
	return B;  // 此时B为根结点   
}

6.2.2 LL旋转

  假设有下图左边所示的平衡二叉树，当在其左子树的左边插入元素Apr时二叉树变为如下图中间所示的情况，由于左孩子结点Mar的平衡因子变为2，所以二叉树不平衡了，需要进行调整。调整的关键是使得元素Mar、Aug、Apr处于平衡状态，采用LL旋转，得到下图右边所示的平衡二叉树。

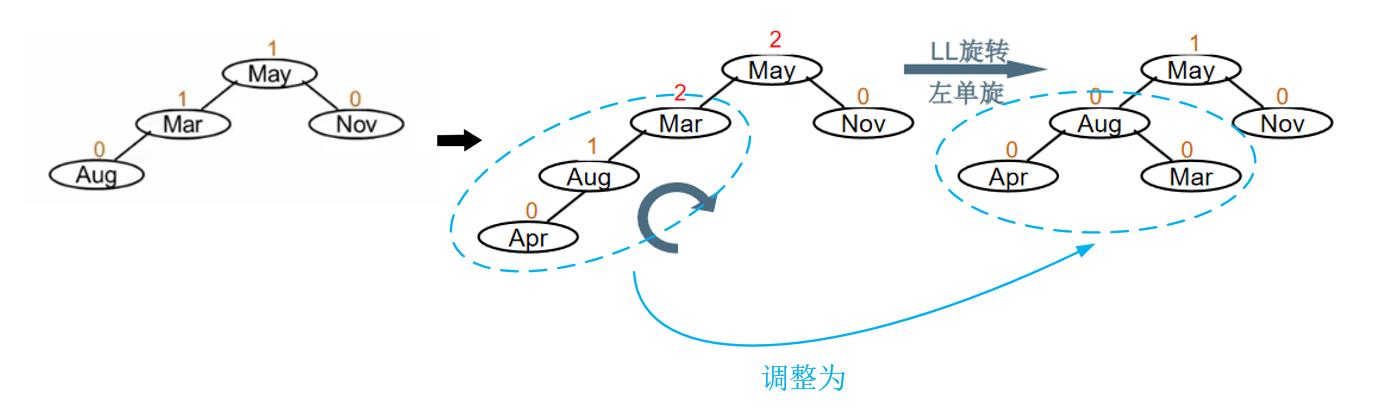
在这里插入图片描述
  不平衡的“发现者”是Mar，“麻烦结点”Apr在发现者左子树的左边，因而叫LL插入，需要LL旋转（左单旋）。

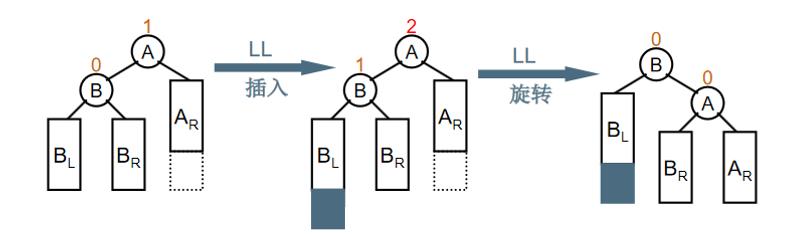
在这里插入图片描述
  LL旋转的基本思路是把B的右子树腾出来挂上A的左子树，再将A挂在B的右子树上，返回B作为当前子树的根，如下图所示。

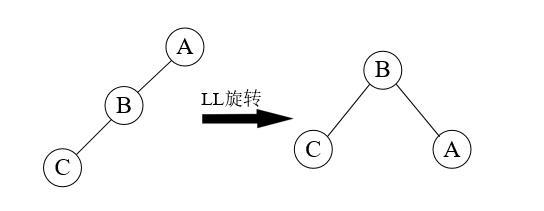
在这里插入图片描述

AVLTree LLRotation(AVLTree A)
{
	// 此时根节点是A 
	AVLTree B = A->left;  // B为A的左子树  
	A->left = B->right;   // B的右子树挂在A的左子树上 
	B->right = A;     //  A挂在B的右子树上 
	return B;  // 此时B为根结点 
}

6.2.3 LR旋转

  假设有下图左边所示的平衡二叉树，当在其左子树的右边插入元素Jan时二叉树变为如下图中间所示的情况，由于根结点May的平衡因子变为2，所以二叉树不平衡了，需要进行调整。调整的关键是使得元素May、Aug、Mar处于平衡状态，采用LR旋转，得到下图右边所示的平衡二叉树。

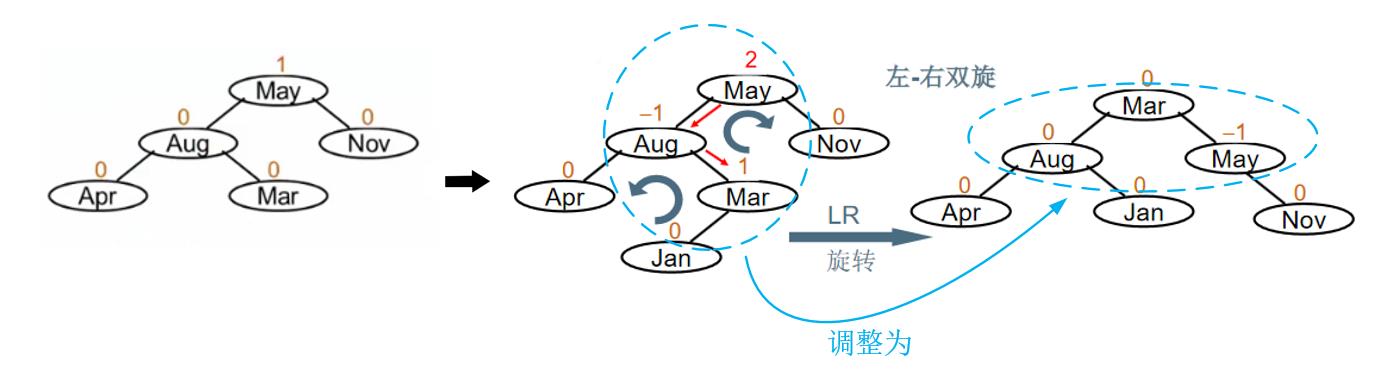
在这里插入图片描述
  不平衡的“发现者”是May，“麻烦结点”Jan在左子树的右边，因而叫LR插入，需要LR旋转。

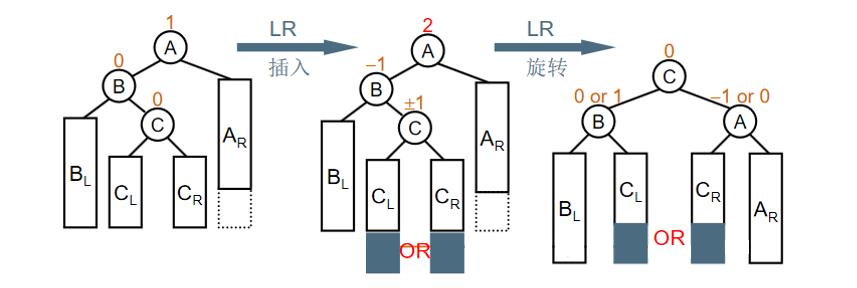
在这里插入图片描述
  LR旋转的基本思路是先将B作为根结点进行RR旋转（将C的左子树腾出来挂到B的右子树上，再将B挂在C的左子树上），再将A作为根结点进行LL旋转（把C的右子树腾出来挂到A的左子树上，再将A挂在C的右子树上），即先进行RR旋转再进行LL旋转，如下图所示。
在这里插入图片描述

AVLTree LRRotation(AVLTree A)
{
	// 先RR旋转
	A->left = RRRotation(A->left);
	// 再LL旋转 
	return LLRotation(A);
}

6.2.4 RL旋转

  假设有下图左边所示的平衡二叉树，当在其左子树结点的右边孩子节点的左边插入元素Feb时二叉树变为如下图中间所示的情况，由于左孩子结点Aug的平衡因子变为-2，所以二叉树不平衡了，需要进行调整。调整的关键是使得元素Aug、Jan、Dec处于平衡状态，采用RL旋转，得到下图右边所示的平衡二叉树。

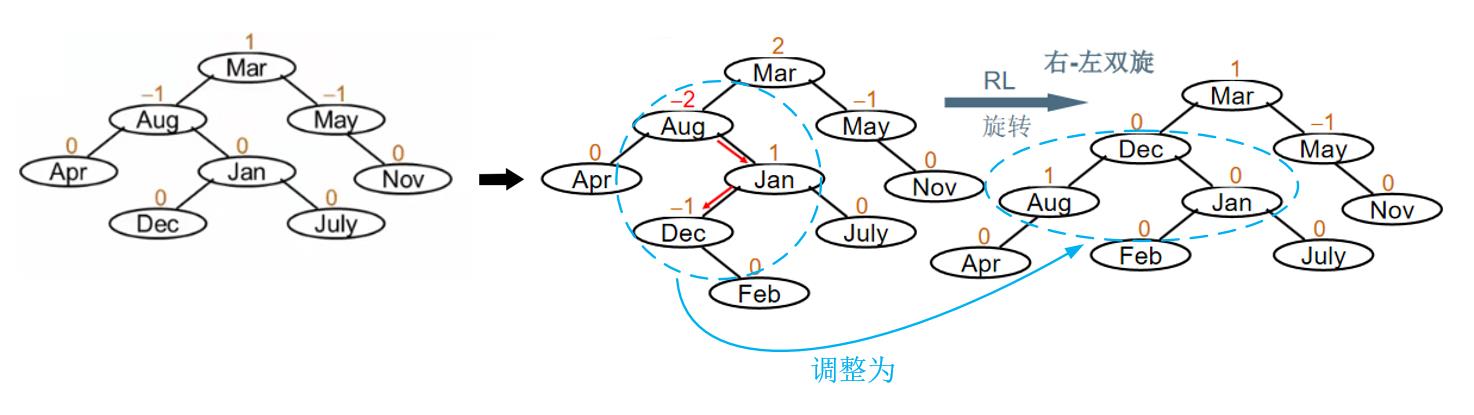
在这里插入图片描述
  一般情况调整如下图所示。

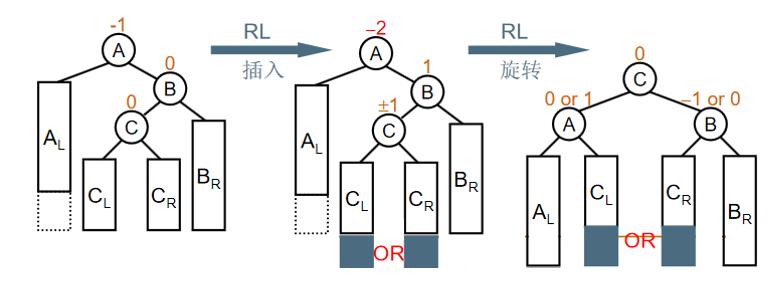
在这里插入图片描述
  RL旋转的基本思路是先将B作为根结点进行LL旋转（将C的右子树腾出来挂到B的左子树上，再将B挂在C的右子树上），再将A作为根结点进行RR旋转（将C的左子树腾出来挂到A的右子树上，再将A挂在C的左子树上），即先进行LL旋转再进行RR旋转，如下图所示。

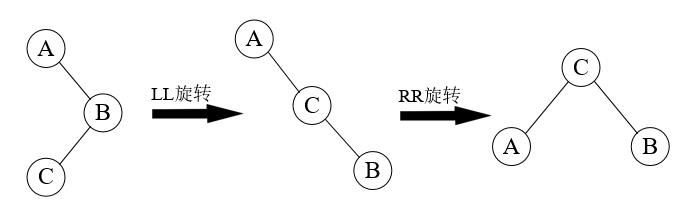
在这里插入图片描述

AVLTree RLRotation(AVLTree A)
{
	// 先LL旋转
	A->right = LLRotation(A->right);
	// 再RR旋转 
	return RRRotation(A); 
}

  综合调整的实例如下图所示。

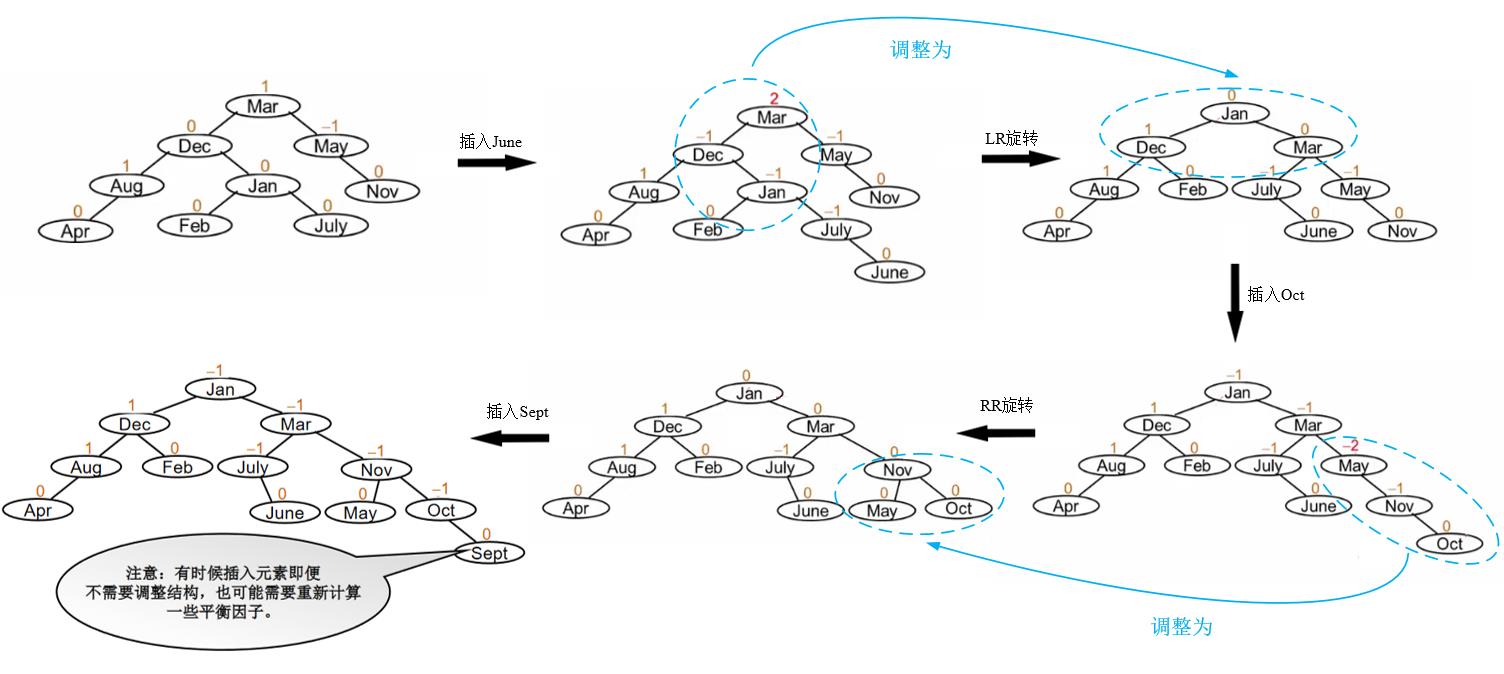
在这里插入图片描述

6.3 AVL树的根

  AVL树是一种自平衡二叉搜索树，在AVL树中任何结点的两个子树的高度最多相差1。假设由于在二叉搜索树上插入结点而失去平衡，则需要进行调整以恢复此属性，如下图所示。

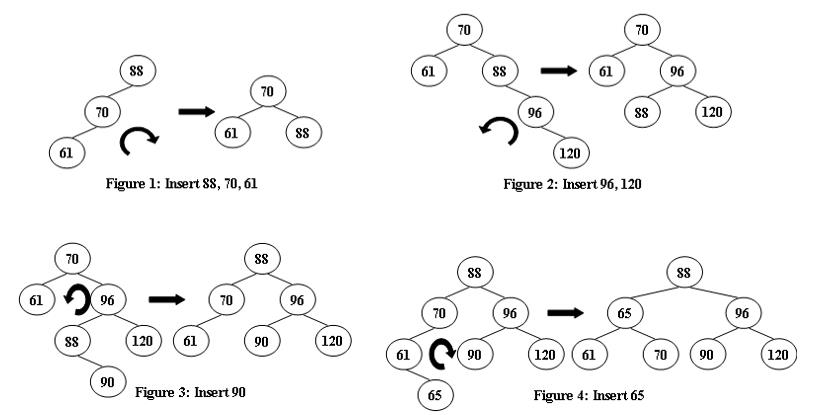
在这里插入图片描述
  现在给出了一系列的插入，需要求得AVL树的根，实现代码如下所示。

#include<iostream>
using namespace std;
typedef struct AVLNode *AVLTree;
struct AVLNode {
	int data;     // 存值 
	AVLTree left;  // 左子树 
	AVLTree right;  // 右子树 
	int height;  // 树高 
};

// 返回最大值 
int Max(int a, int b)
{
	return a > b ? a : b;
}

// 返回树高，空树返回-1 
int getHeight(AVLTree A)
{
	return A == NULL ? -1 : A->height;
}

// LL旋转
// 把B的右子树腾出来挂上A的左子树，再将A挂在B的右子树上，返回B作为当前子树的根
AVLTree LLRotation(AVLTree A)
{
	// 此时根节点是A 
	AVLTree B = A->left;  // B为A的左子树  
	A->left = B->right;  // B的右子树挂在A的左子树上 
	B->right = A;   // A挂在B的右子树上 
	A->height = Max(getHeight(A->left), getHeight(A->right)) + 1;
	B->height = Max(getHeight(B->left), A->height) + 1;
	return B;  // 此时B为根结点 
}

// RR旋转
// 把B的左子树腾出来挂到A的右子树上，再将A挂在B的左子树上，返回B作为当前子树的根
AVLTree RRRotation(AVLTree A)
{
	// 此时根节点是A 
	AVLTree B = A->right;  // B为A的右子树
	A->right = B->left;   // B的左子树挂在A的右子树上
	B->left = A;   // A挂在B的左子树上
	A->height = Max(getHeight(A->left), getHeight(A->right)) + 1;
	B->height = Max(getHeight(B->left), A->height) + 1;
	return B;  // 此时B为根结点 
}

// LR旋转 
// 先将B(A->left)作为根结点进行RR旋转，再将A作为根结点进行LL旋转
AVLTree LRRotation(AVLTree A)
{
	// 先RR旋转
	A->left = RRRotation(A->left);
	// 再LL旋转 
	return LLRotation(A);
}

// RL旋转
// 先将B(A->right)作为根结点进行LL旋转，再将A作为根结点进行RR旋转
AVLTree RLRotation(AVLTree A)
{
	// 先 LL 单旋
	A->right = LLRotation(A->right);
	// 再 RR 单旋 
	return RRRotation(A);
}

AVLTree Insert(AVLTree T, int x)
{
	if (!T)  // 如果该结点为空，初始化结点
	{
		T = (AVLTree)malloc(sizeof(struct AVLNode));
		T->data = x;
		T->left = NULL;
		T->right = NULL;
		T->height = 0;
	}
	else   // 否则不为空
	{
		if (x < T->data)  // 左子树
		{
			T->left = Insert(T->left, x);
			if (getHeight(T->left) - getHeight(T->right) == 2)   // 如果左子树和右子树高度差为 2 
			{
				if (x < T->left->data)  // LL旋转 
					T = LLRotation(T);
				else if (x > T->left->data)  // LR旋转
					T = LRRotation(T);
			}
		}
		else if (x > T->data)   // 右子树
		{
			T->right = Insert(T->right, x);
			if (getHeight(T->right) - getHeight(T->left) == 2)
			{
				if (x < T->right->data)  // RL旋转 
					T = RLRotation(T);
				else if (x > T->right->data)  // RR旋转
					T = RRRotation(T);
			}
		}
	}
	//更新树高 
	T->height = Max(getHeight(T->left), getHeight(T->right)) + 1;
	return T;
}

int main()
{
	AVLTree T = NULL;
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		int tmp;
		cin >> tmp;
		T = Insert(T, tmp);
	}
	cout << T->data << endl;
	system("pause");
	return 0;
}

  运行上述代码，进行测试。

  • 测试1：输入图2)所示的树
5
88 70 61 96 120

  代码运行的测试效果如下图所示，AVL树的根结点为70（对应图2)所示的树）。

在这里插入图片描述

  • 测试2：输入图4)的树
7
88 70 61 96 120 90 65

  代码运行的测试效果如下图所示，AVL树的根结点为88（对应图4)所示的树）。

在这里插入图片描述

以上是关于数据结构—— 树：平衡二叉树的主要内容，如果未能解决你的问题，请参考以下文章

平衡二叉树代码

平衡二叉树详解——PHP代码实现

PHP代码实现平衡二叉树详解

树--07---二叉树--04--平衡二叉树（AVL树）

判断一颗二叉树是否为二叉平衡树 python 代码

你真的懂树吗？二叉树AVL平衡二叉树伸展树B-树和B+树原理和实现代码详解...