数据结构树 —— 编程作业 01 ：树的同构

Posted 2021-06-03 大彤小忆

  题目描述： 给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树，而图2就不是同构的。

图1

图2

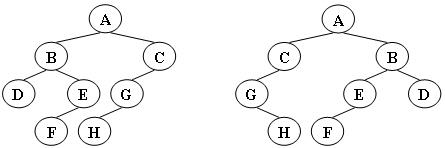
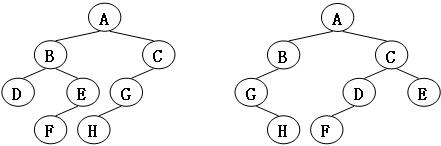
  现给定两棵树，请判断它们是否是同构的。

  输入格式： 输入给出2棵二叉树树的信息。
        对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；
        随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。
        如果孩子结点为空，则在相应位置上给出“-”。
        给出的数据间用一个空格分隔。
        注意：题目保证每个结点中存储的字母是不同的。

  输出格式： 如果两棵树是同构的，输出"Yes"，否则输出"No"。

  输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

  输出样例1：

Yes

  输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

  输出样例2：

No

  解题思路： 见数据结构（三）—— 树（4）：树的同构。

  代码实现：

#include<iostream>
using namespace std;
#define MaxTree 10
#define Null -1
#define ElementType char
#define Tree int
struct TreeNode {
	ElementType data;    // 存值 
	Tree left;   // 左子树的下标 
	Tree right;  // 右子树的下标 
}T1[MaxTree], T2[MaxTree];

// 建二叉树，返回根结点 （根节点编号未出现在其他结点编号的后面，创建一个check数组来确定）
Tree BuildTree(struct TreeNode T[])
{
	int i;
	int n;
	int check[MaxTree];  //创建一个check数组来确定根节点，若在静态链表中未出现的下标则为根节点
	char left, right;
	Tree root = Null;   //若n为0，返回Null

	cin >> n;
	if (n)
	{
		for (i = 0; i < n; i++)
		{
			check[i] = 0;
		}
		for (i = 0; i < n; i++)
		{
			cin >> T[i].data >> left >> right;
			if (left != '-')
			{
				T[i].left = left - '0';   //若输入不为'-',那字符减去字符0转换为整型数值
				check[T[i].left] = 1; //把在静态链表中出现过的数值标记为1
			}
			else if (left == '-')
				T[i].left = Null;
			if (right != '-')
			{
				T[i].right = right - '0';
				check[T[i].right] = 1;
			}
			else if (right == '-')
				T[i].right = Null;
		}

		for (i = 0; i < n; i++)
		{
			if (!check[i])
				break;
		}
		root = i;

	}
	return root;
}

// 判断是否同构
bool Isomorphic(int R1, int R2)
{
	if (R1 == Null && R2 == Null)   // 都为空 
		return true;
	if (R1 == Null && R2 != Null || R1 != Null && R2 == Null)    // 一个为空，一个不为空
		return false;
	if (T1[R1].data != T2[R2].data)   // 值不同
		return false;
	if ((T1[R1].left == Null) && (T2[R2].left == Null))  //左儿子均为空
	{
		return Isomorphic(T1[R1].right, T2[R2].right);
	}
	if ((T1[R1].left != Null && T2[R2].left != Null) && (T1[T1[R1].left].data == T2[T2[R2].left].data))  // 左儿子不为空且值相等
		return Isomorphic(T1[R1].left, T2[R2].left) && Isomorphic(T1[R1].right, T2[R2].right);
	else   // 左儿子不为空且值不等  或者 某一个左儿子为空（有可能左边和右边同构，右边和左边同构）
		return Isomorphic(T1[R1].right, T2[R2].left) && Isomorphic(T1[R1].left, T2[R2].right);
}

int main() 
{
	Tree R1, R2;
	R1 = BuildTree(T1);
	R2 = BuildTree(T2);
	if (Isomorphic(R1, R2))
		cout << "Yes" << endl;
	else
		cout << "No" << endl;

	system("pause");

	return 0;
}

  测试：

• 测试1：输入样例1的测试效果如下图所示。

• 测试2：输入样例2的测试效果如下图所示。