数据结构树 —— 编程作业 03：Tree Traversals Again

Posted 2021-06-03 大彤小忆

  题目描述： 可以使用堆栈以非递归的方式实现二叉树的中序遍历。例如，假设在遍历一棵6结点的二叉树(值从1到6)时，堆栈操作为：push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop()，然后可以从这个操作序列生成一个唯一的二叉树(如图1所示)。任务是给出这棵树的后序遍历序列。

图1

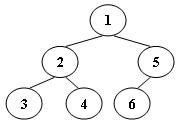
  输入格式： 每个输入文件包含一个测试用例。
        对于每个样例，第一行包含一个正整数N($⩽$ 30)，为树上的结点总数(结点编号从1到N)。
        接下来的2N行，每个描述了一个堆栈操作的格式：Push X，X是被压入堆栈的结点的索引，Pop表示从堆栈中弹出一个结点。

  输出格式： 对于每个测试用例，在一行中打印相应树的后序遍历序列。
        所有的数字必须用一个空格分隔，行尾不能有多余的空格。

  输入样例：

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

  输出样例：

3 4 2 6 5 1

  解题思路： 在输入格式中Push的顺序对应二叉树前序遍历的结果，而Pop的顺序对应二叉树中序遍历的结果。
        方法①：已知前序和中序遍历，建立一棵二叉树，然后进行后序遍历；
        方法②：已知前序和中序遍历，通过前序和中序，确定后序遍历数组的最后一位（根结点），再通过左右子树的个数和起始位置，递归确定后序遍历的每一位。

  代码实现：

• 方法1： 已知前序和中序遍历，建立一棵二叉树，然后进行后序遍历。

#include <iostream>
using namespace std;
#define MaxTree 30
#include <stack>
#include<string>

typedef struct Node {
	int data;
	struct Node *left, *right;
}Node, *Tree;

bool flag = true;//后序输出时是否输出空格 

//已知前序和中序遍历，建立一棵二叉树
Tree BuildTree(int n, int *PreOrder, int *InOrder) 
{
	if (n == 0)
		return NULL;
	Tree tree = (Tree)malloc(sizeof(Node));
	tree->data = PreOrder[0];
	tree->left = tree->right = NULL;
	int i;
	for (i = 0; i < n; i++) 
	{
		if (PreOrder[0] == InOrder[i])
			break;
	}
	int L = i;  //左子树结点点数
 	int R = n - (i + 1);  //右子树结点数
	tree->left = BuildTree(L, PreOrder + 1, InOrder);
    tree->right = BuildTree(R, PreOrder + L + 1, InOrder + L + 1);
	return tree;
}

//进行后序遍历
void PostOrder(Tree tree) 
{
	if (!tree)
		return;
	PostOrder(tree->left);
	PostOrder(tree->right);
	if (flag) 
	{
		flag = false;
		cout << tree->data;
	}
	else 
	{
		cout << " " << tree->data;
	}
}

int main() 
{
	int n, num;
	cin >> n;
	int PreOrder[MaxTree], InOrder[MaxTree];
	int p = 0, k = 0;
	string s;
	stack<int> st;
	for (int i = 0; i < 2 * n; i++) 
	{
		cin >> s;
		if (s == "Push") 
		{
			cin >> num;
			PreOrder[p++] = num;  //PreOrder中存放先序遍历的序列
			st.push(num);
		}
		else {
			InOrder[k++] = st.top();  //InOrder中存放中序遍历的序列
			st.pop();
		}
	}
	Tree tree = BuildTree(n, PreOrder, InOrder);
	PostOrder(tree);
	system("pause");
	return 0;
}

• 方法2： 已知前序和中序遍历，通过前序和中序，确定后序遍历数组的最后一位（根结点），再通过左右子树的个数和起始位置，递归确定后序遍历的每一位。

#include <iostream>
using namespace std;
#define MaxTree 30
#include <stack>
#include<string>

int pre[MaxTree], in[MaxTree], post[MaxTree];

//前序起始位置，中序起始位置，后序起始位置，元素个数
void PostOrder(int prel, int inl, int postl, int n)
{
	if (n == 0)
		return;//递归结束
	if (n == 1)
	{
		post[postl] = pre[prel];
		return;
	}
	int root = pre[prel];
	post[postl + n - 1] = root;
	int i;
	for (i = 0; i < n; i++)  //找到根在中序中的位置
	{
		if (in[inl + i] == root)
			break;
	}
	int L = i;  //左子树结点点数
	int R = n - (i + 1);  //右子树结点数
	PostOrder(prel + 1, inl, postl, L);  //建立左子树
	PostOrder(prel + L + 1, inl + L + 1, postl + L, R);  //建立右子树
}

int main()
{
	int n, num;
	cin >> n;
	int p = 0, k = 0;
	string s;
	stack<int> st;
	for (int i = 0; i < 2 * n; i++)
	{
		cin >> s;
		if (s == "Push")
		{
			cin >> num;
			pre[p++] = num;
			st.push(num);
		}
		else
		{
			in[k++] = st.top();
			st.pop();
		}
	}
	PostOrder(0, 0, 0, n);
	for (int i = 0; i < n; i++)
	{
		if (i == 0)
			cout << post[i];
		else
			cout << " " << post[i];
	}
	system("pause");
	return 0;
}

  测试： 输入样例的测试效果如下图所示。