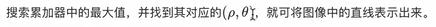Opencv-图像处理理论与实例操作

Posted 2021-06-03 胜天半月子

本节内容上接这篇博客：

• Opencv-图像操作与处理入门基本知识（一）

文章目录

• • 2.7 图像阈值与平滑处理
  • • 2.7.1 阈值处理
    • 2.7.2. 平滑处理
    • • 均值滤波
      • 方框滤波
      • 高斯滤波
  • 2.8 图像梯度 ⭐
  • • 2.8.1 Sobel算子
    • 2.8.2 Scharr算子
    • 2.8.3 laplacian算子
    • 2.8.4 边缘检测原理⭐
    • 2.8.5 Canny边缘检测⭐⭐
    • 2.8.6 图像轮廓
• 三、 直方图与傅里叶变换
• • 3.1 灰度直方图
  • • 3.1.1 掩膜的应用
  • 3.2 直方图均衡化
  • • 3.2.1 自适应的直方图均衡化
  • 3.3 傅里叶变换⭐⭐⭐
• 四、模板匹配和霍夫变换
• • 4.1 模板匹配
  • • • 匹配多个对象
  • 4.2 霍夫变化
  • • 4.2.1 原理解释
    • 4.2.2 霍夫线检测
    • 4.2.3 霍夫线检测
• 总结

笔记来源

• （全）基于python的Opencv项目实战
• 黑马程序员人工智能教程_10小时学会图像处理OpenCV入门教程

2.7 图像阈值与平滑处理

• 理解阈值

理解阈值是干什么的?

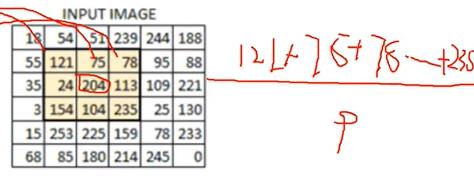
假如有如图上的像素点数值，对于每一个像素点值进行判断：该像素点大于阈值如何处理，小于阈值如何处理
这就是阈值函数要做的事情

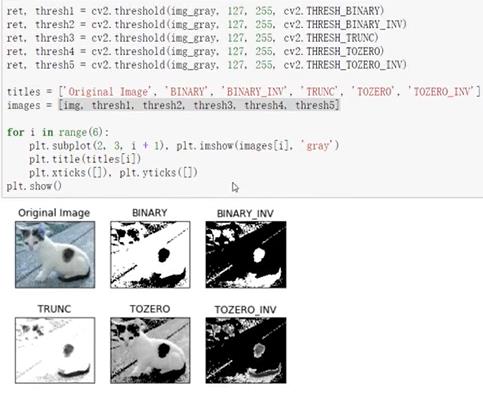
2.7.1 阈值处理

• 实例
  

2.7.2. 平滑处理

平滑处理：即滤波操作

均值滤波

方框滤波

normalize = True :会做归一化，即进行核大小的计算，再除去核大小

高斯滤波

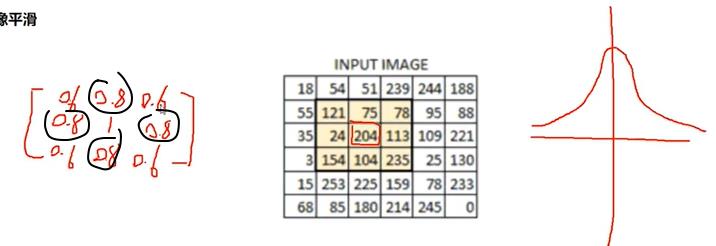
距离越近越重视，发挥的效果越好；越远发挥的效果不是那么好

• 知识博客

1. 图像与滤波
2. 高斯模糊的算法
3. 简单易懂的高斯滤波

• 中值滤波

中值：从小到大排序，找到中间的数值

• 展示所有
  
  
  

2.8 图像梯度 ⭐

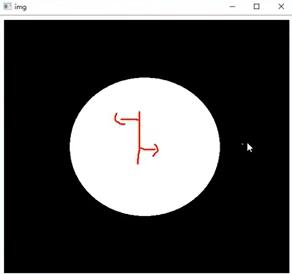
这条线左右两边都是白色一样，这条线不会产生梯度，因此边缘会产生梯度

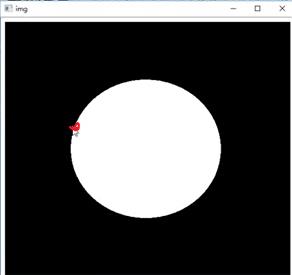
这个点左边是0（黑）右边是255（白），左右两边梯度大一些 类似边缘检测

2.8.1 Sobel算子

算法简单，实际应用效率高于canny边缘检测效率，但是准确度是低于canny的

Sobel算子是高斯平滑与微分操作的结合体：抗噪声能力强，适用于效率要求较高，细纹处理要求不高的时候

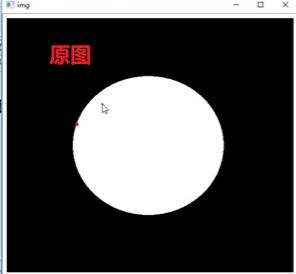
考虑水平（Gx）和竖直（Gy）两个方向
右减左，下减上

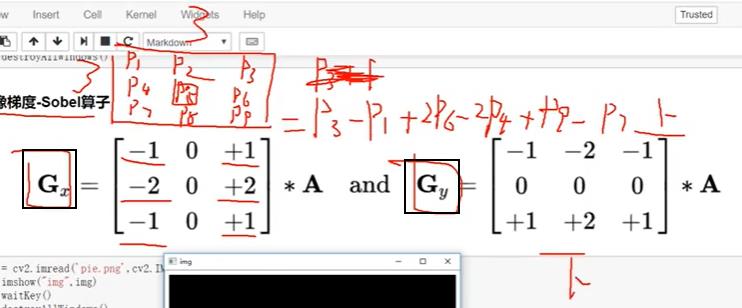
• 函数
  

将sobel算子的部分中ksize设为-1，就是利用Scharr进行边缘检测

• 实例

1. 计算水平方向
   

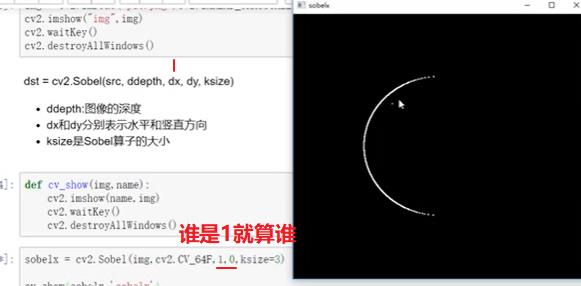
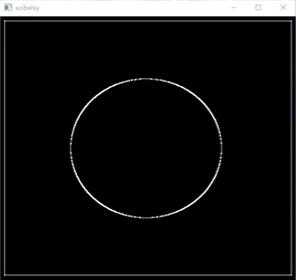
• 思考：上述图像为什么只有一半的圆？
  
  
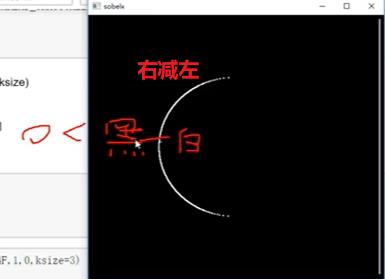
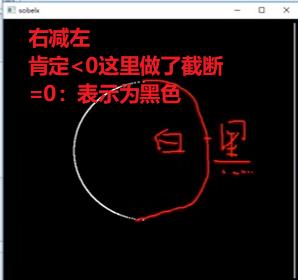
• 如何做处理让右边圆显示出来？
  
  

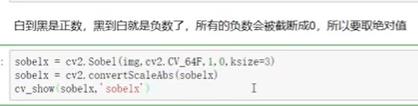
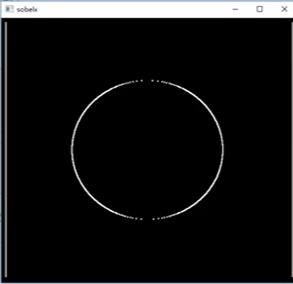
2. 计算竖直方向
   
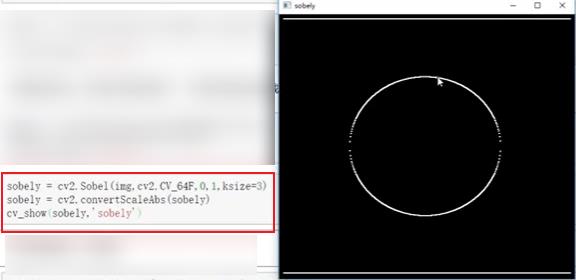
3. 计算G
   
   

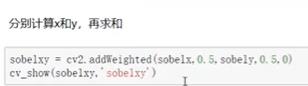
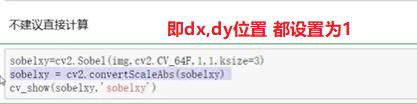
此处建议分开计算Sobelx,Sobely，再计算整体

• 整体计算
  
  

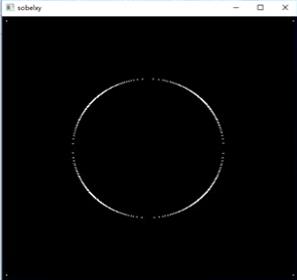
• 分开计算
  

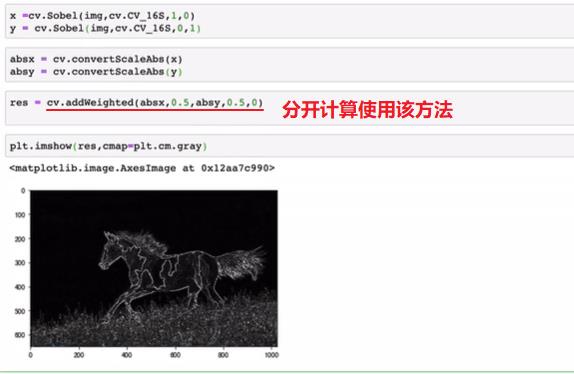
• 实例 lena图像

• 原图
  
  

• 分开计算
  

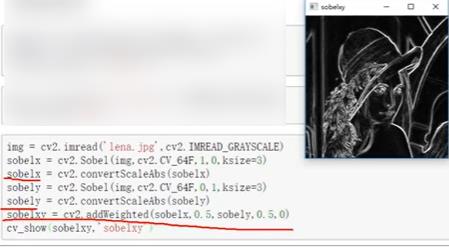
• 直接计算
  

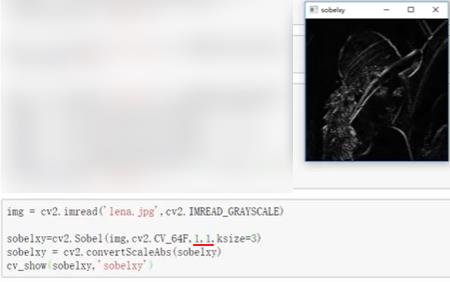
• 注意
  

2.8.2 Scharr算子

使结果差异更明显（数值更大）

2.8.3 laplacian算子

中文名称：拉普拉斯算子

对噪音点敏感，可能并不是好事，因为一些噪音点并不是一些边界

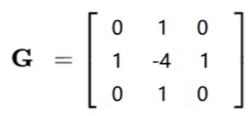
• 算子综合实例
  
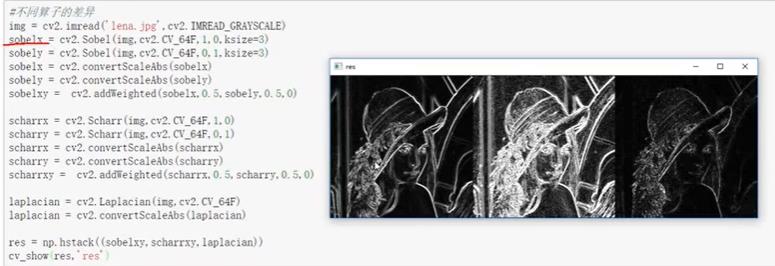
• 详细讲解

1. sobel算子，scharr算子，Laplacian算子
2. 图像边缘检测之 Sobel、Scharr、拉普拉斯算子、Canny

2.8.4 边缘检测原理⭐

边缘检测原理是图像处理和计算机视觉中的基本问题，边缘检测的目标是标识数字图像中亮度变化明显的点。
图像中属性中的显著变化通常反应了属性的重要事件和变化。

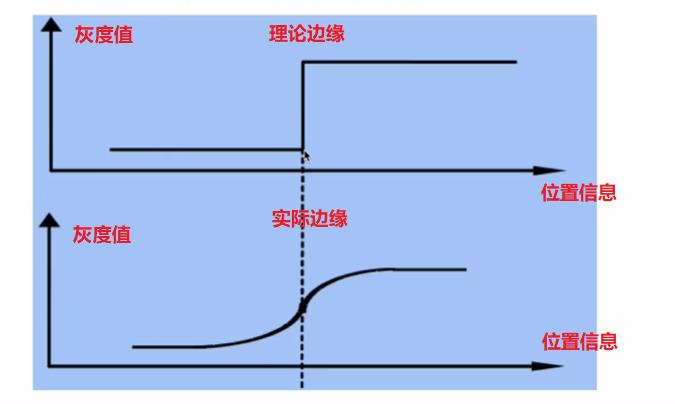
图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关地信息，保留了图像重要地结构属性。

常用的边缘检测方法可以分为两类：

1. 基于搜索
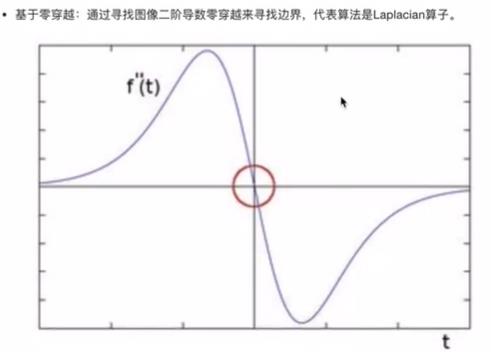
2. 基于零穿越

• 基于搜索
  
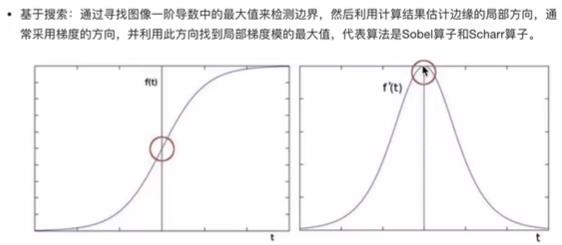
• 基于零穿越
  

2.8.5 Canny边缘检测⭐⭐

• 头衔

被认为是最优的边缘检测算法

• 算法步骤

1. 噪声去除
   由于边缘检测很容易收到噪声的影响，所以首先使用5*5高斯滤波器去除噪声【具体看平滑处理章节中的高斯滤波】
2. 计算图像梯度
   计算图像中每个像素点的梯度强度和方向
   
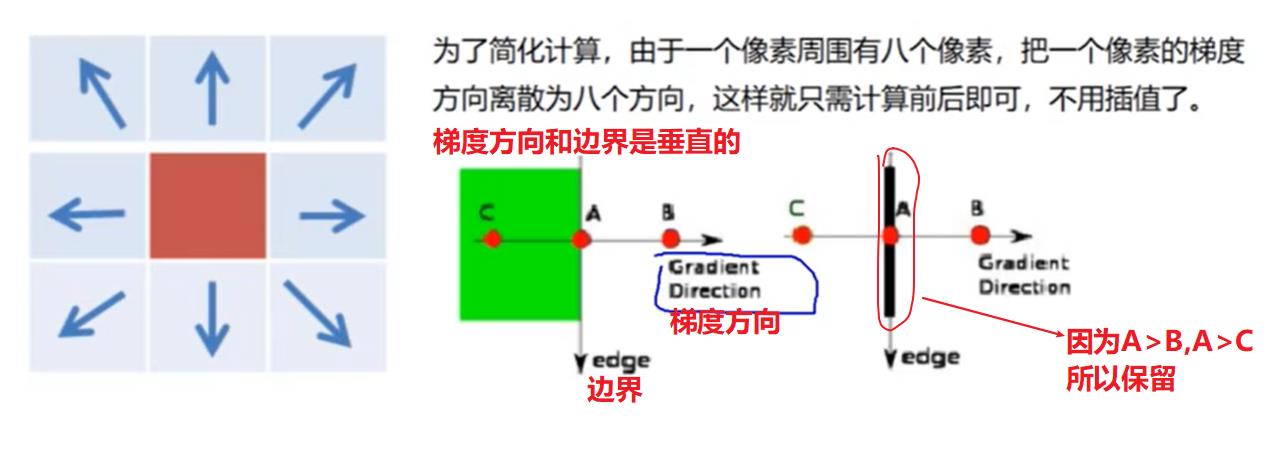
3. 非极大值抑制
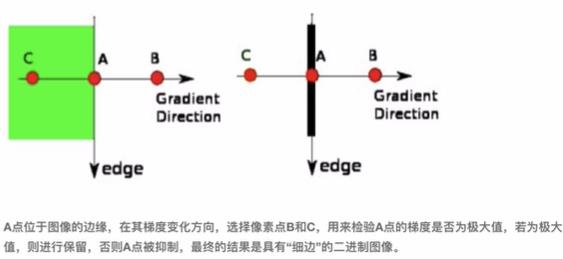
   在获得梯度的大小和方向之后，对整幅图像进行扫描，去除那些非边界上的点。对每一个像素进行检查，看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图：
   
   
   通俗讲解如上图，最后选择A-99%
4. 滞后阈值
   应用双阈值检测来确定真实的和潜在的边缘
   
5. 通过抑制孤立的弱边缘最终完成边缘检测

• 算法步骤详解

1. 高斯滤波器

高斯滤波器:中间点比较大，边缘比较小

2. 梯度和方向

使用的Sobel算子
具体看图像梯度中的Sobel算子

3. 非极大值抑制

• 方法一
  
• 方法二
  

4. 双阈值检测
   

minval取值较小：希望检测的边界尽可能多，但是结果可能是不是边界的也认为成边界；minval取值较大，要求高，只有极为边界的时候才有可能拿出来

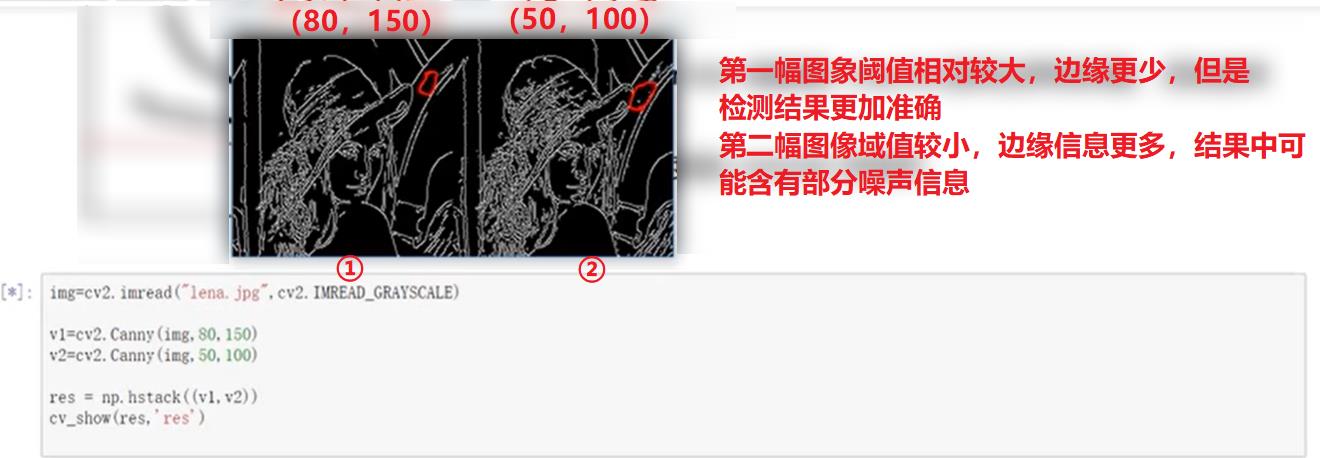
综上两幅图像，阈值大小的设定要自己进行测试，并不是越大或者越小合适

• API

canny = cv2.Canny(image,threshold1,threshold2)
参数：

• image：灰度图
• threshold1：minval较小的阈值将间断的边缘连接起来
• threshold2：maxval较大的阈值检测图像中明显的边缘

• 示例

import cv2 as cv
import numpy as np

path = 图片路径
img = cv.imread(path)

# 边缘检测
lowThreshold = 0   # minval
max_lowThreshold = 100   #maxval
canny = cv.Canny(img,lowThreshold,max_lowThreshold )

# 图像显示
...

• 算子比较
  

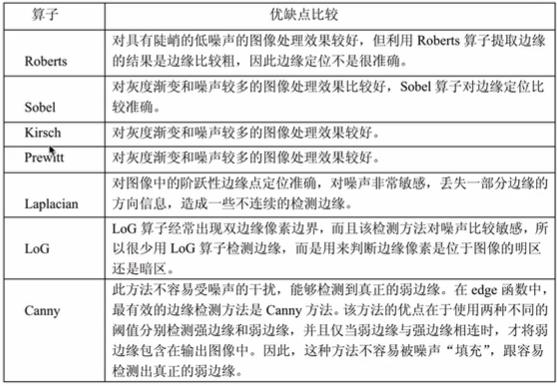
2.8.6 图像轮廓

• 什么叫轮廓

先前边缘检测的部分是零零散散的线段，不能称之为轮廓。轮廓应该是整体，连接在一起的是轮廓。

• API
  
  

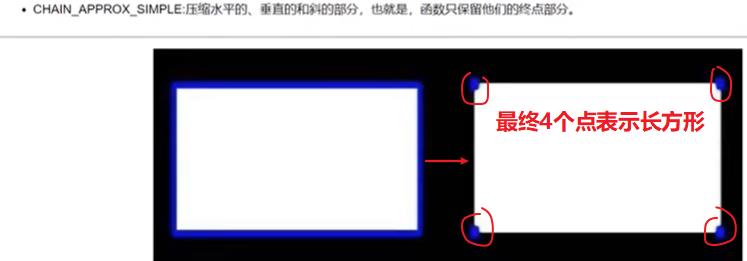
为了更高的准确率，使用二值图像

• 步骤⭐

1. 读取数据
2. 转换为灰度图
3. 图像阈值处理（对图像数据进行二值处理）
4. 调用轮廓检测函数

• 原图
  
• 处理结果图
  
• 步骤解析
  
  
  

保存的是轮廓信息

• 绘制轮廓

直接使用cv.inread()读取的原图想绘制轮廓

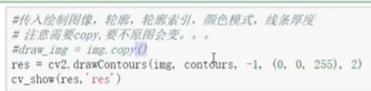
该方法中的参数 -1自己测试即可

注意此时再进行原图像展示：

因此，需要复制img,img_ = img.copy()

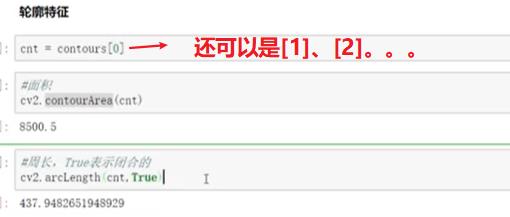
• 轮廓特征

可以进行图片中每一个轮廓的面积

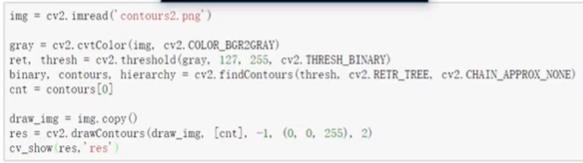
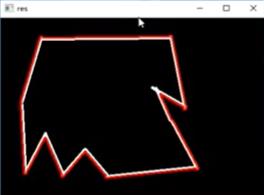
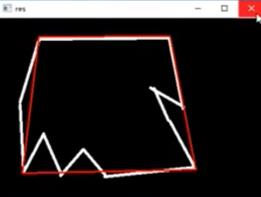
• 轮廓近似

将曲线可以近似成直线，类似将一条曲线不断地近似成直线，如果一条直线不可以，则两条、三条、直到可以。。

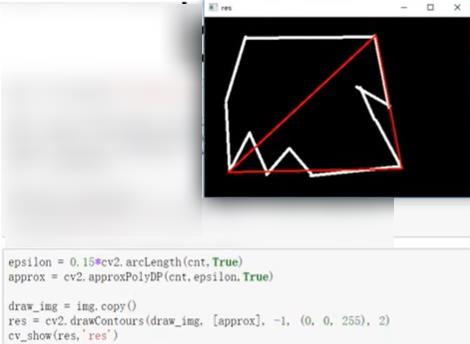
• 边界矩形
  
  
  
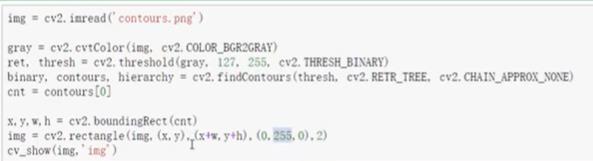
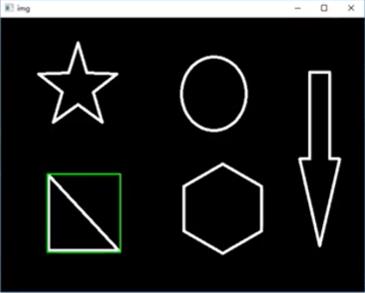
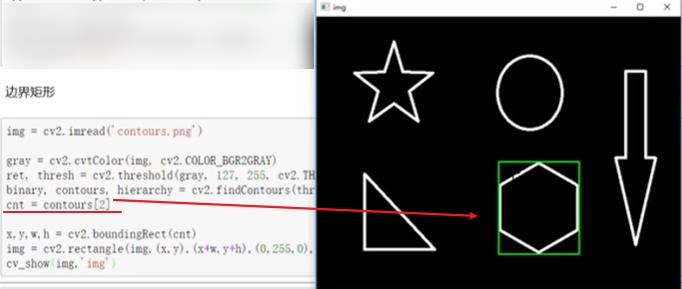
• 外接圆
  

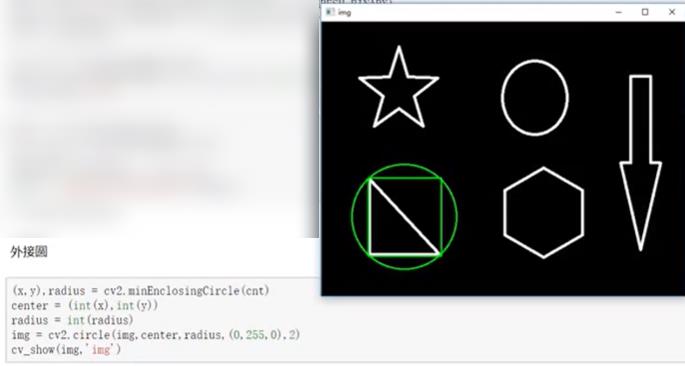
三、 直方图与傅里叶变换

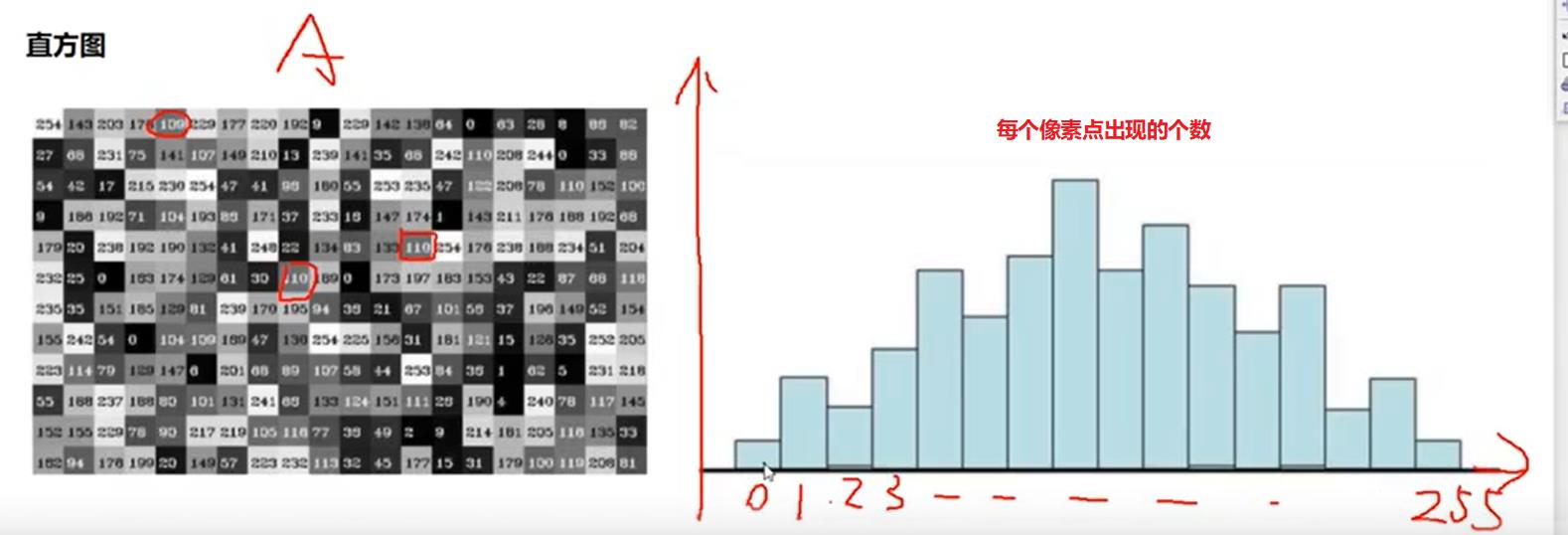
3.1 灰度直方图

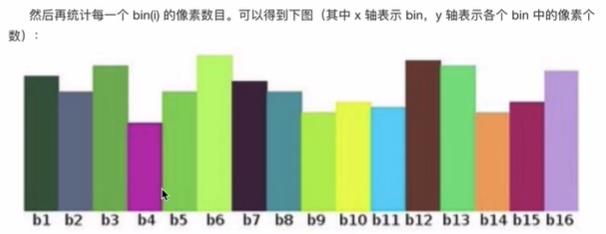
直方图是对数据进行统计的一种方法，并且将统计值组织到一系列实现定义好的bin当中.其中，bin为直方图中经常用到的一个概念，可以译为“直条”或“组距"，其致值是从数据中计算出的特征统计量，这些数据可以是诸如梯度、方向、色彩或任何其他特征。
图像直方图（Image Histogram）是用以表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素个数。
这种直方图中，横坐标的左侧为较暗的区域，而右侧为较亮的区域。因此一张较暗图片的直方图中的数据多集中于左侧和中间部分，而整体明亮、只有少量阴影的图像则相反。

注意：直方图是根据灰度图进行绘制的，而不是彩色图像。假设有一张图像的信息（灰度值0-255，已知数字的范围包含256个值，于是可以按一定规律将这个范围分割成子区域（也就是bins）
[0, 255) = [0, 15] U ]16, 30] …U [240, 255]

• 直方图的一些术语和细节：

• dims：需要统计的特征数目。在上例中，dims =1，因为仅仅统计了灰度值；要统计RGB三色的即dims = 3
• bins：每个特征空间子区段的数目，可译为“直条"或“组距”，在上例中，bins = 16.
• range：要统计特征的取值范围。在上例中，range =[0，255].

• 直方图的意义：

• 直方图是图像中像素强度分布的图形表达方式。
• 它统计了每一个强度值所具有的像素个数
• 不同的图像的直方图可能是相同的

cv2.calcHist(images,channels,mask,histSize,ranges[,hist[,accumualte]])

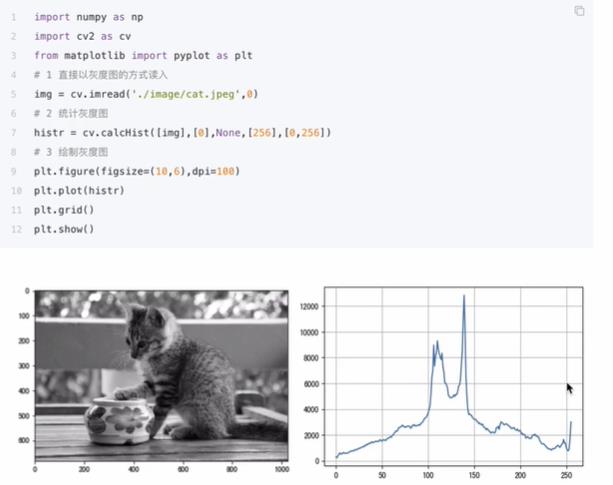
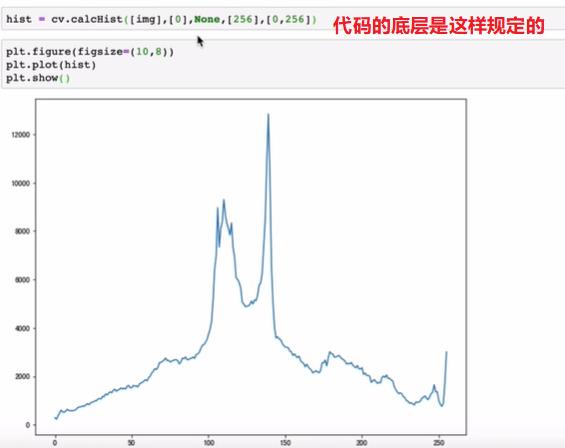
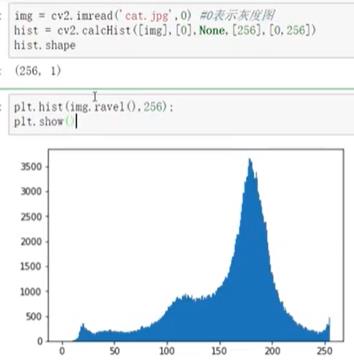
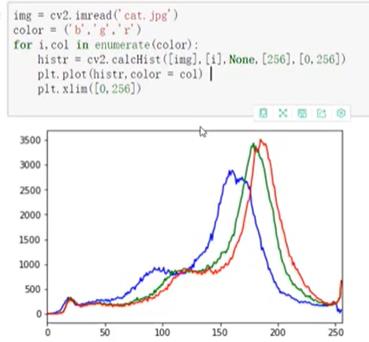
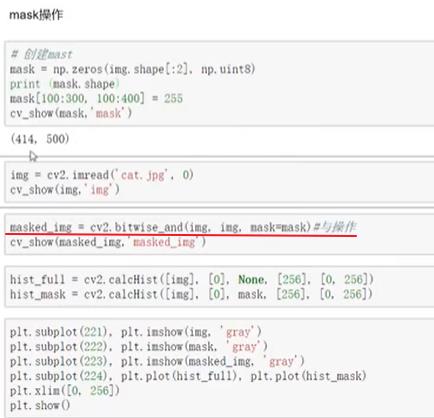
3.1.1 掩膜的应用

• 示例一

# 创建掩膜
mask = np.zeros(img.shape[:2],np.unit8)
mask[400:650,200,500] = 1

plt.imshow(mask,cmap=plt.cm.gray)

mask_img = cv.bitwize_and(img,img,mask=maks) # 与操作

plt.imshow(mask_img ,cmap=plt.cm.gray)

mask_hist = cv.calcHist([img],[0],mask,[256],[0,256])
plt.plot(mask_hist) # 折线图
plt.show()

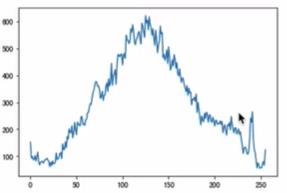
• img.shape[:2]问题

img.shape[:2] 表示取彩色图片的长、宽。
img.shape[:3] 则表示取彩色图片的长、宽、通道。

关于img.shape[0]、[1]、[2]
img.shape[0]:图像的垂直尺寸（高度）
img.shape[1]:图像的水平尺寸（宽度）
img.shape[2]:图像的通道数

在矩阵中，[0]就表示行数，[1]则表示列数


import cv2
image=cv2.imread("D:/shape.bmp")
print(image.shape[0])
print(image.shape[1])
print(image.shape[2])
结果
300
200
3

• 示例二
  

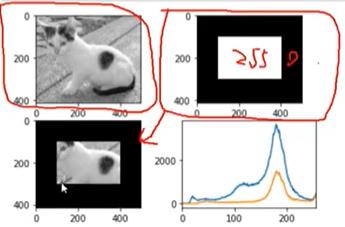
如何获得上述图像？
要保存图像的部分设置为255：mask[100:300,100:400] = 255

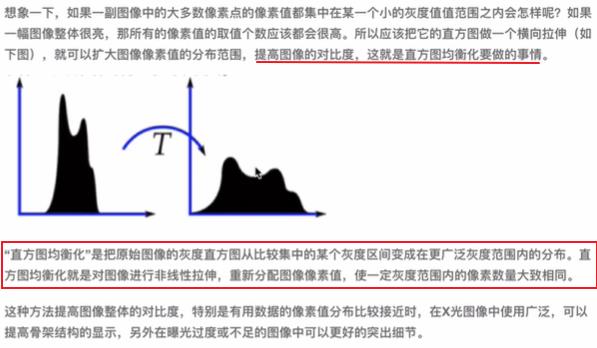
3.2 直方图均衡化

1. 原理与应用
   
   

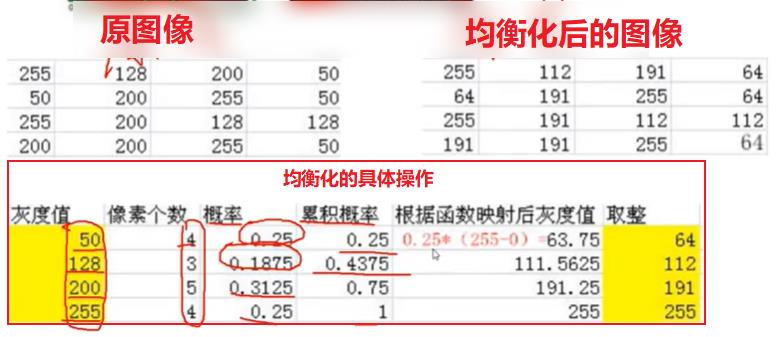
• API

dist = cv.equalizeHist(img)

• 示例

dist = cv.equalizeHist(img)
plt.inshow(dist,cmap=plt.cm.gray) # 均衡化图像
plt.inshow(img,cmap=plt.cm.gray)  # 原始图像

有些地方会更亮，有些地方也会变暗（例如猫退或者猫尾）

3.2.1 自适应的直方图均衡化

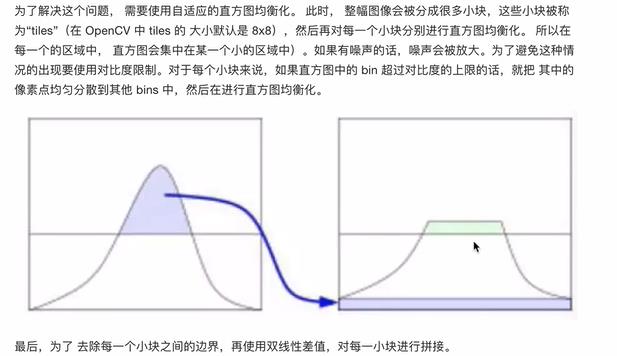
• API

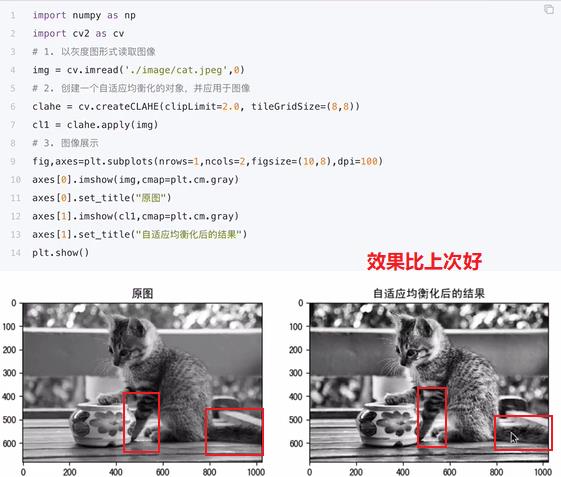
cv.createCLAHE(clipLimit,tileGridSize)
参数：clipLimit：对比度限制，默认是40
	  tileGridSize：分块的大小，默认8*8

• 小结
  
• 局部直方图均衡化效果⭐
  

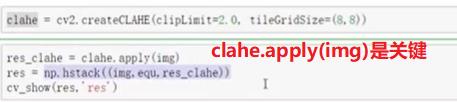
calhe.apply(img) :对img进行限制对比度自适应直方图均衡化

• 参考博客

1. 【图像增强】CLAHE 限制对比度自适应直方图均衡化
2. Python+OpenCV图像处理（八）—— 图像直方图
3. OpenCV-Python学习—对比度增强

3.3 傅里叶变换⭐⭐⭐

我们生活在时间的世界中，早上7：00起来吃早饭，8：00去挤地铁，9：00开始上班…以时间为参照就是时域分析。
但是在频域中一切都是静止的！

傅里叶分析之掐死教程

• 傅里叶变换的作用

• 高频：变化刚烈的灰度分量，例如边界（变化剧烈的是高频）
• 低频：变化缓慢的灰度分量，例如一片大海（变换缓慢的是低频）

• 滤波

• 低通滤波器：只保留低频，会使得图像模糊
• 高通滤波器：只保留高频，会使得图像细节增强

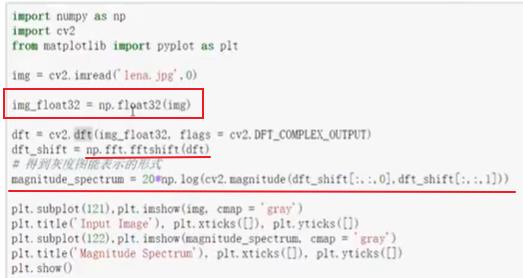
• opencv中主要就是cv2.dft()（和cv2.idft()-逆变换），输入图像需要先转换成np.fioat32格式
• 得到的结果中频率为0的部分会在左上角，通常要转换到中心位置，可以通过shift变换来实现.
• cv2.dt()返回的结果是双通道的（实部，虚部）,通常还需要转换成图像格式才能展示（0,255)

• 案例展示
• 低频显示
  
  
• 低通滤波器
  
  
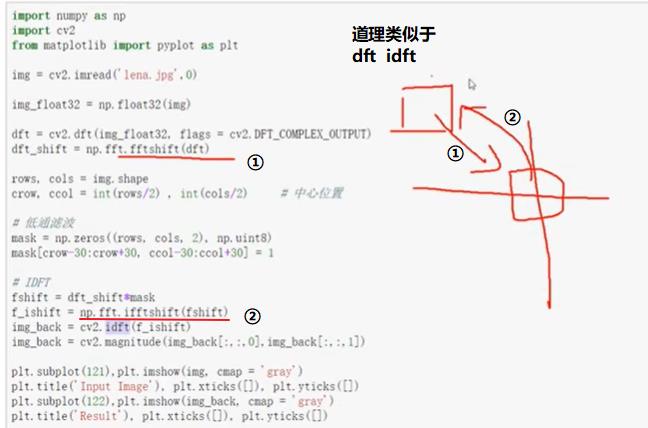
• 高通滤波器
  
  
  

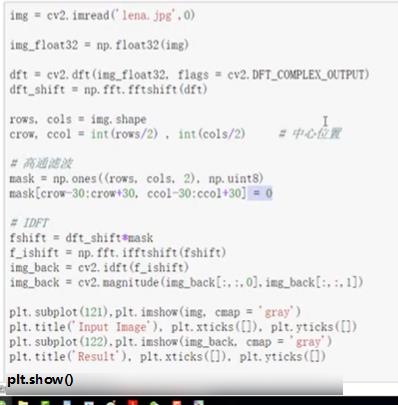
高通滤波器只保留了一些边界信息，没有留下一些细节信息

至此为止，我仍未理解傅里叶变换😳，若有通俗易懂的教程，欢迎留言，万分感谢🤝

四、模板匹配和霍夫变换

4.1 模板匹配

方向：从左到右，从上到小

• 概念原理

模板匹配：在给定的图片中查找和模板最相似的区域，该算法的输入包括模板和图片，整个任务的思路就是按照滑窗的思路不断地移动模板图片，计算其与图像中对应区域的匹配度【与机器学习中的相似度概念类似】，最终将匹配度最高地区域选为最终的结果。

• 实现流程

1. 准备两幅图像

• 原图像：在这幅图中，找到与模板匹配的区域
• 模板：与原图像进行对比的图像块

2. 滑动模板图像和原图进行比对：
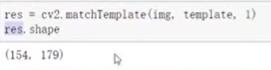
   将模板快每次移动一个像素【从左到右，从上至下】，在每一个位置，都计算与模板图像的相似度
3. 对于每一个位置将计算的相似结果保存在结果矩阵（R）中。如果输入图像的大小（WH），模板图像的大小（wh），则输出矩阵R的大小为（W-w+1,H-h+1）将R 显示为图像。
   
   
4. 获得R后，查找最大值所在的位置，那么该位置对应的区域就被认为是最匹配的。对应的区域就是以该点为顶点，长宽和模板图像一样大小的矩阵。

• API

res = cv.matchTemplate(img,tempate,method)
参数：
img ：进行模板匹配的图像
Template :模板
method:实现模板匹配的算法：

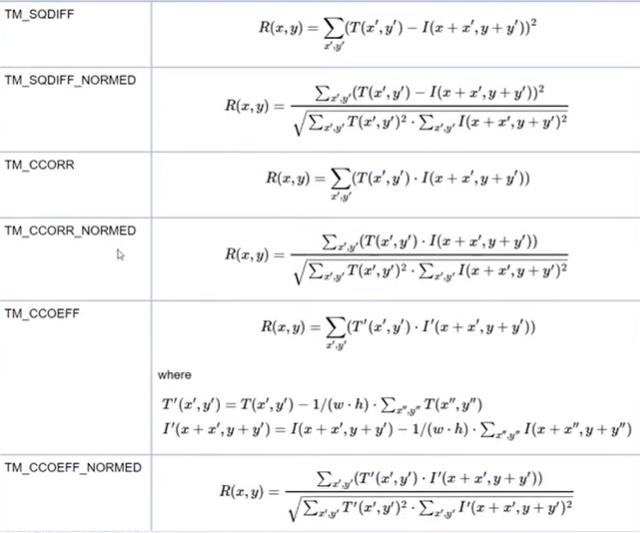
• 测试所有方法
  
  

• 示例：

1. 原图像
   
2. 模板图像
   

• 示例

import cv2 as cv
import numpy as  np

path_ori = 原图像路径
path_com = 模板图像路径

img = cv.imread(path_ori )
template = cv.imreda(path_com )

h,w,l = template.shape

# 模板匹配
res = cv.matchTemplate(img,template,cv.TM_CCORR) # 使用相关系数匹配 得到结果矩阵
# 返回图像中最匹配的位置 确定左上角的坐标，并将匹配位置绘制在图像上
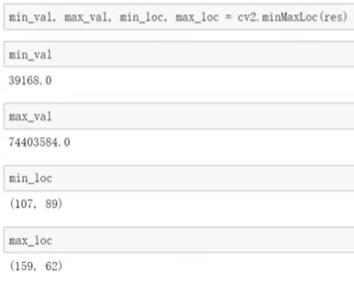
min_val,max_val,min_loc,max_loc = cv.minMaxLoc(res)# 最小值  最大值  最小位置 最大位置

top_left = max_loc # 最大位置是最好的位置   top_left 左上角位置
bottom_right = (top_left[0]+w,top_left[1]+h)  # 右下角位置
cv.rectangle(img,top_left,bottom_right ,(0,255,0),2)

# 显示图像
plt.imshow(img[:,:,::-1])
plt.show()

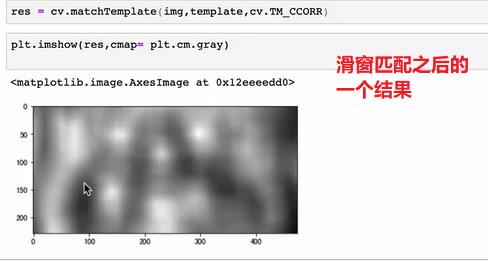
• 注意

模板匹配不适用于尺度变换，视角变换后的图像，这时我们就要使用关键点匹配算法，比较经典的关键点检测算法包括SIFT和SURF等，主要的思路是首先通过关键点检测算法获取模板和测试图片中的关键点；然后使用关键点匹配算法处理即可，这壁关键点可以很好的处理尺度变化、视角变换、旋转变化、光照变化等，具有很好的不变性。

匹配多个对象

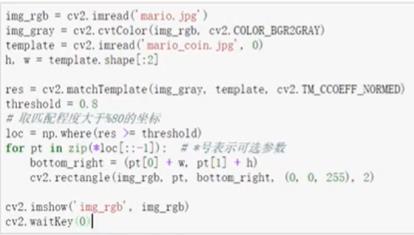
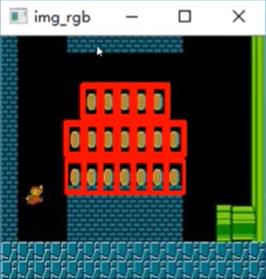
4.2 霍夫变化

• 用途

霍夫变化常用来提取图像中的直线和圆等几何形状

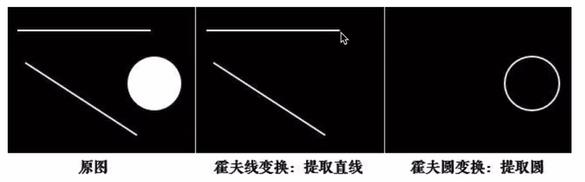
4.2.1 原理解释

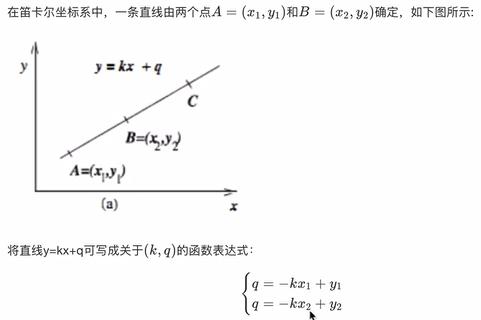
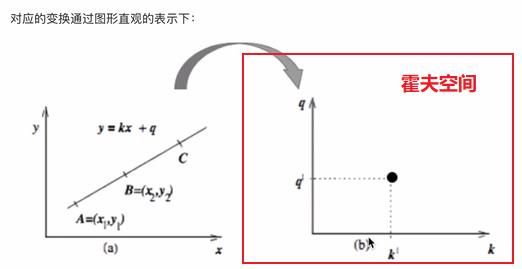
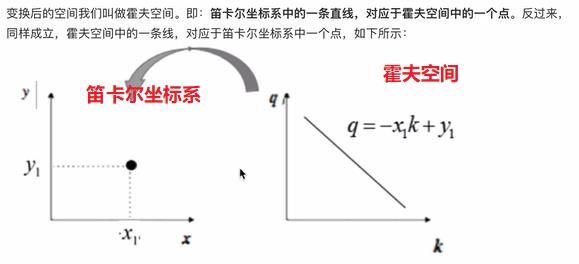
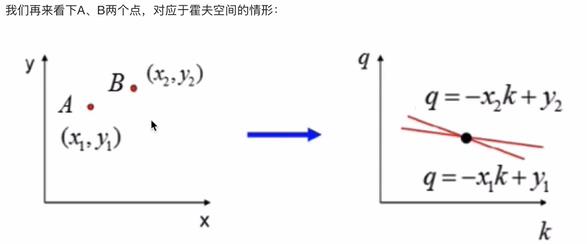
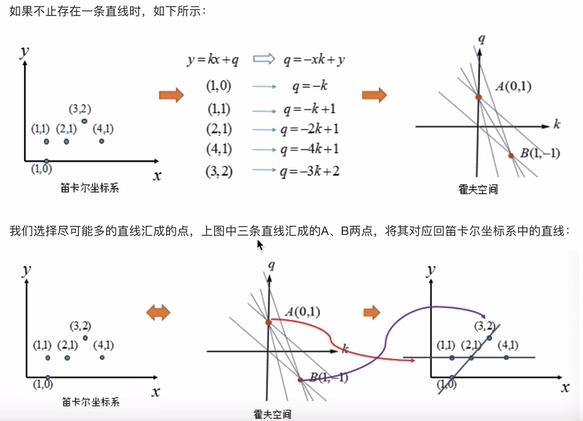
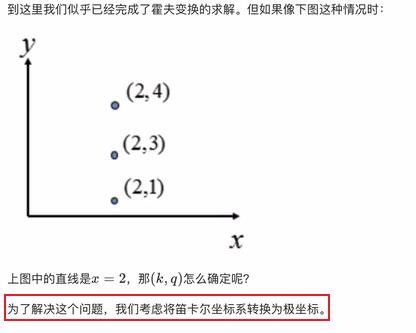
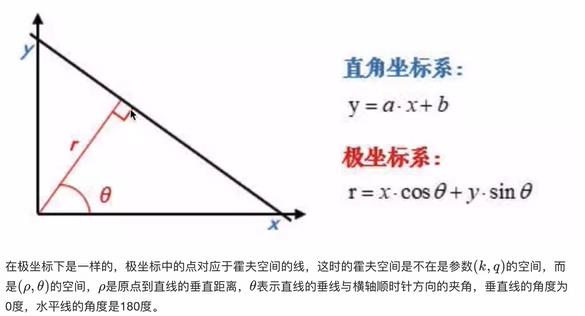
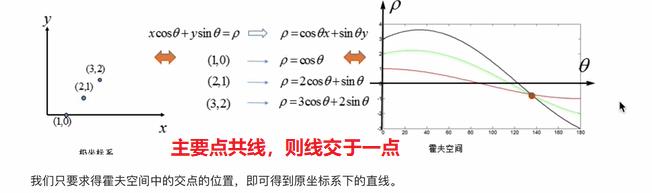
• 实现流程

假设有100*100的图片，使用霍夫变换检测图片中的线，步骤如下：

1. 
2. 
3. 
4. 

4.2.2 霍夫线检测

• API

cv2.HoughLines(img,rho,theta,threshold)
参数：

• img：二值化推向或者进行Canny边缘检测
• rho、theta：ρ和θ的精确度
• threshold：阈值，只有累加器中的值高于该值时才被认为是直线

• 示例

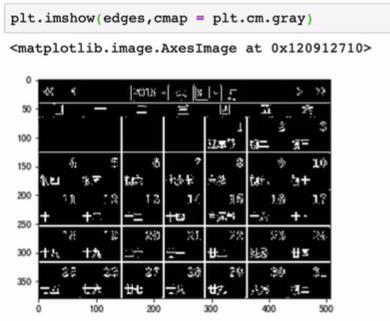
检测下图中的直线

import numpy as np
import random
import cv2 as cv

# 转换为二值图
path = 图片路径
img = cv.imread(path)

gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
edged = cv.Canny(gray,50,150) 

# 霍夫直线变换
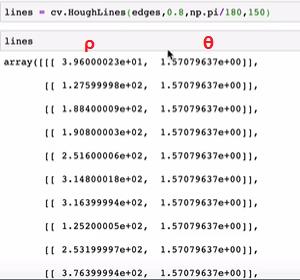
lines = cv.HoughLines(edges,0.8,np.pi/100,150) # 返回检测到的所有直线

# 绘制图像 极坐标 -》 笛卡尔
for line in lines:
	rho,theta = line[0]
	a = np.cos(theta)
	b = np.sin(theta)
	x0 = a*rho
	y0 = b*rho
	x1 = int(x0+1000(-b))
	y1 = int(y0+1000(a))
	x2 = int(x0-1000(-b))
	y2 = int(y0-1000(a))
	cv.line(img,(x1,y1),(x2,y2),(0,255,0)) # 绿色线

4.2.3 霍夫线检测

注意：霍夫圆检测对噪声比较敏感，首先应该进行中值滤波

• 检测原理
  
• API
  

import cv2 as cv
import  numpy as np

path = 图片路径
img = cv.imread(path)
gry_img = cv.cvtColor(planets,cv.COLOR2GRAY)

# 中值滤波   去除噪点
img = cv.medianBlur(gay_img,7)

# 霍夫圆检测
circles = cv.HoughCircles(img,cv.HOUGH_GRADIENT,1,200,PARAM1=100,PARAM2=30,minRadius=0 ,minRadius=100 )

# 绘制结果
for i in ciecles[0,:]:
	# 绘制圆形
	cv.circle(planets,(i[0以上是关于Opencv-图像处理理论与实例操作的主要内容，如果未能解决你的问题，请参考以下文章
 
 在 Python 多处理进程中运行较慢的 OpenCV 代码片段
 OpenCV 图像混合
 OpenCV 图像混合
 OpenCV 调整图像亮度与对比度
 OpenCV 调整图像亮度与对比度
 opencv 4 -- 图像平滑与滤波--理论解释