《信息与编码》考试复习笔记4----第四章离散信道容量
Posted 遗忘丶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《信息与编码》考试复习笔记4----第四章离散信道容量相关的知识,希望对你有一定的参考价值。
系列文章链接目录
一、《信息与编码》考试复习笔记1----第一章概论
二、《信息与编码》考试复习笔记2----第二章离散信息源
三、《信息与编码》考试复习笔记2----第二章离散信息源相关例题
四、《信息与编码》考试复习笔记3----第三章无失真离散信源编码(重要)
五、《信息与编码》考试复习笔记3----第三章无失真离散信源编码补充例题
六、《信息与编码》考试复习笔记4----第四章离散信道容量
七、《信息与编码》考试复习笔记4----第四章离散信道容量相关例题
八、《信息与编码》考试复习笔记5----第五章纠错编码(难点)
九、《信息与编码》考试复习笔记5----第五章纠错编码相关例题(难点)
十、《信息与编码》考试复习笔记----前五章题目补充
十一、《信息与编码》考试复习笔记5----第五章纠错编码–伴随式纠错译码及标准阵列译码补充(难点)
十二、《信息与编码》考试复习笔记6----第六章连续信源熵和信道容量(考点在连续信道容量)
十三、《信息与编码》考试复习笔记6----第六章连续信源熵和信道容量相关例题
十四、《信息与编码》考试复习笔记7----第七章信息率失真函数(有计算无难度)
十五、《信息与编码》考试复习笔记7----第七章信息率失真函数相关例题
文章目录
前言
这门课复习的时候有点学不进去,打算以此记录复习过程,也算加深一下印象,与大家一起学习。
本章的复习重点主要在互信息量、离散信道容量相关的计算。
一、互信息量

二、平均互信息量
2.1平均互信息量的定义

2.2平均互信息量的物理意义
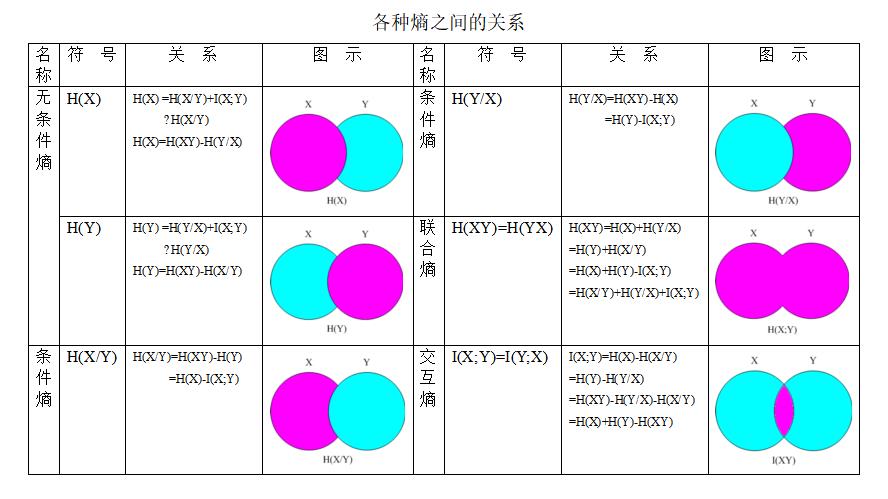
平均互信息量的三种不同形式的表达式:
(1)从接收端观察:I(X;Y) = H(X) - H(X/Y)
(2)从发送端观察:I(Y;X) = H(Y) - H(Y/X)
(3)从外部观察通信系统整体:I(X;Y) = H(X)+H(Y) - H(XY)
其中H(X/Y)又称为疑义度,H(Y/X)又称为噪声熵。H(XY)是联合熵。
2.3平均互信息量的性质
① 对称性
② 非负性
③ 极值性
④凸函数性

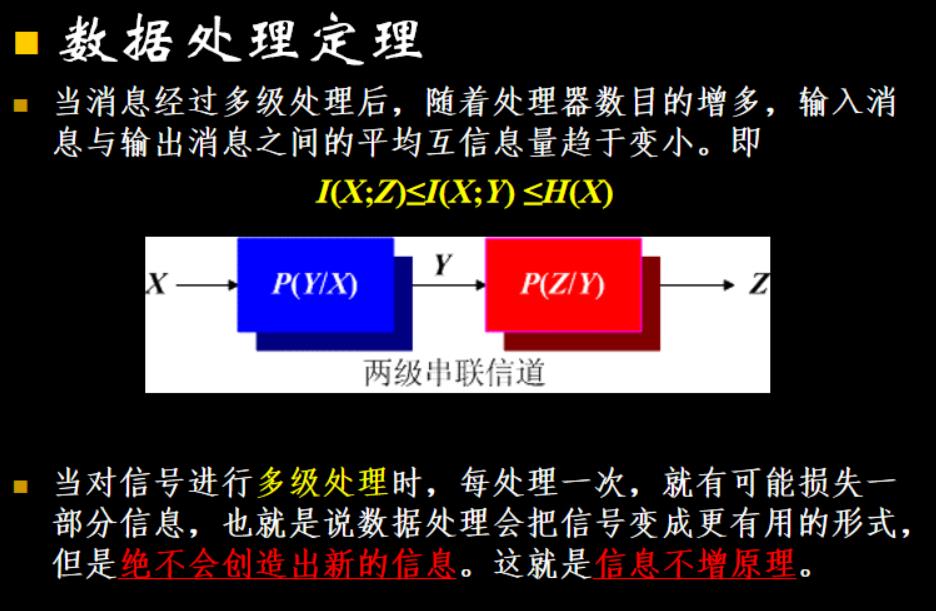
⑤ 数据处理定理
数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量趋于变小。
2.4各种熵之间的关系(重要)
三、单符号离散信道的信道容量

3.1几种特殊离散信道的信道容量

3.1.1具有一一对应关系的无噪信道
这种信道的特点是输入X和输出Y符号集的元素个数相等。信道矩阵中的元素均是1或0,X和Y有确定的对应关系。
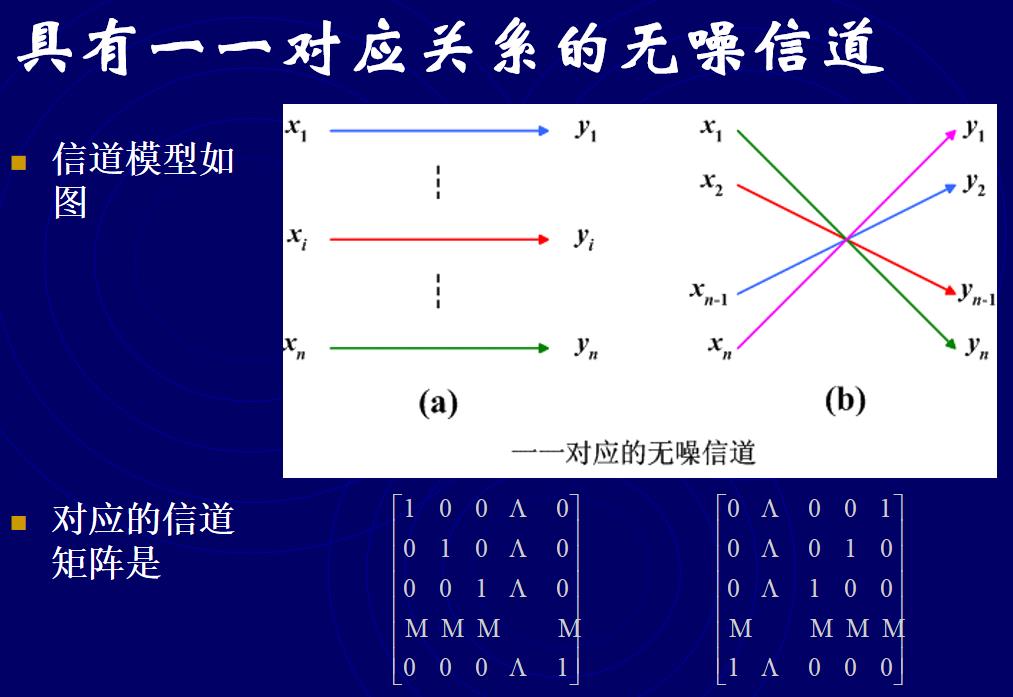
这个图中的A和M符号都表示省略号。
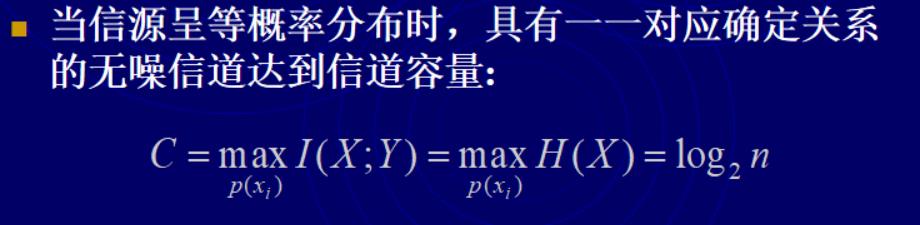
3.1.2具有扩展性能的无噪信道
这种信道的特点是输入X的符号集个数小于输出Y的符号集个数,即n<m。信道矩阵中的元素不全是0或1,每列中只有一个非零元素。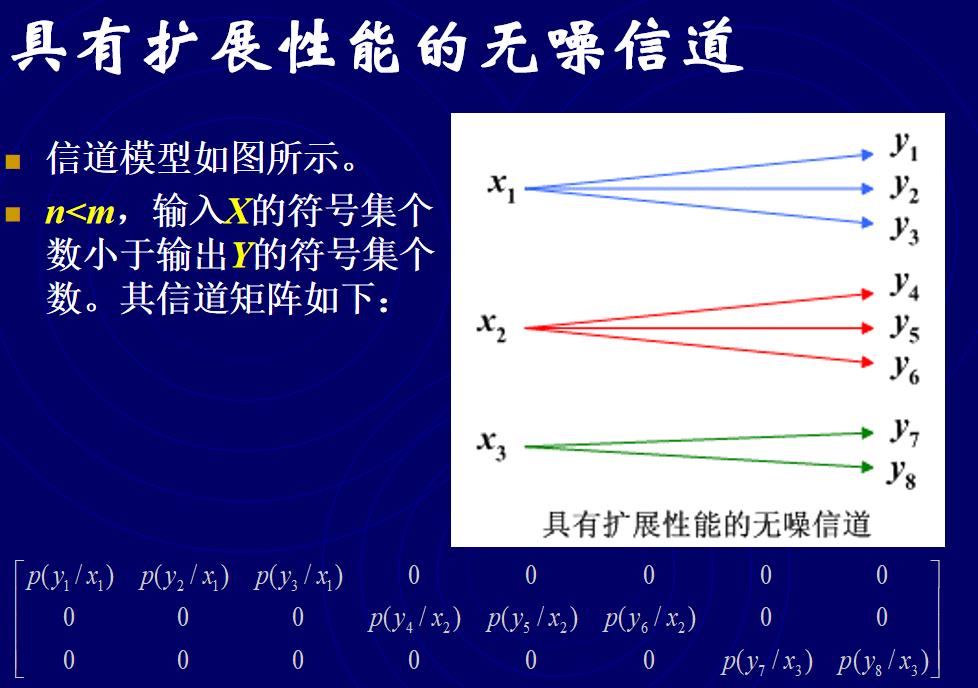
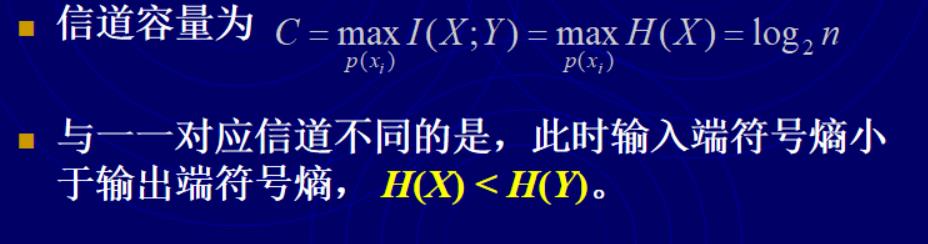
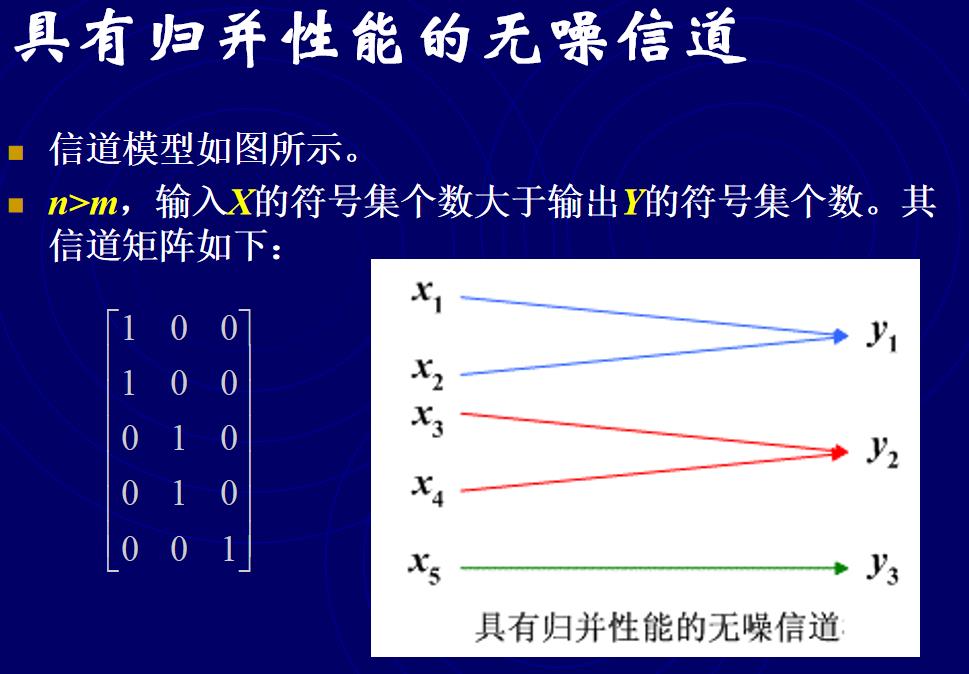
3.1.3具有归并性能的无噪信道
这种信道的特点是信道矩阵中的元素非0即1,每行仅有一个非零元素,但每列的非零元素个数大于1。
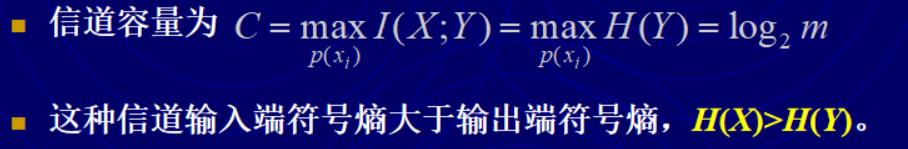
3.2强对称离散信道的信道容量


四、多符号离散信道的信道容量
4.1离散无记忆扩展信道的信道容量
结论1:离散无记忆信道的N次扩展信道的平均互信息,不大于N个随机变量X1X2…XN单独通过信道{X P(Y/X) Y}的平均互信息之和。即: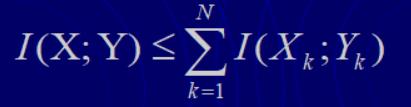
结论2:离散无记忆信道的N次扩展信道,当输入端的N个输入随机变量统计独立时,信道的总平均互信息等于这N个变量单独通过信道的平均互信息之和。
结论3:离散无记忆信道的N次扩展信道,如果信源也是离散无记忆信源的N次扩展信源,则 信道总的平均互信息是单符号离散无记忆信道平均互信息的N倍。
用C表示离散无记忆信道容量,用CN表示其扩展信道容量,CN=NC。
总结
第四章内容与第二章类似,且有许多交叉,比如自信息与互信息,两章结合起来看,多做题加深理解:)
以上是关于《信息与编码》考试复习笔记4----第四章离散信道容量的主要内容,如果未能解决你的问题,请参考以下文章
《信息与编码》考试复习笔记6----第六章连续信源熵和信道容量(考点在连续信道容量)
《信息与编码》考试复习笔记6----第六章连续信源熵和信道容量相关例题
《信息与编码》考试复习笔记3----第三章无失真离散信源编码(重要)