区块链：3共识算法 拜占庭将军问题

Posted 2021-06-02 DonquixoteXXXXX

区块链：3、共识算法 拜占庭将军问题

区块链系统采用分布式共识算法在无中心节点控制，又可能存在破坏节点的环境下确立系统状态，从而建立信任。区块链因此也被称为信任机器。

共识算法因不同的应用场景而有所不同。
从区块链的部署架构来看，有适合于公有链的共识算法，也有适合于联盟链或私有链的共识算法。公有链上的共识算法一般需要支持高扩展性，能够在共识节点动态出入网络的情况下保证共识流程的节奏，同时又要防止拜占庭节点对网络的攻击。

不同的共识算法在一致性、 正确性、可终止性、交易吞吐量、记账频率、扩展性和安全性上各有不同。在实际应用中，需要根据应用场景，选择能满足应用需求的共识算法。

分布式共识算法是分布式系统中保证系统状态一致性的重要技术，是分布式文件系统、分布式数据库的重要基础。

两阶段提交(Two-PhaseCommit)

在数据库系统中，两阶段提交(Two-PhaseCommit)是一个普遍使用的保证一致性的方法。两阶段提交由一个协调节点(Coordinator)居中控制。

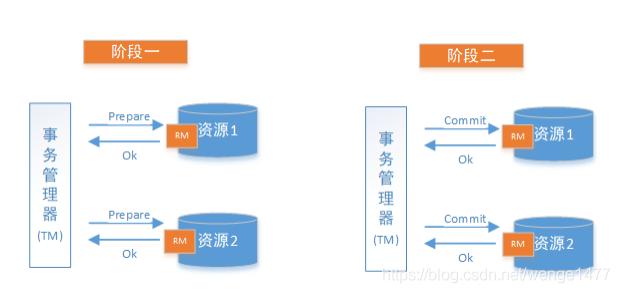
第一阶段：协调节点会向所有节点发送一个询问“是否准备好”的消息，各节点会响应该消息。

第二阶段：如果各节点的响应都是准备好的回复，协调节点会向各节点发“提交"指令，否则会发“回滚”指令。

这样所有节点的状态都会保持一致, 要么提交新的状态，要么回滚成以前的状态。
两阶段提交协议在没有出现节点故障的情况下可以保证系统状态的一致性，但是当协调节点和另外一个节点同时出故障的时候，系统没有办法知道故障节点的状态，因此无法决定是提交还是回滚。

三阶段提交(Three-Phase Commit)

为了解决这个问题，三阶段提交(Three-Phase Commit)协议被提出来：

即在正式提交前，协调节点再发一次“准备提交”的消息，在收到所有节点的回复后，协调节点才发“提交”的指令。
三阶段提交能部分解决两阶段提交中协调节点和另一节点同时出故障的问题，但是系统过分依赖一个协调节点，另外其余节点也没有办法形成对协调节点是否出现故障的共识，因此，无论两阶段提交还是三阶段提交,都不能作为一个分布式共识算法，只能在通常情况下保障分布式系统的一致性。

两阶段提交和三阶段提交多数用在同步通信的分布式系统中，而通常的分布式系统是由多个主机通过吊少通信方式组成网络集群。在这样的一个异步系统中,需要主机之间进行状态复制，以保证每个主机达成一致的状态共识。 然而，异步系统中可能出现无法通信的故障主机，而主机的性能可能下降、网络可能拥塞，这些可能导致错误信息在系统内传播。因此需要在默认不可靠的异步网络中建立容错协议,以确保各主机达成安全可靠的状态共识。

利用区块链构造基于互联网的去中心化账本，需要解决的首要问题是如何实现不同账本节点上账个数据的一致性和正确性。这就需要借鉴已有的、在分布式系统中实现状态共识的算法，确定网络中选择记账节点的机制，以及如何保障账本数据在全网中形成正确、一致的共识。

在20世纪80年代出现的分布式系统共识算法，是区块链共识算法的基础。

一、拜占庭将军问题 .

拜占庭将军问题是区块链平台的共识机制需要解决的一个核心问题。

1、问题提出与约束条件

拜占庭将军问题是Leslie Lamport在20世纪80年代提出的一个假象问题。拜占庭是东罗马帝国的首都，由于当时拜占庭罗马帝国国土辽阔，每支军队的驻地分隔很远，将军们只能靠信使传递消息。发生战争时，将军们必须制订统一的行动计划。然而，这些将军中有叛徒。叛徒希望通过发布错误消息来影响忠诚的将军们制定统一的行动计划，以达到破坏忠诚的将军们统一行动的目的。因此，将军们必须有一个预定的方法协议，满足两个条件:

 1、使所有忠诚的将军能够达成一致;
 2、少数几个叛徒不能使忠诚的将军做出错误的计划。

条件2比较难用形式化方式描述，这里需要了解的是将军们怎么做决策。一般来说，每个将军会把他观察到的敌情派通信员告知其他将军。假设v(i)是第i个将军通知其他将军的消息，每个将军会采用某种方法把所有收到的消息v(1)…v(n)组成一个单一的行动计划，其中n是将军的数目。

条件1可以通过采用同一方法组成行动计划来达到
条件2则可以通过某种鲁棒性方式来达到，例如，通过多数人的意见来决定最后的行动计划。

如果要满足条件1，下列条件必须满足:
(1)每个忠诚的将军必须收到相同的命令值v(1)...v(n)。(v(i)是第i个将军的命令);					
(2)如果第i个将军是忠诚的，那么他发送的命令和每个忠诚将军收到的v(i)相同。

Lamport把以上所有将军互相发命令的问题简化成一个将军发指令给n-1个副官，从而得出拜占庭将军问题。

拜占庭将军问题——一个发送命令的指挥官要发一个命令给其余n-1个副官，使得:

C1:所有忠诚的接收命令的副官遵守相同的命令;
C2: 如果发送命令的指挥官是忠诚的,那么所有忠诚的接收命令的副官将遵守所接收的命令。

拜占庭将军论断

Lamport指出在将军通过通信员口头传递信息的情况下，只要有1/3以上的叛徒，则没法保证忠诚的副官能达成一致的行动。

Lamport采用一个简单的图来说明在一个指挥官两个副官的情况下，只要有一个叛徒存在，就不可能达成共识。当指挥官是叛徒的情况下，忠诚的副官1和副官2没法遵从同样的命令，因此没办法保障C1的成立。

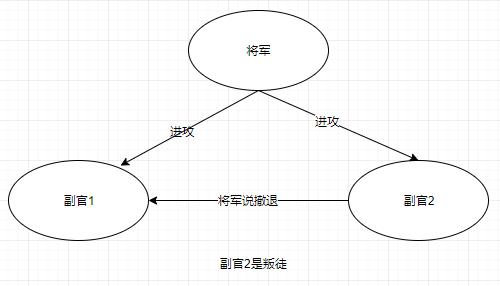
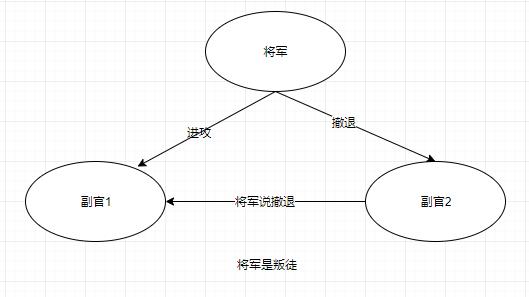
Lamport对拜占庭将军问题的研究表明，当n>3m时，即叛徒的个数m小于将军总数n的1/3时，通过口头同步通信(假设通信是可靠的)，可以构造同时满足C1和C2的解决方案，即将军们可以达成一致的命令。
但如果通信是可认证、防篡改伪造的(如采用PKI认证，消息签名等)，则在任意多的叛徒(至少得有两个忠诚将军)的情况下都可以找到解决方案。

Lamport对口头同步通信的定义如下:
A1.每个发送的消息都会被正确接收;
A2.接收消息的人知道是谁发送的消息;
A3.消息没有发送可以被检测到。

Lamport利用递归的方式定义了一个能在系统中叛徒少于1/3的将军总数的情况用口头同步信息达成共识的算法，简单表示成OM (m),即在最多m个叛徒的情况下，采算法能使总共超过3m+1的将军解决拜占庭将军的问题。该算法假设有一个majority函数，当大多数的vi值等于v，则maijority(vI，…，vn-1)等于v。如果vi不存在,该函数值是RETREAT (撤退是缺省值)。

2、算法与定理

（1）算法OM(0)(m=0,没有叛徒的情况)

①指挥官发他的值(相当于命令)给每一个副官。

②每个副官用他接收到指挥官的值作为当前值，如果没有接收到，用RETREAT (缺省是撤退)。

（2）算法OM (m), m>0

①将军发他的值给每一个副官。

②对每个i,让vi等于副官i从指挥官那里接收到的命令,或者如果没有接收到指令的话值就是RETREAT (缺省撤退)。副官i作为算法0M(m-1)的将军，发vi给其他n-2个副官。

③对每个i,以及每个j≠i,让vj等于第2步中采用算法0M(m-1)副官i从副官j接收到的值，或者没有收到值则缺省为RETREAT。副官i取majority(v1, … vn-1)的值。

为了证明算法OM(m)对任意m都能解决拜占庭将军问题，要先证明以下引理:

引理1:对任意m和k,如果有多于2k+m个将军和最多k个叛徒，算法OM (m)满足C2。

证明采用归纳法。
C2 只是规定在指挥官是忠诚的情况下需要满足的条件。
根据A1，可以很容易看出当指挥官是忠诚的时候，OM (0)成立，所以引理1在m=0的情况下成立。
我们现在假设在m-1, m>0的情况下成立，
我们只需要证明m情况下也成立，通过数学归纳法，我们可以得出引理1成立。
在算法OM(m)第一步，忠诚的指挥官发一个值v给所有n-1个副官。
在第二步，每个忠诚的副官递归调用0M (m-1),总共n-1个将军。
根据假设n>2k+m，我们可以得到n-1>2k+(m-1), 
所以我们可以采用归纳法来得出每个忠诚的副官从第j个忠诚的副官处得到vj=v。
因为最多只有k个叛徒，并且n-1>2k+(m-1)>2k,所以n-1个副官中的多数是忠诚的。
因此，每个忠诚的副官都在n-1个副官的多数中收到vi=y,
所以他在第三步会得到majort(1,,n-1)=v,证明了C2,
即当指挥官是忠诚的情况下，所有忠诚的副官都执行接收的命令。

以下定理确认算法OM(m)能解决拜占庭将军问题。

定理1:对任意m,如果在至多m个叛徒而将军数超过3m个的情况下，算法OM (m)满足条件C1和C2。

采用归纳法来证明。
如果没有叛徒，很容易得出OM(0)满足C1和C2。
我们假设定理在OM (m-1)时成立，然后我们只需要证明在 OM (m), m>0时也成立。.

首先我们考虑将军是忠诚的情况。
在引理1中，使r=m，我们可以得出OM(m)满足C2。
如果将军是忠诚的，C1也会自动满足。
所以我们只需要在将军是叛徒的情况下验证C1。
最多只有m个叛徒，由于指挥官是其中一个，因此有m-1个副官是叛徒。
因为有超过m个将军，会有超过3m-1个副官，而且3m-1>3(m-1).
我们因此采用递归法来得出OM(m-1)满足条件C1和C2。
所以,对每个j，任何两个忠诚的副官在第三步的时候即会得到相同的vi.
(如果两个副官中的一个是副官j， 可以从C2中得出，否则可以从C1中得出）
因此，任意两个忠诚的副官都可以得到一样的向量v1,...,vn-1
因此会在第三步在一样的majority(v1,...vn-1),证明Cl成立。

3、拜占庭将军问题实质

综上所述，拜占庭将军问题的实质就是要寻找一个方法，使得在有故障得情况下能建立系统的共识。

在分布式系统中，特别是在区块链网络中的环境也和拜占庭将军的环境类似，有运行正常的服务器，有存在故障的服务器， 还有破坏者的服务器（类似叛变的拜占庭将军）。

共识算法的核心是在正常的节点间形成对网络状态的共识，也就是解决拜占庭将军问题。

二、 共识系统的基本定义

拜占庭将军问题在一个分布式系统中是一个非常有挑战的问题。

先给出分布式计算中有关拜占庭缺陷和故障的4个定义。

拜占庭缺陷： 任何从不同观察者角度看表现出不同症状的缺陷。

拜占庭故障：在需要共识的系统中由于拜占庭缺陷导致丧失系统服务。

宕机缺陷：在需要共识的系统中导致进程停止运行发生的缺陷;该缺陷不对系统产生其他副作用。

宕机恢复故障： 在需要共识的系统中导致进程停止运行发生的故障:该故障在重启进程后恢复，不对系统产生其他副作用。

在分布式系统中，不是所有的缺陷或障都能称为拜占庭缺陷或故障。像宕机、丟消息等缺陷或故障不能算作拜占庭缺陷或故障。
拜占庭缺陷或故障是最严重缺陷或故障。拜占庭缺陷有不可预测、任意性的特点，例如遭黑客破坏、中木马的服务器就是一个拜占庭服务器的例子。

在一个分布式系统中，所有的进程都有一个初始值。在这种情况下，共识问题就是要寻找一个算法和协议,使得该协议满足以下三个属性:

1 )一致性(Agreement):所有的非缺陷进程都必须同意同一个值。

2)正确性(Validity):所有非缺陷的进程所同意的值必须来自非故障进程所提议的值。

3)可结束性(Termination): 每个非缺陷的进程必须最终确定一个值 。

通常也把满足一致性和正确性称为安全性(Safety)，而满足可结束性称为活性(Liveness)。

在异步通信的分布式系统中,只要有一个拜占庭缺陷的进程，就不可能找到一个共识算法可同时满足上述要求的一致性、正确性和可结束性，也就是说，不能同时满足安全性和活性。

在实际情况下，根据不同的假设条件，有很多不同的共识算法被设计出来，这些算法各有优势和局限。算法的假设条件有以下几种情况。

1)故障模型:非拜占庭故障/拜占庭故障。

2)通信类型:同步/异步。

3)通信网络连接:节点间直连数。

4)信息发送者身份:实名/匿名。

5)通信通道稳定性:通道可靠/不可靠。

6)消息认证性:认证消息/非认证消息。

通常使用的共识算法，如果按照严格的FLP异步通信的假设,往往只满足安全性而牺牲活性。

也就是说，大部分使用的异步通信网络下的共识算法,往往不能保证在有限的时间内总能达成共识。

参考文献

[1]邹均.于斌.庄鹏.邢春晓.区块链核心技术与应用.机械工业出版社