向量总结

Posted 2021-06-02 月疯

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了向量总结相关的知识，希望对你有一定的参考价值。

既有大小又有方向的量叫做向量。

1、向量积可以被定义为：

模长：（在这里θ表示两向量之间的夹角(共起点的前提下)（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。）

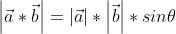
$\\left | \\vec{a}*\\vec{b} \\right |=\\left | \\vec{a} \\right |*\\left | \\vec{b} \\right |*sin\\theta$

2、向量的大小，也就是向量的长度(或称模)。

空间向量（x，y，z），其中x，y，z分别是三轴上的坐标，模长是

$\\sqrt[2]{x^{2}+y^{2}+z^{2}}$

平面向量（x，y），模长是：

$\\sqrt[2]{x^{2}+y^{2}}$

3、向量的和的模

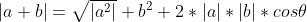
$\\left | a+b \\right |=\\sqrt{\\left |a ^{2} \\right |}+b^{2}+2*\\left | a \\right |*\\left | b \\right |*cos\\theta$

4、数量积

数量积（又叫内积、点积）

向量的内积（点乘）

俩个向量a与b的内积为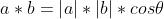 $a*b=\\left | a \\right |*\\left | b \\right |*cos\\theta$ ,特别地，0·a =a·0 = 0；若a，b是非零向量，则a与b****正交的充要条件是a·b = 0。

向量内积的几何意义

内积（点乘）的几何意义包括：

向量的外积（叉乘）

a=(x1,y1,z1)

b=(x2,y2,z2)

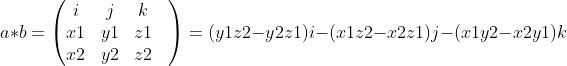
$a*b=\\begin{pmatrix} i & j& k& \\\\ x1& y1& z1&\\\\ x2 & y2 & z2&\\\\ \\end{pmatrix}=(y1z2-y2z1)i-(x1z2-x2z1)j-(x1y2-x2y1)k$

其中，i=(1,0,0);j=(0,1,0);z=(0,0,1)

关系：

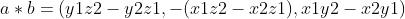
a*b=(y1z2-y2z1,-(x1z2-x2z1),x1y2-x2y1)

以上是关于向量总结的主要内容，如果未能解决你的问题，请参考以下文章