有意思的希尔排序

Posted 2021-06-02 代码两三事

希尔排序的称呼蛮多的，什么“递减增量排序算法”，什么“缩小增量排序算法”，其实希尔排序本质上算是一个分组插入排序算法，可以称之为插入排序的plus版本。查询百度百科可以知道算法是1959年提出，作者D.L.Shell。

算法操作

希尔排序算法操作起来是这样的：

1. 首先计算一个增量值

2. 按增量将集合分组，每一组数据使用插入排序算法排序

3. 增量-1，继续步骤2；直到增量值减少为1进行最后一次插入排序后，算法结束。

希尔排序是个分组插入排序算法，这里的“增量”其实就是用于数据跳跃式分组的数据元素间隔、“步长”、数据元素缝隙个数。一般情况下增量值的取值是数据集合中元素的个数size/2（一般都是除以2向下取整得出结果），以后每趟减半，直到增量值为1。

例如有如下一个数组：

图1

1. 第一趟，数组长度10，按公式计算第一趟时的增量或者说“步长”，值为10/2=5。按增量值5对数据进行分组，结果如图2

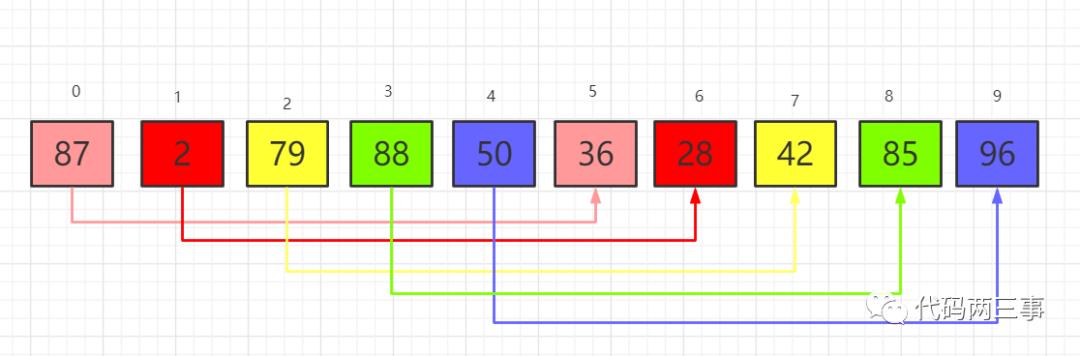
图2

第一组：87,36；第二组：2,28；第三组：79,42；第四组：88,85；第五组：50,96。

按上面提到的步骤2，每组进行插入排序。第一组87大于36，36插入到87前面。第二组2小于28，顺序不变。后续几组以此类推。调整后的结果为：

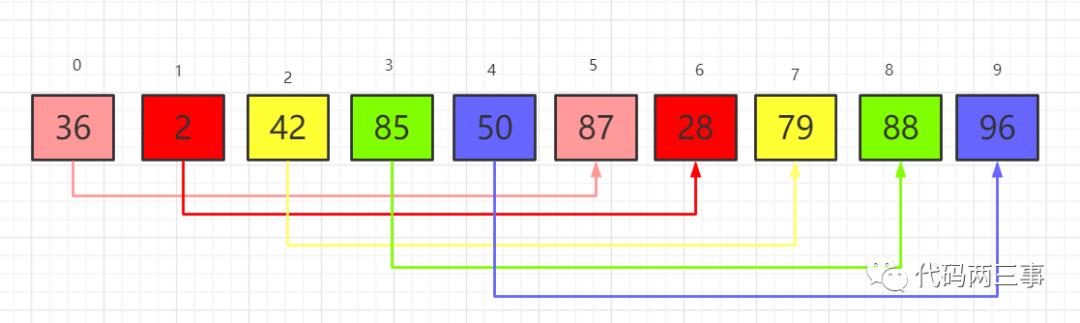
图3

2. 第二趟，增量减半，5/2=2（向下取整）。按增量为2进行分组。如图：

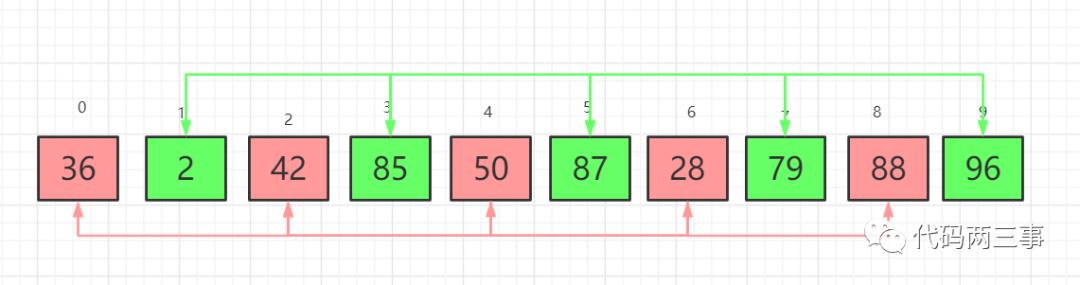
图4

第一组：36,42,50,28,88；第二组：2,85,87,79,96。每组组内进行插入排序后结果如下：

图5

3. 第三趟，增量减半，2/2=1。当增量为1时，直接转化为简单插入排序。简单插入排序细节参考。

代码实现

首先，计算增量长度，并且持续进行减半操作，直到增量值为1。这个比较简单，一个for循环轻松搞定。

    public static void shellSort(int[] array) {
        if (null == array || array.length < 2) return;
        //计算增量值，每趟减半，直到为1
        for (int gap = array.length / 2; gap >= 1; gap = gap / 2) {

        }
    }

第二，考虑到每次分组组内都是插入排序，只不过有个gap增量值在里面。另外一个简单插入排序算法中其实也是有增量值存在的，只不过增量值为1。

我们只要把上图算法中的1全部用gap代替即可。

所以希尔排序算法的代码实现即为：

public static void shellSort(int[] array) {
    if (null == array || array.length < 2) return;
    //计算增量值，每趟减半，直到为1
    for (int gap = array.length / 2; gap >= 1; gap = gap / 2) {
        //默认第一个元素是已排序元素，所以i直接从下标为gap的item开始
        for (int i = gap; i < array.length; i = i + gap) {
            int temp = array[i];//在待排序集合中选择第一个元素为新元素
            int j = i - gap; //找到已排序元素的末尾
            //从已排序集合的末尾开始向前扫描，只要元素大于新元素，就向后挪动gap位
            while (j >= 0 && array[j] > temp) {
                array[j + gap] = array[j];//向后挪动gap位
                j = j - gap;//指向已排序元素的指针减减，向左挪动gap位
            }
            //此时j+gap的空位就是新元素在已排序集合中合适的位置。插入即可
            array[j + gap] = temp;
        }
    }
}

算法分析

时间复杂度

希尔排序的时间复杂度比较复杂，依赖于增量数组的选择。

具体的最好时间复杂度，最坏复杂度，平均复杂度很多资料里记录的都不一样。这里暂时记录一下一些比较明确的结论：1）希尔排序比简单插入排序算法的O(n^2)要快，但是面对大规模的数据时比快速排序这样的O(nlogn)速度又要慢。2）和简单插入排序算法一样，如果是一个已经排序好的数组，最好时间复杂度是O(n)。

空间复杂度

希尔排序内部排序使用的是简单插入排序，因此空间复杂度是常数阶O(1)。

稳定性

虽然简单插入排序算法是一个稳定的排序算法，但是希尔排序算法不是稳定的排序算法。原因在于希尔排序跳跃式的分组，很容易改变相同值的相对位置。

关于希尔排序的一点思考

希尔排序之所以能突破简单排序排序算法的O（n^2）的时间，在于它利用简单插入排序算法的优点时，修正了它的缺点。

先说优点，简单插入排序算法相比于其他排序算法有一个非常突出的优点——可以提前终止。即在一个有序的数组中，如果发现元素item已经插入到该item合适的位置，就会停止不会往前继续比较。数组越是有序，这种特性就发挥的越好，因此它最好情况下可以得到O（n）的线性排序时间。

接着说说缺点。使用简单插入排序时如果最小值在末尾，就需要从尾部开始往前挨个比较大小，一直找到队头位置，然后插入最小值，非常低效。如果这个时候数据量再大一点，那乐子就更大了。

希尔排序通过设置增量值跳跃式的对数据进行分组，可以让头部和尾部的数据直接进行比较，解决了简单插入排序的这个缺陷。再利用简单插入排序算法在有序数组中特别高效这一特性，两项叠加由此突破了算法复杂度O(n^2)的限制。