变分自编码器的原理与项目实战

Posted 2021-06-02 Charmve

本文来自于GitHub《计算机视觉实战演练：算法与应用》，全书请参考原文。

链接：https://github.com/Charmve/computer-vision-in-action

第 12 章 生成对抗模型

作者: 张伟 (Charmve)

日期: 2021/05/19

• 第 12 章 生成对抗模型
  • 12.1 Pixel RNN/CNN
  • 12.2 自编码器 Auto-encoder
  • 12.3 生成对抗网络 GAN
    • 12.3.1 原理
    • 12.3.2 项目实战
      • StyleGAN
      • StyleGAN 2.0
  • 12.4 变分自编码器 Variational Auto-encoder, VAE
  • 参考文献

---

12.4 变分自编码器 Variational Auto-encoder, VAE

• 12.4.1 概述
• 12.4.2 基本原理
  • 2.1 Encoder
  • 2.2 Decoder
  • 2.3 Self-Attention
  • 2.4 Multi-Headed Attention
  • 2.5 Positional Encoding
• 12.4.3 应用任务和结果
  • 3.1 NLP领域
  • 3.2 CV领域
    • 3.2.1 检测DETR
    • 3.2.2 分类ViT
    • 3.2.3 分割SETR
    • 3.2.4 Deformable-DETR
• 12.4.4 优点及分析
• 12.4.5 缺点及分析
• 参考文献

12.4.1 概述

VAE 模型是一种有趣的生成模型，与GAN相比，VAE 有更加完备的数学理论（引入了隐变量），理论推导更加显性，训练相对来说更加容易。

VAE 可以从神经网络的角度或者概率图模型的角度来解释。

理解变分自编码器的基本原理只需要关注整个模型的三个关键元素：

• 编码网络（Encoder Network），也称 推断网络 。该 NN 用来生成隐变量的参数（隐变量由多个高斯分布组成）。对于隐变量 $z$ ，首先初始化时可以是标准高斯分布，然后通过这个 NN，通过不断计算后验概率 $q(z|x)$ 来逐步确定高斯分布的参数（均值和方差）。
• 隐变量(Latent Variable)。作为 Encoder 过程的产物，隐变量至少能够包含一些输入数据的信息（降维的作用），同时也应该具有生成类似数据的潜力。
• 解码网络(Decoder Network)，也称 生成网络。该 NN 用于根据隐变量生成数据，我们希望它既有能力还原 encoder 的数据，同时还能根据数据特征生成一些输入样本中不包含的数据。

本文来自于GitHub《计算机视觉实战演练：算法与应用》，全书请参考原文。

链接：https://github.com/Charmve/computer-vision-in-action

12.4.2 基本原理

1. 定义

VAE 全名叫 变分自编码器，是从之前的 auto-encoder 演变过来的，auto-encoder 也就是自编码器，自编码器，顾名思义，就是可以自己对自己进行编码，重构。所以 AE 模型一般都由两部分的网络构成，一部分称为 encoder, 从一个高维的输入映射到一个低维的隐变量上，另外一部分称为 decoder, 从低维的隐变量再映射回高维的输入：

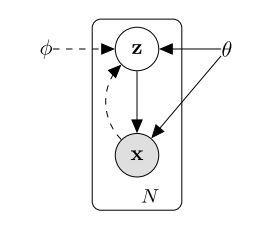
(a) VAE模型

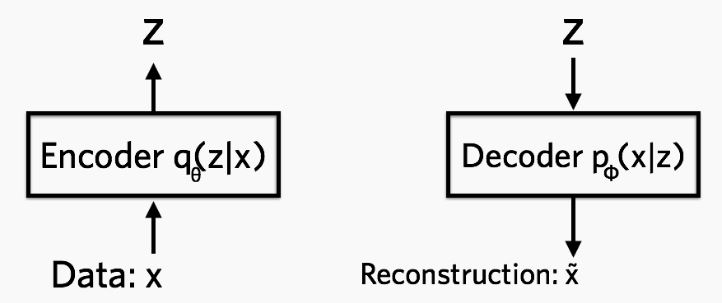
(b) 编码与重构

图1 VAE模型

如上图所示，我们能观测到的数据是 $x$ ，而 $x$ 由隐变量 $z$ 产生，由 $z->x$ 是生成模型 $p_{\varphi }(x|z)$ ，从自编码器（auto-encoder）的角度来看，就是 解码器 decoder；而由 $x->z$ 是识别模型（recognition model）$ q_{\\theta}(z|x)$ ，类似于自编码器的 编码器 encoder。

简单而言，encoder 网络中的参数为 $\theta$, decoder 中网络中的参数为$\varphi$， $\theta$ 就是让网络从 $x$ 到 $z$ 的映射，而 $\varphi$ 可以让网络完成从 $z$ 到 $x$ 的重构。可以构造如下的损失函数：

$$l_i(\theta ,\varphi )=-E_{z\sim q_{\theta }(z|x_i)}[log(p_{\varphi }(x_i|z))]+KL(q_{\theta }(z|x_i)||p(z))$$

式（1）

上面的第一部分，可以看做是重建 loss，就是从 $x\sim z\sim x$ 的这样一个过程，可以表示成上面的熵的形式，也可以表示成最小二乘的形式，这个取决于 $x$ 本身的分布。后面的 KL 可以看做是正则项，$q_{\theta }(z|x)$ 可以看成是根据 $x$ 推导出来的 $z$ 的一个后验分布，$p(z)$ 可以看成是 $z$ 的一个先验分布，我们希望这两个的分布尽可能的拟合，所以这一点是 VAE 与 GAN 的最大不同之处，VAE对隐变量 $z$ 是有一个假设的，而 GAN 里面并没有这种假设。 一般来说，$p(z)$ 都假设是均值为0，方差为1的高斯分布 $\mathcal{N}(0,1)$。

如果没有 KL 项，那 VAE 就退化成一个普通的 AE 模型，无法做生成，VAE 中的隐变量是一个分布，或者说近似高斯的分布，通过对这个概率分布采样，然后再通过 decoder 网络，VAE 可以生成不同的数据，这样VAE模型也可以被称为生成模型。

<你可能会问> 为什么叫变分自编码器？

推荐了解一下 变分推断，这里摘取其中某位大牛的回答：“简单易懂的理解变分其实就是一句话：用简单的分布q去近似复杂的分布p。”
所以暂时如果不考虑其他内容，联系一下整个 VAE 结构，应该就能懂变分过程具体是指什么了。 VAE 中的隐变量 $z$ 的生成过程就是一个变分过程，我们希望用简单的 $z$ 来映射复杂的分布，这既是一个降维的过程，同时也是一个变分推断的过程。

2. 理论基础：三要素

该部分推导主要参考李宏毅老师的 课件视频

Step 1 - 引入隐变量 z

隐变量(Latent Variable)。上面已经讲过隐变量的基本概念，这里介绍隐变量在 VAE模型中的作用及特点。

• 隐变量 $z$ 是可以认为是隐藏层数据，它是不限定数目的符合 高斯分布 特征的数据。（根据实际情况确定数目）
• $z$ 由输入数据 X XX 的采样以及参数生成，它既包含 $X$ 的信息（这个于 AutoEncoder 的隐藏层类似），同时也满足 高斯分布，方便接下来进行梯度下降或者其他优化技术 [1]。
• 隐变量的作用除了让生成网络尽可能还原原来的数据 $X$ ，同时也能生成原来数据中不存在的数据。

首先当我们引入隐变量 $z$ 以后，可以用 $z$ 来表示 $P(x)$ ：

$$P(X)={\int }_{z}P(X|z)P(z)\mathrm{d}z(1)$$

其中，用 $P(X|z)$ 替代了 $f(z)$ ，这样可以用概率公式明确表示 X 对 Z 的依赖性；$P(z)$ 即高斯分布；其中 $X|z $ ~ $\mu N((z),\sigma (z))$，其中的均值 $\mu (z)$ 和 方差 $\sigma (z)$ 需要通过运算获得。

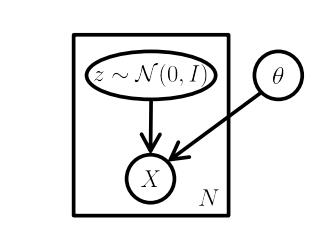
图2 VAE模型的一个图模型

如图所示，标准的VAE模型是一个图模型，注意明显缺乏任何结构，甚至没有 “编码器” 路径：可以在不输入的情况下从模型中采样。这里，矩形是 “板符号”，这意味着我们可以在模型参数 $\theta$ 保持不变的情况下，从 $z$ 和 $X$ 中采样N次。

Step 2 - Decoder 过程

上面也曾讲过，VAE 模型中同样有 Encoder 与 Decoder 过程，也就是说模型对于相同的输入时，也应该有尽可能相同的输出。所以这里再次遇到 Maximum likelihood（极大似然）。

在公式 (1) 中，将 $P(X)$ 用 $Z$ 来表示，所以对任何输入数据，应该尽量保证最后由隐变量而转换回输出数据与输入数据尽可能相等。

$$L=\sum _{x}logP(X)$$

式（2）

为了让公式 2 的输出极大似然 $X$ ，神经网络登场，它的作用就是调参，来达到极大似然的目的。（注意这里虽然介绍在前，但其实在训练的时候与后面的 NN 是同时开始训练）

本步介绍的是如何实现与 AE 类似的功能，即保证输出数据极大似然与输入数据。

这里用到的网络称为 VAE 中的 生成网络，即根据隐变量 $Z$ 生成输出数据的网络。

Step 3 - Encoder 过程

这个步骤需要确定隐变量 $Z$ ，也就是 Encoder 过程。

这里需要用到另外一个分布，$q(z|x)$ ，其中 $q(z|x)$ ~ $N({\mu }^{\prime }(x),{\sigma }^{\prime }(x)$ ，注意这里的均值和方差都是对 $X$ 进行的。

同样地，这个任务也交给 NN 去完成。

这里的网络称为 推断网络。

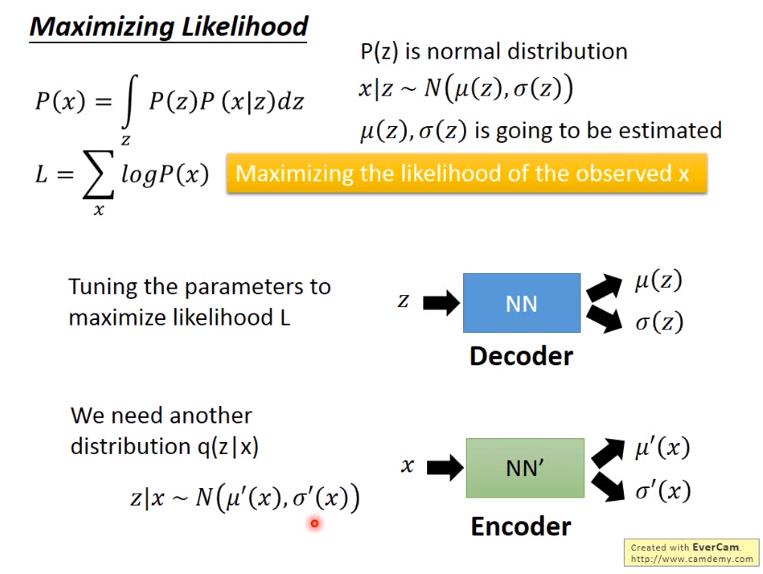
图3 最大似然估计

Step 4 ELBO

这里对 $logP(X)$ 进行变形转换。
$$\log P(X)={\int }_{z}q(z|x)\log P(x)\mathrm{d}z$$

式（3）

在公式3中， $q(z|x)$ 可以是任意分布。

为了让 Encode 过程也参与进来，这里引入 $q(z|x)$，推导步骤如下：

log ⁡ P ( X ) = ∫ z q ( z ∣ x ) log ⁡ P ( x )   d z                          = ∫ z q ( z ∣ x ) log ⁡ ( P ( z , x ) P ( z ∣ x ) )   d z                                      = ∫ z q ( z ∣ x ) log ⁡ ( P ( z , x ) q ( z ∣ x ) q ( z ∣ x ) P ( z ∣ x ) )   d z                 

以上是关于变分自编码器的原理与项目实战的主要内容，如果未能解决你的问题，请参考以下文章

一文搞懂变分自编码器(VAE, CVAE)

变分自编码器（Variational Autoencoder, VAE）通俗教程

VAE 变分自编码器

VAE 变分自编码器

VAE 变分自编码器

机器学习-白板推导系列(三十二)-变分自编码器(VAE，Variational AutoEncoder)