2021-05-28

Posted 2021-06-02 xiao zhou

二叉树常见操作及OJ练习

• 写在前面（很重要）
• 一、二叉树常见操作
• • 1.深度优先遍历（前、中、后序）
  • 2.求整棵树中结点个数
  • 3.求叶子结点的个数
  • 4.求第K层结点的个数
• 二叉树的OJ练习
• • 单值二叉树
  • • 题目描述
    • 问题分析：
    • 代码实现：
  • 2.二叉树的最大深度
  • • 题目描述
    • 问题分析：
    • 代码实现：

写在前面（很重要）

hehe在二叉树这里，我们经常要使用递归来解决问题，所以深刻理解递归解决问题的过程是极为重要的，在这里我不详细展开递归的介绍，我想先让你们深刻理解递归是如何将问题缩小，最终拆解成小问题并解决的。
hehe我们可以举这样例子来理解：一个学校要统计报名参加六级考试的人数，校长将任务分给院长，院长就要求自己院的人数，院长就把任务分给辅导员，辅导员就要求自己管理班级的人数，辅导员又把任务分配给班长，班长就很轻松的得到自己班级的人数，班长汇总给辅导员，辅导员汇总给院长，院长汇总给校长，校长得到最终的结果。
hehe在上级向下级分配任务的过程就是“递”的过程，在不断的拆解问题，而下级将任务结果返回给上级就是“归”的过程，从而得到最终的结果。
这是函数递归具体介绍和相关练习帮助理解的文章想看具体有关函数递归内容的老铁请点该链接
hehe还要再声明的一点就是，在代码的注释中，由书写代码要注意的问题，和在实现过程中仍然需要注意的小细节，所以要仔细阅读注释，才能真正理解所有题目是如何实现的

一、二叉树常见操作

首先先将树的结构体介绍一下

typedef struct BTNode	//树的结点的结构体
{
	BTDataType x;		//存该结点的值    //BTDdataType是指存储的数据类型
	struct BTNode* leftchild;	//储存左孩子的地址
	struct BTNode* rightchild;	//储存右孩子的地址

}BTNode;

1.深度优先遍历（前、中、后序）

（1）前序遍历：对于每一个结点，先访问该结点本身，再去访问它的左孩子，最后再去访问它的右孩子。

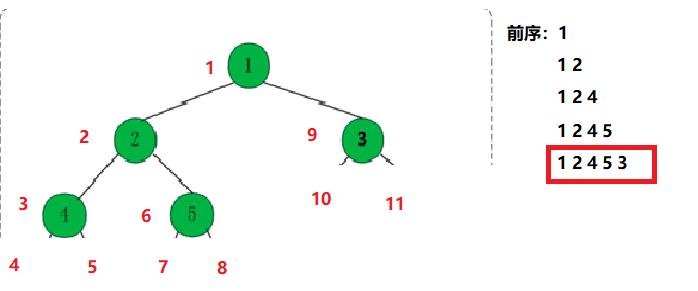
1：先访问本身1，再去访问1的左子树
2：先访问2本身，再去访问2的左子树4
3：先去访问4本身，再去访问4的左子树
4：4的左子树为空，所以返回至4
5：再去访问4的右子树，右子树为空，所以返回至4，此时4已经访问结束，返回至2，再去访问2的右子树
6：先访问5本身，再去访问5的左子树
7：左子树为空，返回至5
8：再去访问5的右子树，右子树为空，所以返回至5，此时5已经访问结束，所以返回至2，2也访问结束，所以返回至1
9：再去访问1的右子树3，先去访问3本身
10：再去访问3的左子树，左子树为空，返回至3，再去访问3的右子树
11：3的右子树为空，返回至3，3已经访问结束，返回至1，1访问结束，完成遍历
就是始终保证一个原则，就是遇到每一个结点先访问自己，再去访问它的左子树，然后再先访问左子树的根，再去访问左子树的根的左子树。。。无限套娃。当遇到空结点时时就返回，再去访问右子树，对于右子树也是先访问它的根，再去访问根的左子树。。。当一个结点右子树也遍历结束，那么这个结点就遍历结束。返回至它的双亲结点。当整棵树的根的右子树也遍历结束，说明整个树遍历结束。

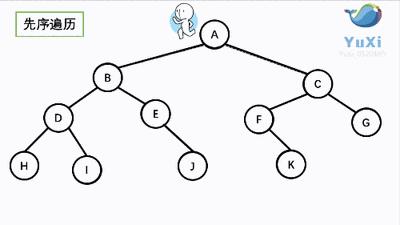```c void PrevOrder(BTNode* root) { if (root == NULL) //如果访问到空树，直接返回 { printf("NULL "); return; } printf("%c ", root->x); //先访问根自身 PrevOrder(root->leftchild);//再访问根的左子树（会不断递归，直到叶子节点） PrevOrder(root->rightchild);//再访问根的右子树（会不断递归，直到叶子节点） } ```

（2）中序遍历：对于每一个结点，先访问该结点的左子树，再访问该节点本身，最后访问该节点的右子树

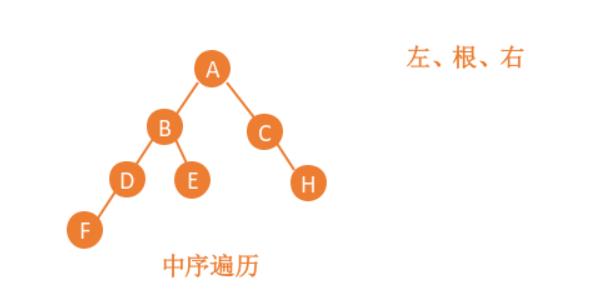
void InOrder(BTNode* root)
{
	if (root == NULL)	//访问到空树，直接返回
	{
		printf("NULL ");
		return;
	}
	InOrder(root->leftchild);//先去访问根的左子树（会不断递归，直到叶子结点）
	printf("%c ", root->x); //再访问根本身
	InOrder(root->rightchild);//最后访问根的右子树(会不断递归，直到叶子结点)
}

（3）后序遍历：对于每一个结点，先访问该结点的左子树，再访问该节点的右子树，最后访问该节点本身。

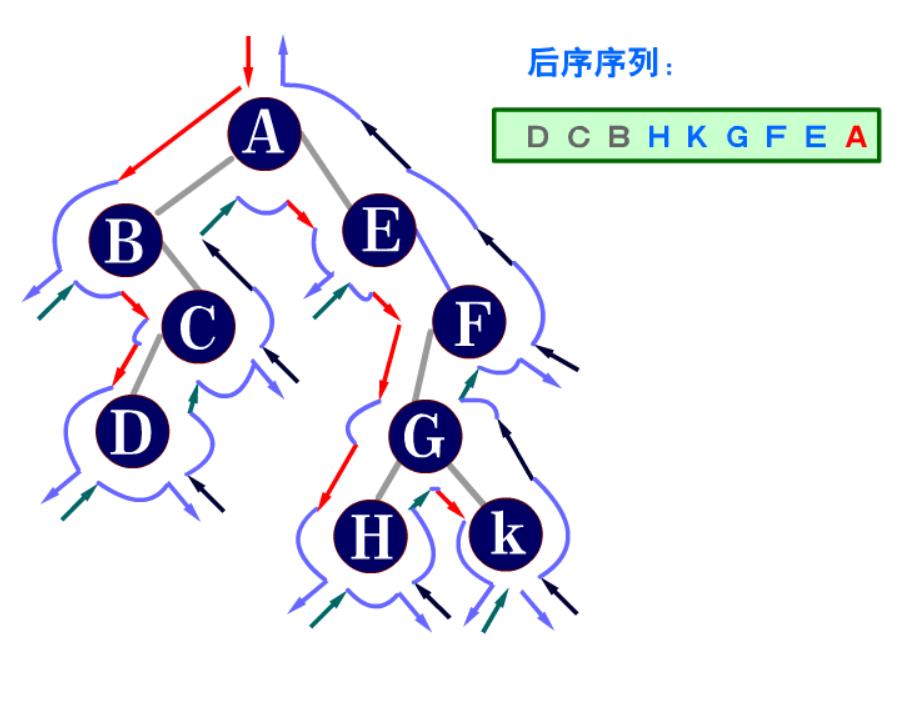
void PostOrder(BTNode* root)
{
	if (root == NULL)	//遇到空树直接返回
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->leftchild); //先访问根的左子树（直到叶子节点）
	PostOrder(root->rightchild); //再访问根的右子树（直到叶子节点）
	printf("%c ", root->x);		//最后访问根
}

2.求整棵树中结点个数

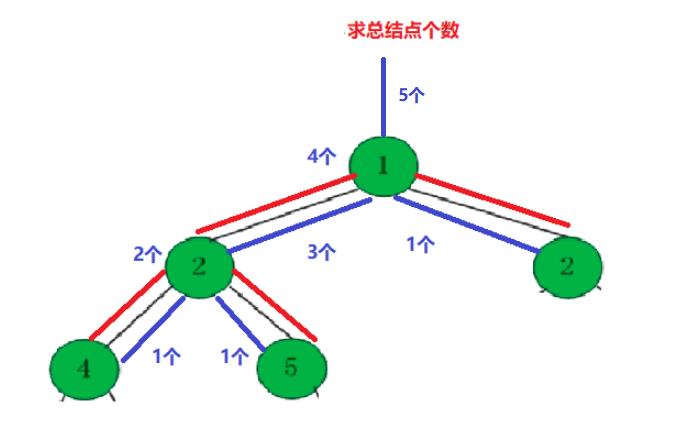
我们始终要牢记，在二叉树这里，我们能用递归就要使用递归，将大问题分解成一个一个小问题，简化问题，才能更加思路清晰的写代码实现相应功能。
而对于求结点个数的问题，我们可以拆解问题。
求：左子树的结点个数+右子树的结点个数+自身根

而左子树又可以分为：左子树的结点个数 = 左子树的左子树结点个数+左子树的右子树结点个数+左子树自身

右子树又可分为：右子树的结点个数 = 右子树的左子树结点个数+右子树的右子树结点个数+右子树自身

不断套娃套娃，就将问题分解成最后的叶子上。

int BTNodeSize(BTNode* root)
{
	//如果访问到空树，说明没有结点，那么值返回0
	if(root == NULL)	
		return 0；
	//不是空树，就计算左子树个数+右子树个数+自身的1个
	return BTNodeSize(root->left) + BTNodeSize(root->right) + 1;
}

3.求叶子结点的个数

叶子结点就是左右孩子都是空的结点。也是不断拆解问题
树的叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数

左子树的叶子结点个数 = 左子树的左子树叶子结点个数 + 左子树的右子树叶子结点个数

右子树的叶子结点个数 = 右子树的左子树叶子结点个数 + 右子树的左子树叶子结点个数

不断套娃套娃

int BTLeafSize(BTNode* root)
{
	//访问到空结点，返回值0
	if (root == NULL)
		return 0;
	//如果是叶子结点  root->left == NULL root->right = NULL
	if (root->leftchild == NULL && root->rightchild == NULL)
		return 1;
	//计算对应左子树+右子树叶子结点并返回
	return BTLeafSize(root->leftchild) + BTLeafSize(root->rightchild);
}

4.求第K层结点的个数

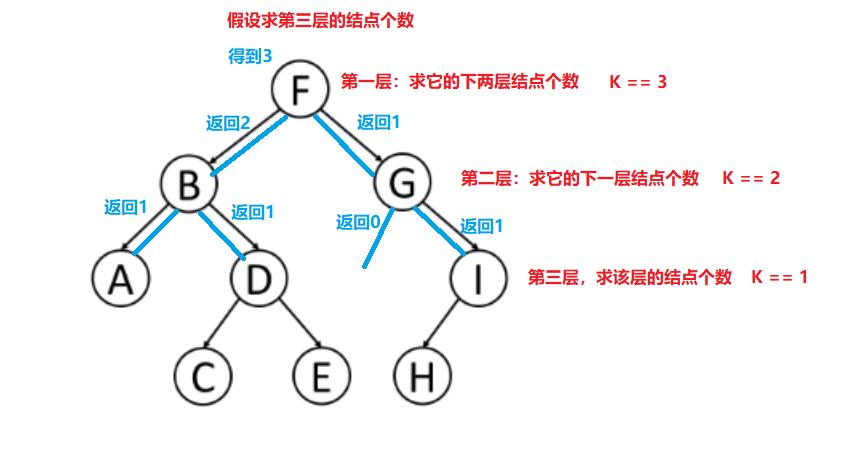
hehe还是一样，直接去求第K层的结点个数对于二叉树来说是很难做到的，我还是需要用分治的思想，使用递归的方式来解决问题。
hehe求相对于第一层求第K层，就是先对于第二层求K-1层……直到K=1时，转变成求该层的结点个数，这样就把问题彻底拆解，变成小问题了。

int BTKLevelSize(BTNode* root, int k)	//k值代表层数
{
	if (root == NULL)	//当访问到空时，说明无，返回0
		return 0;
	if (k == 1)		//k == 1时说明，到达所求层，并且该层有一个所求结点，返回1
		return 1;
	return BTKLevelSize(root->leftchild, k - 1) + BTKLevelSize(root->rightchild, k - 1);	//k != 1说明还没到所求的层数，则返回该结点左右子树的第k-1层结点数
}

二叉树的OJ练习

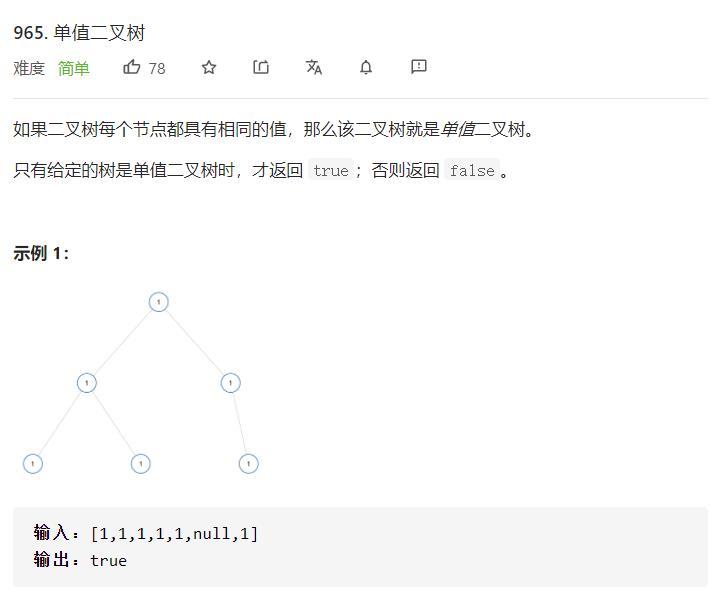
单值二叉树

题目描述

问题分析：

hewh该题目是判断这棵树所有结点的值是否相同，按照大问题转化为小问题的思想，那就是判断，一个结点的值与它左右孩子的值是否相同，如果每一个结点的值都与自己左右孩子结点的值相同，那么整棵树每个结点的值都相同。
hewh所以，小问题就是判断“根节点”的值与左右孩子值是否相等，再判断，左右孩子值是否与左右孩子的左右孩子值相等，这样不断递归，就完成了整棵树的判断。

代码实现：

bool isUnivalTree(struct TreeNode* root)
{
//访问到空，直接返回真
    if(root == NULL)	
        return true;
    //首先要判断left是否为空，因为如果是空的话，无法解引用
    //再判断根与左孩子值是否相等
    //注：如果判断是相等，那么无法拿出结果，还要继续往下判断直到结束
    //所以我们需要判断是否不等，有一个不等就说明不是单值，直接返回false
    if(root->left && root->left->val != root->val)	
        return false;
    //右孩子与左孩子同理
    if(root->right && root->right->val != root->val)
        return false;
    //走到这里说明该结点与它的左右孩子值相等，这时就要继判断左右孩子的
    //左右孩子值与各自双亲结点值是否相等，就要递归。
    //因为有一个不相等就返回false，所以用&&连接
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

2.二叉树的最大深度

题目描述

问题分析：

hewh求整棵树的最大深度，就是求树的高度，还是按照将问题分解，问题小化的原则。求树的最大高度，那么就要去求左右子树的高度中最大的+1，就得到整棵树的高度。同样左右子树的高度就是它们各自的左右子树的高度的最大值+1……如此循环往复。

代码实现：

//求最大值的函数，用于求左右子树中高度最大的
int Max(int a,int b)
{
    return a>b?a:b;
}
int maxDepth(struct TreeNode* root){
	//如果是空，说明高度为0，返回0
    if(root == NULL)
        return 0;
    //返回左右子树中最大的+1（自己这一层）
    return Max(maxDepth(root->left),maxDepth(root->right))+1;
}