多渠道归因分析：python实现马尔可夫链归因

Posted 2021-05-29 悟乙己

本篇主要是python实现马尔科夫链归因，关联的文章：

• 多渠道归因分析（Attribution）：传统归因（一）
• 多渠道归因分析：互联网的归因江湖（二）
• 多渠道归因分析：python实现马尔可夫链归因（三）

---

文章目录

• 1 关联理论
• • 1.1 渠道贡献度与移除效应
  • 1.2 absorption_matrix 吸收矩阵
• 2 R语言实现
• 3 python复现
• • 3.1 函数输出内容
  • 3.2 (核心思路)removal effect
  • 3.2 markov_conversions 马尔科夫转化率
  • 3.3 base_cvr
  • 3.4 吸收矩阵
  • 3.5 markov-chain-attribution代码
  • 3.6 MarkovAttribution库代码
  • 3.7 ChannelAttribution库

---

1 关联理论

参考：数据运营36计：马尔可夫链对营销渠道归因建模，R语言实现

马尔可夫链是一个过程，它映射运动并给出概率分布，从一个状态转移到另一个状态。马尔可夫链由三个属性定义：

• 状态空间：处理可能存在的所有状态的集合
• 转移概率：从一个状态转移到另一个状态的概率
• 当前状态分布 - 在过程开始时处于任何一个状态的概率分布

那么用户行为路径中的每个渠道可以看作这里的每个状态。在知道状态空间的情况下，所求的渠道贡献率就是每条路径的转移概率。所以马尔可夫链模型可以用来做归因分析。

1.1 渠道贡献度与移除效应

假设用户X的步骤如下：A > B > C > D > E > F > G. 4阶马尔可夫模型会显示用户X来自A(A> B > C > D)，然后经过序列B (B > C > D > E)，再到序列C (C > D > E > F),等等,直到用户X退出或转换。马尔可夫模型这里的阶数参数决定了用户现在的状态或所处阶段是由过去几个阶段决定的。但是这里决定阶数比较困难，一种方法是通过将设置多个阶数模型来绘制训练模型的误差，选取误差小的模型，从而确定模型的阶数。

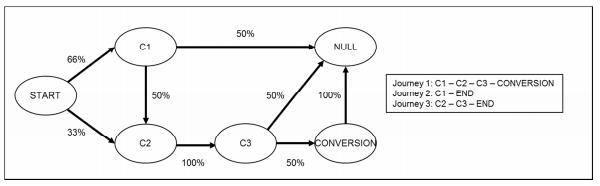
在上述情况下，客户可以通过渠道’C1’或渠道’C2’开始他们的路径。以C1或C2开始的概率为50％（或0.5）。我们首先计算转换的总体概率，然后进一步查看每个渠道的影响。

P（转换）= P（C1→C2→C3→转换）+ P（C2→C3→转换）
= 0.5 * 0.5 * 1 * 0.6 + 0.5 * 1 * 0.6
= 0.15 + 0.3
= 0.45

如果要弄清楚渠道C1在用户转化路径中的贡献，使用移除效应原则。即如果想要在用户路径中找到某个渠道的贡献，可以通过删除该渠道并查看在没有该渠道的情况下发生了多少次转化。

P（去除C1后的转换）= P（C2→C3→转换）

= 0.5 * 1 * 0.6

= 0.3

30％的用户互动可以在没有渠道C1的情况下进行转换; 而C1完好无损，45％的互动可以转换。所以，C1的移除效应是0.3 /0.45= 0.67。C2和C3的移除效应可以直接得出为1。那么渠道C1贡献度为0.67/(0.67+1+1)=25%, 同理C2=C3=37.5%。

**这是马尔可夫链的一个非常有用的应用。**在上述情况下，所有渠道C1，C2，C3（在不同阶段）被称为转换状态 ; 而从一个渠道转移到另一个渠道的概率称为转移概率。用户路径是由一系列渠道组成的，可以看作是一个有向马尔可夫图中的一个链，其中每个顶点都是一个状态（渠道），每条边表示从一个状态移动到另一个状态的转移概率（渠道转化率）。由于到达状态的概率仅取决于以前的k阶状态，因此可以将其视为无记忆马尔可夫链。

1.2 absorption_matrix 吸收矩阵

参考：吸收马尔可夫链还有一篇论文：吸收态马尔可夫链及其应用

在马尔可夫链中，称Pij=1的状态为吸收状态。如果一个马尔可夫链中至少包含一个吸收状态，并且从每一个非吸收状态出发，都可以到达某个吸收状态，那么这个马尔可夫链称为吸收马尔可夫链（Absorbing Markov Chains）

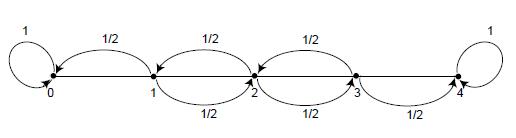
在上图的醉汉游走模型中，当醉汉处于位置1、2或者3时，他将会以等概率（1/2）向左或者向右走，他一直走，直到他到达位置0（他的家）或者位置4（酒吧）才停止游走。这模型的转移矩阵为：

含有r个吸收状态和t个非吸收状态的吸收链，其转移矩阵的标准形式为：

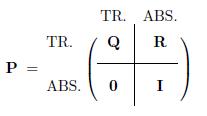
从状态1、2和3出发，到达吸收状态的平均转移次数分别为3、4和3。

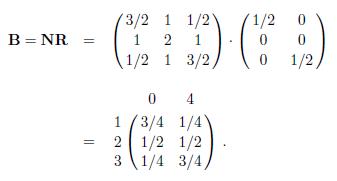
由矩阵B的第一行可知，从状态1出发，有3/4的概率到达吸收状态0，有1/4的概率到达吸收状态4。

论文：吸收态马尔可夫链及其应用中的一则使用：

---

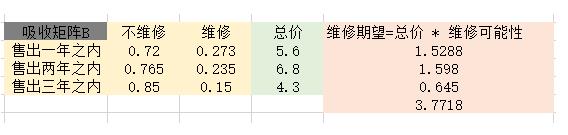
2 R语言实现

基本，参考：数据运营36计：马尔可夫链对营销渠道归因建模，R语言实现

官方论文：
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2343077
博客链接：
https://nelson.eu.org/how-to-use-markov-chains-for-attribution/
官方代码：
https://github.com/jerednel/markov-chain-attribution

这个模型在R语言里面很早就存在，包的名称为:ChannelAttribution,
关于这个库的有两篇非常好的教程：

• Marketing Multi-Channel Attribution model with R (part 1: Markov chains concept)

Marketing Multi-Channel Attribution model with R (part 2: practical issues)
还有一篇类似的：

Marketing Channel Attribution With Markov Models In R

这几篇博客，随便diss了一下GA分析：

众所周知，客户在电子商务购买或其他领域的转换之前通常会经历不同渠道/接触点的路径/顺序。
在Google Analytics（分析）中，我们发现某些接触点比其他更可能是最终点击接触点更有助于转化。由于大多数渠道是有偿的（根据金钱或花费的时间），因此至关重要的是，有一种算法可以在这些渠道之间分配转化次数和价值，并与它们的费用进行比较，而不是将其记入仅最后一个非直接渠道。这是一个多渠道归因模型问题。

Google Analytics（分析）的定义有助于：归因模型是一个或一组规则，用于确定如何将销售和转化功劳分配给转化路径中的接触点。

如今，Google Analytics（分析）提供了七个预定义的归因模型，甚至可以定制的自定义模型。
但是，我不喜欢Google Analytics（分析）方法的某些方面，这就是为什么我开始对此领域进行研究的原因。
我对GA方法不满意的地方：

• 您必须对使用哪种模型以及为什么使用做出选择或管理决策。您可以使用不同的模型看到不同的结果，但是哪一个更正确？换句话说，GA提供了启发式模型及其优缺点
• 数据经过汇总和匿名处理，如果您愿意，则无法深入挖掘
• 您无法考虑没有转化的路径，但这很有趣。

其中，博文Marketing Multi-Channel Attribution model with R (part 2: practical issues)有非常完整的分析流程：

我们将审查的主要步骤如下：

• 根据购买数量划分路径
• 更换一些频道/触点
• 独特的频道/接触点案例
• 路径和高阶马尔可夫链中的后续复制信道
• 未导致转换的路径
• 客户行程持续时间
• 收入和成本比较

3 python复现

复现的github上有两个：

• jerednel/markov-chain-attribution
• dsearle90/MarkovAttribution
  可能markov-chain-attribution更好一些

3.1 函数输出内容

输出内容解释：

• markov_conversions，代表的是不同转化路径全局贡献，有点像是PCA中的主成分贡献比率；这个是在removal_effects基础上进行计算的
• base_cvr，成功转化路径 / 总路径
• removal_effects，该模型的核心，不同路径/渠道的重要性，手法是去除这个渠道看整个链路最终转化链路的损失程度
• last_touch_conversions，最后一步触达转化的渠道/路径有哪些，触达次数是多少
• transition_matrix，状态转移概率矩阵，常见
• absorption_matrix，吸收态概率矩阵，描绘的是不同渠道/路径对最终转化状态的转移可能性，可以用来衡量多渠道/路径的价值或成本估算；可能c1->c2->conv，这个概率矩阵，可以综合中间层的结论，直接导向：c1 -> conv

markov_conversions和absorption_matrix的差异：
同是重要性，不过各有差异，出发点不同

• markov_conversions，是基于移除效应的重要性，是相对量，且针对的是转化这个单一状态
• absorption_matrix，包括了到转化的可能性，也是一种重要性，且基本结论跟markov_conversions一致，只不过更有意义的是，这个概率可以被累加

举例输出：

{'markov_conversions': {'晴天': 0.2, '阴天': 0.4, '雨天': 0.4},
 'last_touch_conversions': {'晴天': 0, '阴天': 1, '雨天': 0},
 'removal_effects': {'晴天': 0.5, '阴天': 1.0, '雨天': 1.0},
 'base_cvr': 0.3333333333333333,
 'transition_matrix':              晴天   阴天  null        雨天  conv  start
 晴天     0.000000  0.0   0.5  0.500000   0.0    0.0
 阴天     0.000000  0.0   0.5  0.000000   0.5    0.0
 null   0.000000  0.0   1.0  0.000000   0.0    0.0
 雨天     0.000000  1.0   0.0  0.000000   0.0    0.0
 conv   0.000000  0.0   0.0  0.000000   1.0    0.0
 start  0.666667  0.0   0.0  0.333333   0.0    0.0,
 'absorption_matrix': array([[0.75      , 0.25      ],
        [0.5       , 0.5       ],
        [0.5       , 0.5       ],
        [0.66666667, 0.33333333]])}

3.2 (核心思路)removal effect

当我们移除某个channels,我们整个系统会有什么影响？找到channels对整个链路的贡献
这个概率矩阵，它被定义为当给定的信道或策略从系统中移除时达到转换的概率。
操作方式为that channel is set to 100% no conversion，设置当下效果，转化率为0，那么就会获得一个新的模型
最后比较的方式为：

从数学上讲，比较的是，原有系统的转换率与设置channel后的系统的转换率之间的百分比差异。
然后，我们将去除率CVR除以每个通道的所有去除率CVR的总和，以得到每个权重的权重，这样我们最终可以将该数字乘以转化次数，得出转化的部分归因数量。

来看一个计算实战case：

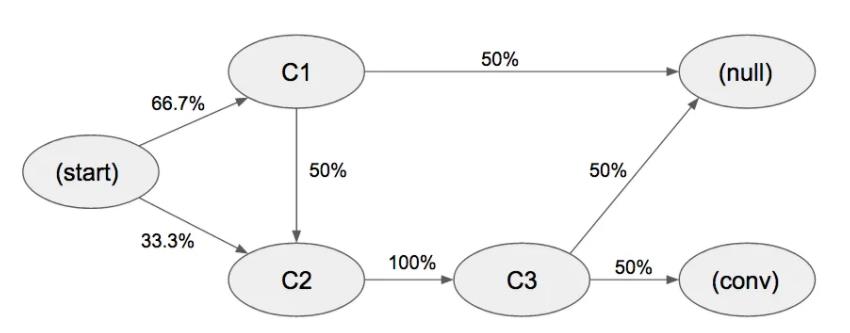
原本c1的效用（指的是到转化的效用，不是null，所以不走start -> c1 -> null这条路 ）为：
0.667 * 0.5 * 1 * 0.5 + 0.333 * 1 * 0.5 = 33.3%

c2的效用：
0.333*1*0.5 = 0.1165

现在去掉c1
0.333*1*0.5 = 16.5%
去掉c2/c3:0

所以，c1的贡献为：

0.5 = 1 – 0.167 / 0.333
c2/c3的贡献都为1

大概意思为：

• 如果没有c2/c3，发生转化的可能性为0，贡献率 = 1；
• 如果没有c1，贡献率为0.5，发生转化的可能性为0.5

3.2 markov_conversions 马尔科夫转化率

需要对索引进行加权，然后将它们乘以总转化次数（在本例中为1）：
其中c1=0.5,c2=1,c3=1 都是基于上述removal effect，各个触点对整个网络的价值

C1: 0.5 / (0.5 + 1 + 1) = 0.2 * 1 conversion = 0.2
C2: 1 / (0.5 + 1 + 1) = 0.4 * 1 conversion = 0.4
C3: 1 / (0.5 + 1 + 1) = 0.4 * 1 conversion = 0.4

此时：last_touch_conversions，就是最后可以导向转化的c1,c2,c3的个数分别为：

c1 = 0
c2 = 0
c3 = 1

3.3 base_cvr

base_cvr = 转化的路径个数 / 总路径个数 = 1 / 3 = 0.333

3.4 吸收矩阵

它是由两个矩阵相乘，链各个状态分别是：不转化 + 转化，四个基本状态为：cone,ctwo,start,cthree

# N矩阵
array([[1.        , 0.5       , 0.        , 0.5       ],
       [0.        , 1.        , 0.        , 1.        ],
       [0.66666667, 0.66666667, 1.        , 0.66666667],
       [0.        , 0.        , 0.        , 1.        ]])

            cone      ctwo  start  cthree
cone    0.000000  0.500000    0.0     0.0
ctwo    0.000000  0.000000    0.0     1.0
start   0.666667  0.333333    0.0     0.0
cthree  0.000000  0.000000    0.0     0.0

# R矩阵
        null  conv
cone     0.5   0.0
ctwo     0.0   0.0
start    0.0   0.0
cthree   0.5   0.5

# B - 吸收态矩阵
            null      conv
ctwo    0.500000  0.500000
cone    0.750000  0.250000
start   0.666667  0.333333
cthree  0.500000  0.500000

从状态ctwo达到状态null的概率为0.5，cone达到conv的状态概率为0.25
假设一个场景是，cone,ctwo,start,cthree都是媒体触点，都是计费的，不同触点的价格：

ctwo = 2 
cone = 1 
start = 4 
cthree = 3

我们希望本次活动有100个人可以实现最终的转化，那么本次需要投入的总费用：
20.5 + 10.25 + 4 * 0.33 + 3 *0.5 = 4.07
100个人的总费用为：100*4.07 = 407元

3.5 markov-chain-attribution代码

对jerednel/markov-chain-attribution代码进行两处的微调:

• 接受中文输入\\u4e00-\\u9fa5
• absorption_matrix 吸收态转移矩阵，带上dataframe的列名/行名

import pandas as pd
import numpy as np
import re
import copy

def run_model(paths):
    regex = re.compile('[^a-zA-Z> | \\u4e00-\\u9fa5 ]')
    paths.rename(columns={paths.columns[0]: "Paths"}, inplace=True)
    paths['Paths'] = paths['Paths'].apply(lambda x: regex.sub('', x))
    markov_conversions = first_order(paths)
    return markov_conversions


def calculate_removals(df, base_cvr):
    # df = test_df
    removal_effect_list = dict()
    channels_to_remove = df.drop(['conv', 'null', 'start'], axis=1).columns
    # channels_to_remove  = ['cone','ctwo','cthree']
    for channel in channels_to_remove:
        removal_cvr_array = list()
        removal_channel = channel
        removal_df = df.drop(removal_channel, axis=1)
        removal_df = removal_df.drop(removal_channel, axis=0)
        for col in removal_df.columns:
            one = float(1)
            row_sum = np.sum(list(removal_df.loc[col]))
            null_percent = one - row_sum
            if null_percent == 0:
                continue
            else:
                removal_df.loc[col]['null'] = null_percent
        removal_df.loc['null']['null'] = 1.0
        R = removal_df[['null', 'conv']]
        R = R.drop(['null', 'conv'], axis=0)
        Q = removal_df.drop(['null', 'conv'], axis=1)
        Q = Q.drop(['null', 'conv'], axis=0)
        t = len(Q.columns)

        N = np.linalg.inv(np.identity(t) - np.asarray(Q))
        M = np.dot(N, np.asarray(R))
        removal_cvr = pd.DataFrame(M, index=R.index)[[1]].loc['start'].values[0]
        removal_effect = 1 - removal_cvr / base_cvr
        removal_effect_list[channel] = removal_effect
    return removal_effect_list


def first_order(paths):
    paths = np.array(paths).tolist()
    sublist = []
    total_paths = 0
    for path in paths:
        for touchpoint in path:
            userpath = touchpoint.split(' > ')
            sublist.append(userpath)
        total_paths += 1
    paths = sublist

    unique_touch_list = set(x for element in paths for x in element)
    # get total last touch conversion counts
    conv_dict = {}
    total_conversions = 0
    for item in unique_touch_list:
        conv_dict[item] = 0
    for path in paths:
        if 'conv' in path:
            total_conversions += 1
            conv_dict[path[-2]] += 1

    transitionStates = {}
    base_cvr = total_conversions / total_paths
    for x in unique_touch_list:
        for y in unique_touch_list:
            transitionStates[x + ">" + y] = 0

    for possible_state in unique_touch_list:
        if possible_state != "null" and possible_state != "conv":
            # print(possible_state)
            for user_path in paths:

                if possible_state in user_path:
                    indices = [i for i, s in enumerate(user_path) if possible_state == s]
                    for col in indices:
                        transitionStates[user_path[col] + ">" + user_path[col + 1]] += 1

    transitionMatrix = []
    actual_paths = []
    for state in unique_touch_list:

        if state != "null" and state != "conv":
            counter = 0
            index = [i for i, s in enumerate(transitionStates) if s.startswith(state + '>')]
            for col in index:
                if transitionStates[list(transitionStates)[col]] > 0:
                    counter += transitionStates[list(transitionStates)[col]]
            for col in index:
                if transitionStates[list(transitionStates)[col]] > 0:
                    state_prob = float((transitionStates[list(transitionStates)[col]])) / float(counter)
                    actual_paths.append({list(transitionStates)[col]: state_prob})
    transitionMatrix.append(actual_paths)

    flattened_matrix = [item for sublist in transitionMatrix for item in sublist]
    transState = []
    transMatrix = []
    for item in flattened_matrix:
        for key in item:
            transState.append(key)
        for key in item:
            transMatrix.append(item[key])

    tmatrix = pd.DataFrame({'paths': transState,
                            'prob': transMatrix})
    # unique_touch_list = model['unique_touch_list']
    tmatrix = tmatrix.join(tmatrix['paths'].str.split('>', expand=True).add_prefix('channel'))[
        ['channel0', 'channel1', 'prob']]
    column = list()
    for k, v in tmatrix.iterrows():
        if v['channel0'] in column:
            continue
        else:
            column.append(v['channel0'])
    test_df = pd.DataFrame()
    for col in unique_touch_list:
        test_df[col] = 0.00
        test_df.loc[col] = 0.00
    for k, v in tmatrix.iterrows():
        x = v['channel0']
        y = v['channel1']
        val = v['prob']
        test_df.loc[x][y] = val
    test_df.loc['conv']['conv'] = 1.0
    test_df.loc['null']['null'] = 1.0
    R = test_df[['null', 'conv']]
    R = R.drop(['null', 'conv'], axis=0)
    Q = test_df.drop(['null', 'conv'], axis=1)
    Q = Q.drop(['null', 'conv'], axis=0)
    O = pd.DataFrame()
    t = len(Q.columns)
    for col in range(0, t):
        O[col] = 0.00
    for col in range(0, len(R.columns)):
        O.loc[col] = 0.00
    N = np.linalg.inv(np.identity(t) - np.asarray(Q))
    M = np.dot(N, np.asarray(R))
    
    # 给M带上属性
    _R = copy.deepcopy(R)
    for n in range(len(R.columns)):
        _R[_R.columns[n]] = M[:,n]
        _R[_R.columns[n]] = M[:,n]
    _M = _R
    
    base_cvr = pd.DataFrame(M, index=R.index)[[1]].loc['start'].values[0]
    removal_effects = calculate_removals(test_df, base_cvr)
    denominator = np.sum(list(removal_effects.values()))
    allocation_amount = list()
    for i in removal_effects.values():
        allocation_amount.append((i / denominator) * total_conversions)
    # print(allocation_amount)
    markov_conversions = dict()
    i = 0
    for channel in removal_effects.keys():
        markov_conversions[channel] = allocation_amount[i]
        i += 1
    conv_dict.pop('conv', None)
    conv_dict.pop('null', None)
    conv_dict.pop('start', None)

    return {'markov_conversions': markov_conversions,
            'last_touch_conversions': conv_dict,
            'removal_effects': removal_effects,
            'base_cvr': base_cvr,
            'transition_matrix': test_df,
            'absorption_matrix': _M
}

两个案例，一个英文：

import pandas as pd

# generate a sample dataset
df = pd.DataFrame({'Paths':['start > cone > ctwo > cthree > conv',
                           'start > cone > null',
                           'start > ctwo > cthree > null']})

model = run_model(paths=df)
paths = df

# 转移概率 
model['transition_matrix']
    
# absorption matrix
model['absorption_matrix']

'''
       null  conv
cone    0.5   0.0
ctwo    1.0   0.0
start   0.0   0.0


array([[0.75      , 0.25      ],
       [0.5       , 0.5       ],
       [0.66666667, 0.33333333],
       [0.5       , 0.5       ]])


'''

model['absorption_matrix'].mean(axis = 0)



# base_cvr = 转化的路径个数 / 总路径个数
1 / 3

# last_touch_conversions 最后一个路径下的
{'cone': 0, 'ctwo': 0, 'cthree': 1}
    

还有一个中文：

#
#
#import pandas as pd
#
## generate a sample dataset
#df = pd.DataFrame({'Paths':['start > 晴天 > 雨天 > 阴天 > conv',
#                           'start > 晴天 > null',
#                           'start > 雨天 > 阴天 > null']})
#
#model = run_model(paths=df)
#model

3.6 MarkovAttribution库代码

新的地址：
https://github.com/dsearle90/MarkovAttribution

• Specify custom processing of leftover removal distribution
  • 移除效应的自定义处理
• Two methods of removal effect calculation available – Channel synthesis – Direct approximation
  • 两种移除效应的计算模式

模型参数：

• conversion_col ：转化率的一列，This column should be of type string and only contain either ‘conv’ or ‘null’
• path_prefix :文件地址
• removal_calc_mode ，移除效应计算模型：approximate / synthesize

Options are ‘approximate’ and’synthesize’ Approximate uses linear algebra to directly calculate removal effects, whereas synthesize will generate synthetic user journeys based off the removal transition matrix. ‘Approximate’ generates much faster results

• removal_leftover_redist 移除效应，填补模式：default “null”

Options are ‘null’ and ‘even’ When removing a channel, we must decide how to re-allocate the missing % of journeys. Null will directly re-assign any leftover probability to a non-conversion (null). Even will scale up and re-allocate across existing channels based on their current probability.
当删除一个通道时，我们必须决定如何重新分配丢失的%的旅程。
Null将直接将剩余的概率重新分配给非转换(Null)。甚至将扩大和重新分配现有渠道的基础上，目前的可能性。

3.7 ChannelAttribution库

刚刚提到的R语言实现的那款，也有python，不过没有什么教程
笔者在这也就不展开了
可参考：
官网：https://www.channelattribution.net/docs/gettingstarted
PDF教程：https://www.channelattribution.net/assets/files/ChannelAttributionWhitePaper-0536c269c4725179d4a0d8b8ec2f0fac.pdf
python教程：https://www.channelattribution.net/assets/files/PythonChannelAttribution-c98a8c4eabed0dfd58083870dc807ee0.pdf
代码源：https://gitlab.com/session-tech/ChannelAttribution

安装：

pip install --upgrade setuptools
pip install Cython
pip install ChannelAttribution

简单实现：

 import pandas as pd

from ChannelAttribution import *
Data = pd.read_csv('http://www.channelattribution.net/csv/Data.csv',sep=";")
# auto_markov_model
auto_markov_model(Data, "path", "total_conversions", "total_null")
# heuristic_models
heuristic_models(Data,"path","total_conversions")

heuristic_models指的就是首次点击模型，末尾点击模型，平均点击模型