优化求解狼群优化算法matlab源码
Posted Matlab咨询QQ1575304183
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优化求解狼群优化算法matlab源码相关的知识,希望对你有一定的参考价值。
1 狼群算法的优缺点
狼群算法是一种随机概率搜索算法,使其能够以较大的概率快速找到最优解;狼群算法还具有并行性,可以在同一时间从多个点出发进行搜索,点与点之间互不影响,从而提高算法的效率。
将WPA算法应用于15个典型复杂函数优化问题,并同经典的粒子群算法、鱼群算法和遗传算法进行比较仿真结果表明,该算法具有较好的全局收敛性和计算鲁棒性,尤其适合高维、多峰的复杂函数求解。
1.1 狼群算法的优点
狼群算法是一种随机概率搜索算法,使其能够以较大的概率快速找到最优解;狼群算法还具有并行性,可以在同一时间从多个点出发进行搜索,点与点之间互不影响,从而提高算法的效率。将WPA算法应用于15个典型复杂函数优化问题,并同经典的粒子群算法、鱼群算法和遗传算法进行比较仿真结果表明,该算法具有较好的全局收敛性和计算鲁棒性,尤其适合高维、多峰的复杂函数求解。
1.2 狼群算法的缺点
WPA算法“寻优过程分为游走、奔袭和围攻,人工狼之间缺少必要的信息交流,算法全局性不高,过于分散”的不足之处出发,对算法进行改进。探狼是随机选择h个方向然后进行探索,互相之间并没有交流,探索空间会存在重复。目前的狼群智能算法很难找到全局最优解,不断探索群智能优化算法已成为许多学者研究的热点问题。
2 狼群算法的仿真验证
通过8个高维复杂函数对一种新型仿生群体智能算法—狼群算法(WPA)进行仿真验证,并与粒子群优化(PSO)算法进行对比。针对BP神经网络易陷入局部极值及初始权闰值参数难以确定的不足,利用WPA算法优化BP神经网络初始参数,提出WPA一BP径流预测模型,以云南省龙潭站枯水期月径流预测为例进行实例验证,并与PSO一BP及BP模型进行比较。结果表明:
①WPA算法收敛精度远远优于PSO算法,具有较好的计算鲁棒性和全局寻优能力;②WPA一BP模型预测精度优于PSO一BP及BP模型,具有较好的预测精度和泛化能力。利用WPA算法优化BP神经网络的初始权值和闰值,可有效提高BP神经网络的预测精度和泛化能力。
2.1 狼群算法
狼群算法通过初始化狼群、竞争头狼、头狼召唤、围攻猎物以及狼群更新5个步骤来实现求解最优化问题,狼群算法步骤如下:
Step1 初始化。设人工狼群规模为N,搜索空间的维数为D,第i只人工狼的空间位置可表示为:
(1)
(2)
式中 rand为[0,1]之间的随机数;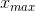 、
、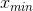 为搜索空间的上下限。
为搜索空间的上下限。
Step2 竞争头狼。选取适度值最好(位置最优)的q只人工狼作为竞争者,这q只人工狼在自己周围的h个方向进行搜索(游走),其所在位置为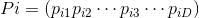 。设竞争狼的当前位置是
。设竞争狼的当前位置是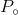 ,
,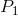 是围绕当前位置
是围绕当前位置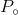 产生的。若
产生的。若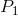 的位置优于
的位置优于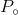 ,则将竞争狼的
,则将竞争狼的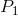 位置作为当前位置,并继续搜索。当竞争狼搜索(游走)次数大于最大游走次数
位置作为当前位置,并继续搜索。当竞争狼搜索(游走)次数大于最大游走次数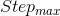 或搜索到的位置劣于当前位置时,则竞争狼的搜索(游走)行为结束,并将当前最优位置的竞争狼作为头狼,头狼以外最佳的(q-1)只人工狼视为探狼。探狼取
或搜索到的位置劣于当前位置时,则竞争狼的搜索(游走)行为结束,并将当前最优位置的竞争狼作为头狼,头狼以外最佳的(q-1)只人工狼视为探狼。探狼取[n/(
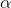 +1),n/
+1),n/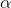 ]之间的随机数,
]之间的随机数,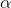 为探狼比例因子。则探狼附近产生的h个点的位置中第j个点第d维的位置
为探狼比例因子。则探狼附近产生的h个点的位置中第j个点第d维的位置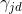
 (
(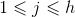 )可表示为:
)可表示为:
(3)
式中 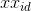 ——第i只探狼第d维的当前位置;
——第i只探狼第d维的当前位置;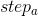 ——搜索(游走)步长。
——搜索(游走)步长。
Step3 头狼召唤。头狼通过嚎叫发起召唤行为,召集周围的k只猛狼向头狼所在位置靠拢,则猛狼i在第d维变量空间中第t+1次迭代所处的位置表示为:
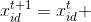
(4)
式中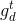 ——第t代狼群头狼在第d维空间的位置;
——第t代狼群头狼在第d维空间的位置;
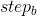 ——猛狼奔袭步长。
——猛狼奔袭步长。
猛狼奔袭途中,若猛狼i的位置优于头狼,则孟浪作为头狼发起召唤行为;否则,猛狼i继续奔袭直到其与头狼s之间的距离
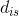 小于
小于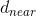 时加入到对猎物的围攻行为。设待寻优的第d维变量的取值范围为[
时加入到对猎物的围攻行为。设待寻优的第d维变量的取值范围为[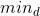 ,
,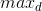 ],则判定距离
],则判定距离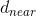 可用下式表示
可用下式表示
(5)
式中 ——距离判定因子。
——距离判定因子。
Step4 围攻猎物。将距离猎物较近的猛狼与探狼联合对猎物进行围攻,并将距离猎物最近的头狼的位置视为猎物的移动位置。对于第t代狼群,设猎物在第d维空间中的位置为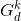 ,则狼群的围攻行为可表示为:
,则狼群的围攻行为可表示为:
(6)
式中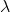 ——[-1,1]均匀随机分布的随机数;
——[-1,1]均匀随机分布的随机数;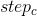 ——攻击步长。
——攻击步长。
在d维空间中,游走步长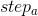 、奔袭步长
、奔袭步长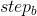 和攻击步长
和攻击步长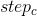 有如下关系:
有如下关系:
(7)
式中S——步长因子。
Step4 狼群更新机制。将狼群捕获的猎物按照“由强到弱”的原则进行分配,最终导致最弱小的狼被饿死,较强壮的狼能够继续生存下去,如此使狼群具有更好的适应能力。根据优胜劣汰的原则,在算法中移除目标函数最差的u只人工狼,然后通过式(2)随机生成u只新的人工狼,这样有利于维护狼的个体多样性,使得该算法不易陷入局部最优。u取[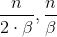 ],为群体更新比例因子。
],为群体更新比例因子。
2.2 狼群算法与WPA、PSO、FSA、GA算法的比较分析
为充分测试算法的性能和特点,通常要引入较多具有不同特征的标准函数,这里采用15个复杂函数作为实验对象,表中特征“U”表示此函数为单峰(Unimodal)函数,“M”表示多峰(Multimodal),“S”表示可分(Separable),“N”表示不可分(No-Separable)。
上述所选函数涉及单峰、多峰、可分、不可分等多种特征的复杂函数,多峰函数常用来检验算法的全局搜索性能和避免早熟收敛的能力,不可分函数变量间关系复杂,因此对此类函数寻优相对更加困难,搜索空间的维数也是个重要因素,很多对于低维函数效果很好的算法面对高维复杂函数其寻优效果却较差。表中函数的变量维数从2~200维,都是难度较大的复杂优化问题,具有很好的测试性,可较为全面的反映各算法的性能。利用表中15个复杂函数对WPA算法及PSO、FSA、GA进行比较分析。
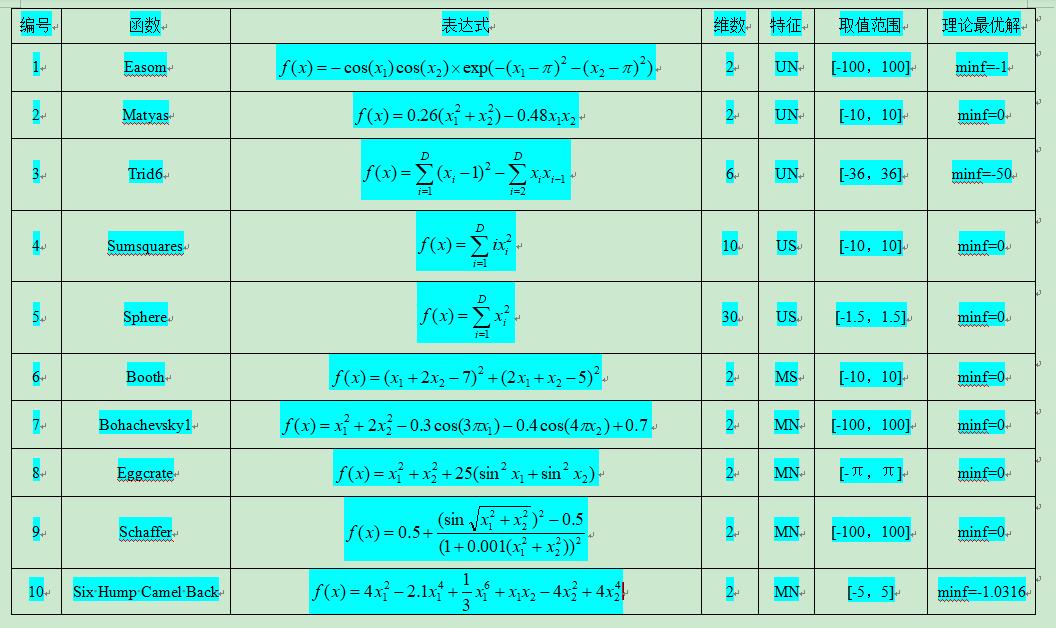

利用WPA、PSO、FSA、GA此4种智能算法分别对15个复杂函数重复进行100次寻优计算。从最优值、最差值、平均值、计算成功率、平均耗时等多方面对算法进行评估。这里,设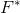 为每次寻优计算所得最有函数值,F为函数的理想最优值,当两者满足下式时,即视此次寻优计算成功。将寻优计算成功的次数除以总计算次数即为计算成功率,可较好地反应算法运算的稳定性和对抗局部极值的能力
为每次寻优计算所得最有函数值,F为函数的理想最优值,当两者满足下式时,即视此次寻优计算成功。将寻优计算成功的次数除以总计算次数即为计算成功率,可较好地反应算法运算的稳定性和对抗局部极值的能力
%% WPA算法
clear
close
clc
%% 初始化参数
wolfnum = 50;
maxgen = 300;
alfa = 4;
Tmax = 30;
omega = 100;
S = 1000;
beta = 10;
lb = -pi;
ub = pi;
stepa = (ub - lb)/S;
stepb = (ub - lb)/S*2;
stepc = (ub - lb)/(S*2);
hmax = 15;
hmin = 2;
%% 初始化狼群
X = lb + (ub - lb)*rand(wolfnum,1);
Y = objfunc(X);
[maxY,maxYindex] = max(Y);
maxX = X(maxYindex);
leadY = maxY;
leadX = maxX;
[Y,Yindex] = sort(Y,'descend');
X = X(Yindex);
plotx = linspace(-pi,pi,200);
ploty = objfunc(plotx);
plot(plotx,ploty);
hold on
hobj = plot(X,Y,'*');
for iter = 1 : maxgen
%% 游走
minSnum = ceil(wolfnum / (alfa + 1));
maxSnum = floor(wolfnum / alfa);
Snum = randi([minSnum,maxSnum],1,1);
flag = 0;
for i = 1 : Tmax
for j = 2 : Snum + 1 %探狼从第二只开始
h = randi([hmin,hmax]);
nextx = zeros(h,1);
nexty = zeros(h,1);
for k = 1 : h % 每一只狼游走h次
nextx(k) = X(j) + sin(2*pi*k/h) * stepa;
if nextx(k) < lb
nextx(k) = lb;
end
if nextx(k) > ub
nextx(k) = ub;
end
nexty(k) = objfunc(nextx(k));
end
[bestnexty,bestnextyindex] = max(nexty);
bestnextx = nextx(bestnextyindex);
if bestnexty > Y(j)
Y(j) = bestnexty;
X(j) = bestnextx;
end
if bestnexty > leadY
leadY = bestnexty;
leadX = bestnextx;
flag = 1;
break;
end
end
if flag == 1
break;
end
end
%% 召唤
for i = Snum + 1 + 1 : wolfnum
while 1
Mnextx = X(i) + stepb * (leadX - X(i))/(abs(leadX - X(i)));
if Mnextx < lb
Mnextx = lb;
end
if Mnextx > ub
Mnextx = ub;
end
Mnexty = objfunc(Mnextx);
X(i) = Mnextx;
Y(i) = Mnexty;
dis = abs(Mnextx - leadX);
dnear = 1/omega * (ub - lb);
if Mnexty > leadY
leadY = Mnexty;
leadX = Mnextx;
break;
elseif dis < dnear
Gnextx = X(i) + (2*rand -1)* stepc * abs((leadX - X(i)));
if Gnextx < lb
Gnextx = lb;
end
if Gnextx > ub
Gnextx = ub;
end
Gnexty = objfunc(Gnextx);
if Gnexty > Y(i)
Y(i) = Gnexty;
X(i) = Gnextx;
end
end
break;
end
end
hobj.XData = X;
hobj.YData = Y;
pause(0.02)
[Y,Yindex] = sort(Y,'descend');
X = X(Yindex);
R = randi([floor(wolfnum/(2*beta)),floor(wolfnum/(beta))]);
index = wolfnum:-1:wolfnum - R + 1;
X(index) = lb + (ub - lb)*rand(length(index),1);
Y(index) = objfunc(X(index));
leadX = X(1);
leadY = Y(1);
end
figure(2)
plot(Y)完整代码或仿真咨询QQ1575304183
以上是关于优化求解狼群优化算法matlab源码的主要内容,如果未能解决你的问题,请参考以下文章