Java 求解二叉树的所有路径

Posted 2021-05-29 南淮北安

文章目录

• • 一、题目
  • 二、题目分析
  • 三、递归法
  • 四、迭代法
  • 五、总结

一、题目

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

二、题目分析

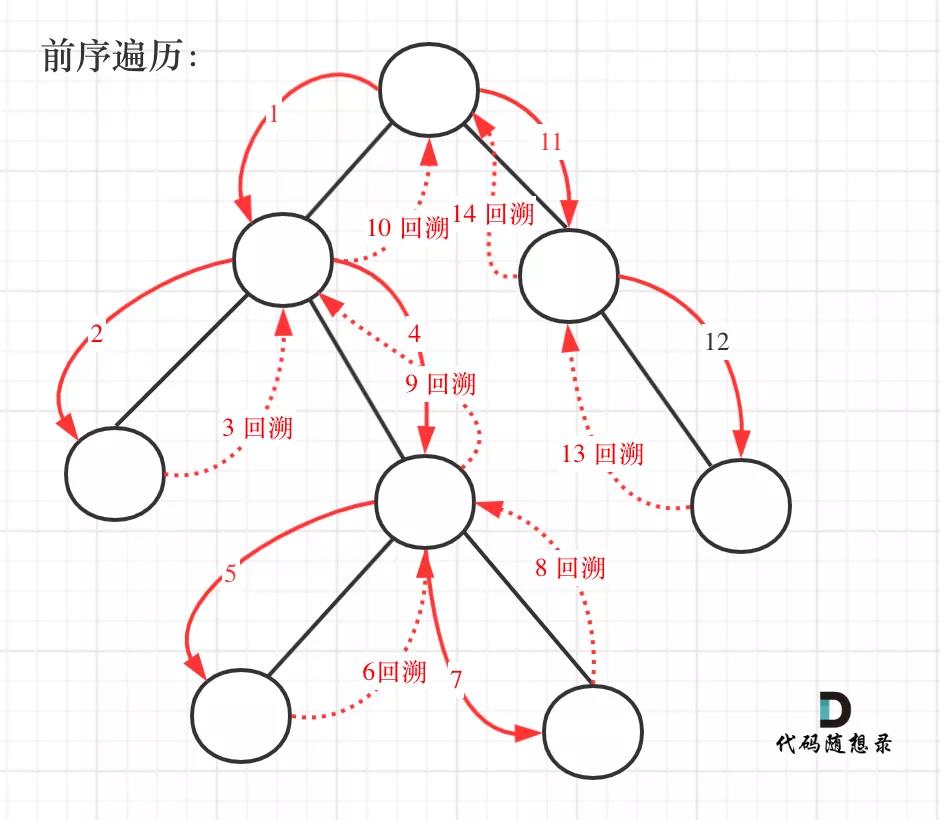
题目要求从根节点到叶子节点的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

前序遍历以及回溯的过程如图：

三、递归法

该题本质是回溯题，回溯和递归相辅相成

（1）回溯函数的参数及返回值

//存放所有的结果值
List<String> list = new ArrayList<>();
//存放每次的结果值
Deque<TreeNode> deque = new LinkedList<>();

（2）确定回溯终止条件

由于本题查找是路径问题，所以当走到叶子节点时，回溯终止，记录一次结果

if (root.left != null && root.right != null) {
}

（3）确定遍历过程

由于采用的是先序遍历的思想，所以先处理中间节点，然后是递归和回溯

class Solution {
    //存放所有的结果值
    List<String> list = new ArrayList<>();
    //存放每次的结果值
    Deque<TreeNode> deque = new LinkedList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) {
            return list;
        }
        backTracking(root);
        return list;
    }

    public void backTracking(TreeNode root) {
        deque.add(root);
        if (root.left == null && root.right == null) {
            String str = "";
            for (TreeNode node : deque) {
                str += node.val;
                str += "->";
            }
            //移除最后添加的 "->"
            list.add(str.substring(0, str.length() - 2));
        }
        if (root.left != null) {
            backTracking(root.left);
            //回溯
            deque.removeLast();
        }
        if (root.right != null) {
            backTracking(root.right);
            //回溯
            deque.removeLast();
        }
    }
}

精简版：

class Solution {

    List<String> list = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) {
            return list;
        }
        String path = "";
        backTracking(root, path);
        return list;
    }

    public void backTracking(TreeNode root, String path) {
        path += root.val;
        if (root.left == null && root.right == null) {
            list.add(path);
        }
        if (root.left != null) {
            //每次回溯完，path是没有加上"->"的，完成回溯的工作
            backTracking(root.left, path + "->");
        }
        if (root.right != null) {
            backTracking(root.right, path + "->");
        }
    }
}

四、迭代法

借助栈实现先序遍历，同时需要一个栈记录每个节点对应的遍历路径

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        //记录先序遍历
        Deque<TreeNode> deque = new LinkedList<>();
        //记录遍历的节点对应的路径
        Deque<String> pathDeque = new LinkedList<>();
        String path;
        TreeNode node;
        deque.push(root);
        pathDeque.push(root.val + "");
        while (!deque.isEmpty()) {
            node = deque.pop();
            path = pathDeque.pop();
            //遇到叶子节点，存储该路径
            if (node.left == null && node.right == null) {
                list.add(path);
            }
            if (node.right != null) {
                deque.push(node.right);
                pathDeque.push(path + "->" + node.right.val);
            }
            if (node.left != null) {
                deque.push(node.left);
                pathDeque.push(path + "->" + node.left.val);
            }
        }
        return list;
    }
}

五、总结

求解二叉树的所有路径，即根节点到叶子节点的所有路径，采用先序遍历

本质是一个回溯，注意对路径的处理