SCAU18747 关键路径

Posted 2021-05-29 吃花椒的妙酱

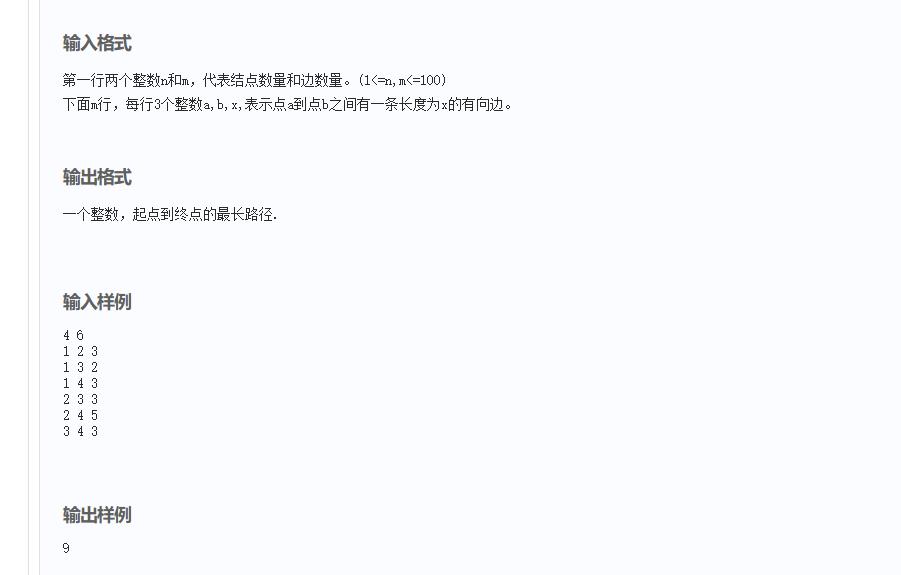
思路：求最长路

所谓关键路径即影响最大的路径，即求代价最大的路径，将问题转化成求最长路

最长路，我们可以用spfa求（迪杰斯特拉不行，正数跑的贪心是错的，跑负权边的话不满足算法的先决条件

#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <map>
#include <vector>
#include <queue>
using namespace std;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pb push_back
#define IOS ios::sync_with_stdio(false)
#define int long long
#define inf 0x3f3f3f3f
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
typedef long long ll;
const int N=1e6+10;
int n,m;
struct ty
{
    int t,next,val;//边的编号，下个边，边权
}edge[N];
int tot,head[N];
void addedge(int x, int y, int z)
{
    edge[++tot].t=y;
    edge[tot].val = z;
    edge[tot].next=head[x];
    head[x]=tot;
}
queue <int > q;
int v[N];//当前点是否在队列中
int dis[N];//当前点与起点的距离
void spfa()
{
    q.push(1);//起点入队
    v[1]=1;
    while( !q.empty() )
    {
        int x = q.front();//取队首
        q.pop();
        v[x]=0;
        for(int i=head[x] ;i!=0 ;i=edge[i].next)
        {
            int y = edge[i].t;//当前点的儿子
            int len = edge[i].val;
            if( dis[x] + len > dis[y] )//更新儿子的距离
            {
                dis[y] = dis[x] + len;
                if( !v[y] )//若不在队列里，儿子入队，因为儿子的dis改变后对儿子的儿子有影响,要重新更新
                {
                    v[y]=1;q.push(y);
                }
            }
        }
    }
    cout<<dis[n]<<endl;//输出终点距离
}
signed main()
{
    ///!!!
//    freopen("data.txt","r",stdin);
//    !!!
    IOS;
    cin>>n>>m;
    _for(i,1,m)
    {
        int x,y,z;
        cin>>x>>y>>z;
        addedge(x,y,z);
    }
    spfa();
}