leetcode 37. 解数独----回溯篇1

Posted 2021-05-29 大忽悠爱忽悠

---

解数独题解集合

• 回溯法
• 位运算

---

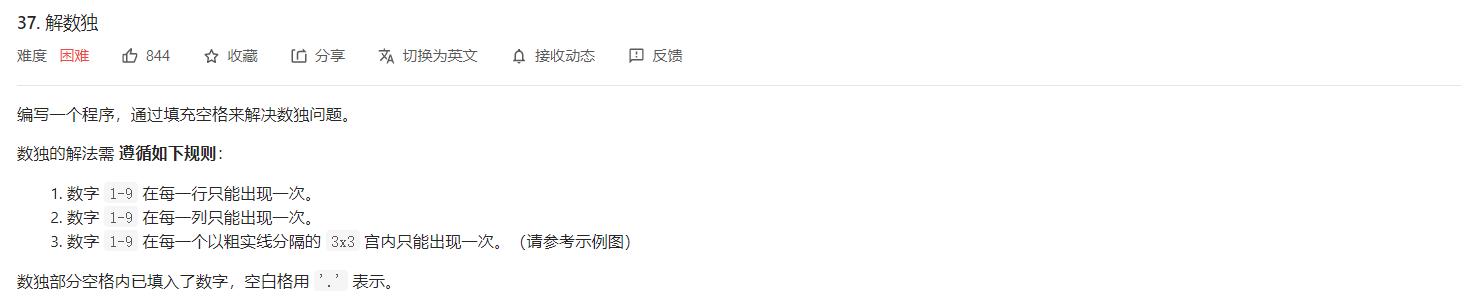
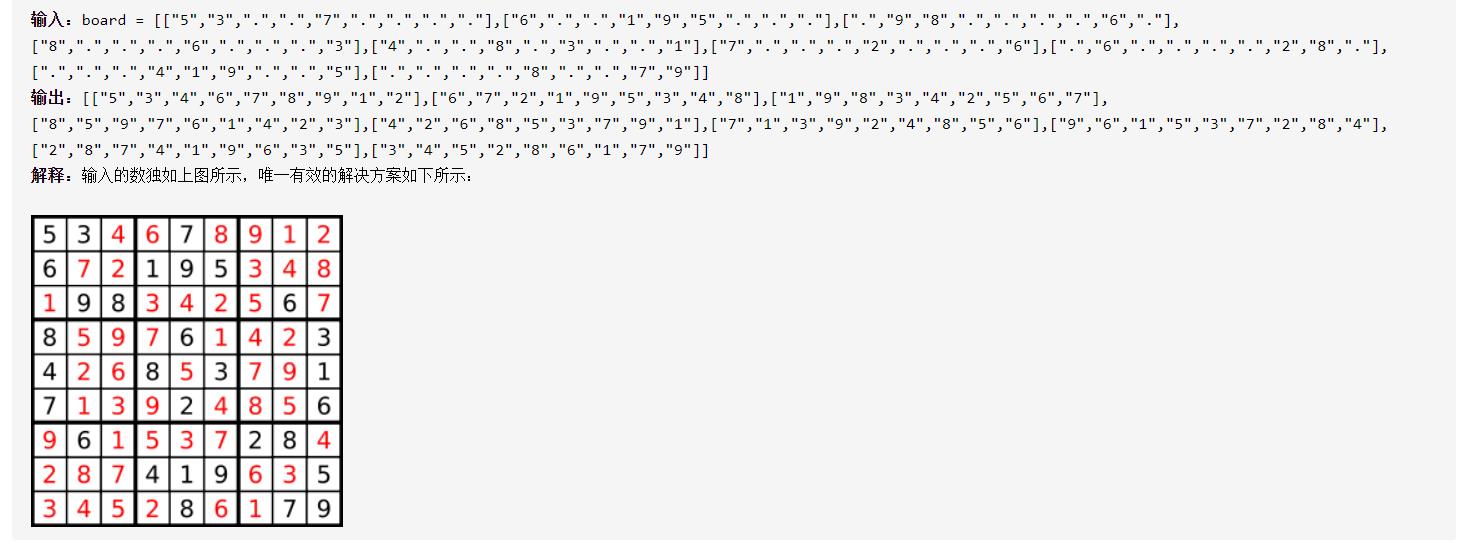
回溯法

这题和八皇后有点相似，不同的是八皇后每行只放一个就可以到下一行继续尝试，而这道题每行都放完没有冲突之后才能到下一行继续尝试，所以判断的逻辑稍微比八皇后多一点，但整体思路没差多少

思路

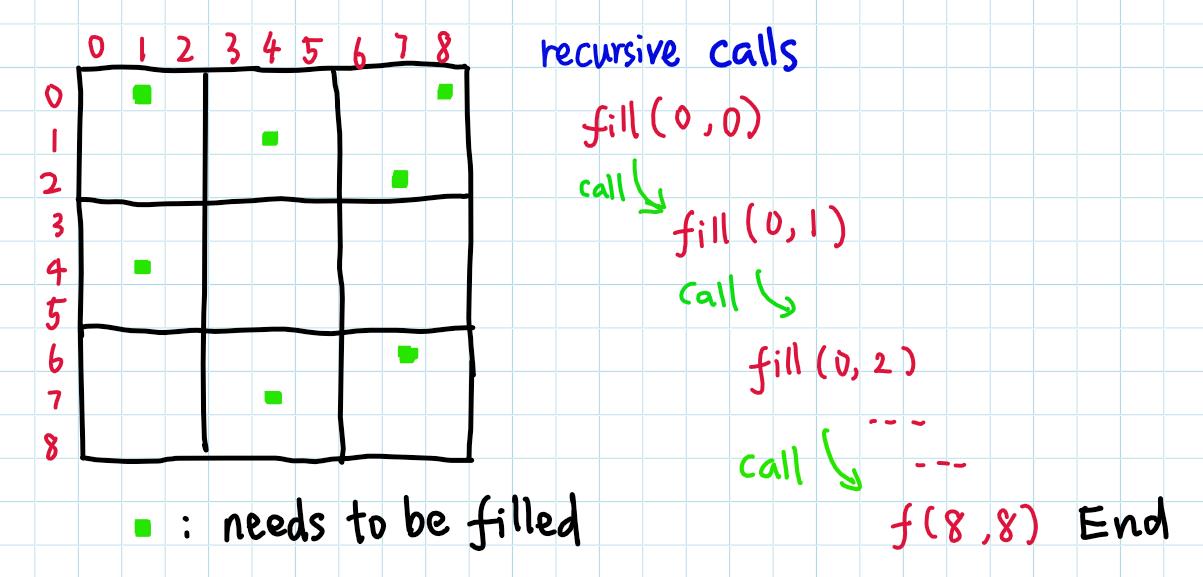
每一个空白格都要选一个数字去填，有多少个空白格，做多少次选择。

可以想到递归，每次递归填当前的格子，选填 i，board 的状态就更新了。

子递归呢？基于填了 i 的新 board，给下一个格子填数。每个递归的子问题，面对一个新 board。

按顺序填下去，如果不是空白格，就继续递归填下一个。

直到递归到最后一个格子，board 填满了，结束递归。

为什么要回溯

每填一个空白格都是尝试，选填一个数，如果没有冲突就填上去，是一种试探。

但如果填 1 到 9 都会冲突，意味着，基于当前 board，这个格子填不了，做不下去。

所以，要撤销当前选择，回到上一格，再改填别的数，再试探。

定义递归函数

子递归是填下一个格子，填不了的话要告知当前递归，撤销当前的选择。

即，根据子递归的结果，判断当前递归的选择是否正确。

递归函数要返回一个Boolean值，定义是：基于当前的 board，给当前的格子board[i][j]填一个数，能否最后生成正确的数独。

能否最后生成正确的数独，是靠递归子调用一个个去填，当填不下去，就撤回上一个选择，尝试别的选择。

这里如何判断填入一个数后是否会冲突，可以参考leetcode 36. 有效的数独，相当于是为本题做的铺垫

这里判断是否冲突使用的是数组法，详情可以去看leetcode 36. 有效的数独

代码:

class Solution {
	int row[9][9] = { 0 };//行标记录是每一行，列标记录可选数字从1---9,如果某个数字出现在了当前行，就把对应的列表值变为1
	int col[9][9] = { 0 };//行标记录是每一列，列标记录可选数字从1---9，如果某个数字出现在了当前列，就把对应的列表值变为1
	int box[9][9] = { 0 };//行标记录是每一个区域，列表记录可选数字1---9,如果某个数字出现在了当前区域，就把当前对应的列表值变为1
public:
	void solveSudoku(vector<vector<char>>& board)
	{
	//将原本表中已经填好的数字进行记录
		for (int i = 0; i < 9; i++)
		{
			for (int j = 0; j < 9; j++)
			{
				if (board[i][j] == '.') continue;
				int cur = board[i][j] - '0';
				row[i][cur - 1] = 1;
				col[j][cur - 1] = 1;
				box[j / 3 + (i / 3) * 3][cur - 1] = 1;
			}
		}
		backTrace(board, 0, 0);
	}
	bool backTrace(vector<vector<char>>& board, int r, int c)
	{
		//如果当前已经遍历完了所有行，所有填完了所有数字并且都有效，返回真
		if (r == board.size()) return true;
		//如果当前列已经遍历完了，从下一行第一个数字开始填起来(如果从下一行第一个数字开始到结尾填的都符合条件，说明整张表填的符合条件)
		if (c == board[0].size()) return backTrace(board, r + 1, 0);
		//如果当前位置已经填了数字，就不需要填了，填下一列的数字
		if (board[r][c] != '.') return backTrace(board, r, c + 1);
		//1----9，九个数字挨个进行抉择，找到一个填入后满足条件的数字
		for (char i = '1'; i <='9'; i++)
		{
			//如果当前位置填入当前数字i，不满足条件，就换下一个数字试探
			if (!isvaild(board, r, c, i - '0')) continue;
			//如果可以，那么填入当前数字，并且记录其在第一行，第几列，第几个区域出现过
			board[r][c] = i;
			row[r][i-'0'-1] = 1;
			col[c][i -'0'- 1] = 1;
			box[c / 3 + (r / 3) * 3][i - '0' - 1] = 1;
			//如果选择了当前数字后，从当前行下一列开始填到结尾，每一个位置都能找到符合的数字，那么返回真
			//虽然当前数字可以填在当前位置，但是会影响后面数字的选择情况，可以这个位置填入该数字后，后面位置无论怎么调试都无法填完，那么就需要更换当前位置选择的数字
			if (backTrace(board, r, c+1)) return true;
			//重新选择当前位置的数字，需要消除之前记录的结果，即恢复原有数据
			board[r][c] = '.';
			row[r][i - '0' - 1] = 0;
			col[c][i - '0' - 1] = 0;
			box[c / 3 + (r / 3) * 3][i - '0' - 1] = 0;
		}
		//如果当前位置九个数字都不满足填入当前位置的条件，说明之前的选择存在问题，需要返回上一层重新选择上一层的数字
		//因为这里数独有且仅有一个解
		return false;
	}
	bool isvaild(vector<vector<char>>& board, int r, int c, int i)
	{
		//判断当前行，当前列，或者当前区域中是否有一个选项发生冲突，发生了，说明当前位置不能填入当前选择的数字
		if (row[r][i - 1]|| col[c][i - 1]|| box[c / 3 + (r / 3) * 3][i - 1]) return false;
		return true;
	}
};

---

位运算

这里建议大家去看大佬的文章解析，因为本人对位运算也不太了解

【解数独】回溯 + 状态压缩（使用 bitset）