论文｜Node2vec算法原理代码实战和在微信朋友圈的应用
Posted Thinkgamer_
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了论文｜Node2vec算法原理代码实战和在微信朋友圈的应用相关的知识，希望对你有一定的参考价值。
1 概述
Node2vec是2016年斯坦福教授 Jure Leskovec、Aditya Grover提出的论文，论文的下载链接为：https://arxiv.org/pdf/1607.00653.pdf。
其本质上是对Deepwalk的延伸，也是属于图神经网络种随机游走模型一类。不了解Deepwalk的可以看上一篇文章：论文｜DeepWalk的算法原理、代码实现和应用说明。
Node2vec在DeepWalk的基础上提出了更加合理的图特征学习方法，提出了用于网络中可伸缩特征学习的半监督算法，使用SGD优化一个自定义的基于图的目标函数，该方法可以最大化的在D维特征空间保留节点的网络领域信息；在随机游走的基础上设计了一种二阶随机游走的过程，相当于对DeepWalk算法的一种扩展，它保留了邻居节点的图特征。
2 算法原理
2.1 学习框架
论文中将网络中的特征学习问题看作是一个极大似然优化问题，设 G = ( V , E ) G=(V,E) G=(V,E)为给定的网络， f : V ⇒ R d f: V \\Rightarrow \\mathbb{R}^d f:V⇒Rd 为节点到特征表征的映射函数，我们的目标是学习一个后续节点的预测任务，这里的 d d d 表示的是节点的表征向量维度， f f f 是一个 ∣ V ∣ ∗ d |V| * d ∣V∣∗d 的矩阵，同时为每个源节点 u ∈ V u \\in V u∈V，定义 N s ( u ) ⊂ V N_s(u) \\subset V Ns(u)⊂V 的网络邻居节点的社区抽样策略。
节点的表征学习目标函数为最大化节点
u
u
u 的网络观测邻域
N
s
(
u
)
N_s(u)
Ns(u)：
m
a
x
f
∑
u
∈
V
l
o
g
P
r
(
N
s
(
u
)
∣
f
(
u
)
)
max \\, f \\sum u \\in V \\, log \\, Pr(N_s(u)|f(u))
maxf∑u∈VlogPr(Ns(u)∣f(u))
但是基于上面的目标函数进行优化，是比较困难的，因此作者做了两点假设：
-
条件独立性假设：即假设结点间相互独立，简单来说就是，对于某一个源结点，其采用到的邻居结点是独立的，采用其中一个邻居结点不会对其他邻居结点造成影响
Pr ( N S ( u ) ∣ f ( u ) ) = ∏ n i ∈ N S ( u ) Pr ( n i ∣ f ( u ) ) \\operatorname{Pr}\\left(N_{S}(u) | f(u)\\right)=\\prod_{n_{i} \\in N_{S}(u)} \\operatorname{Pr}\\left(n_{i} | f(u)\\right) Pr(NS(u)∣f(u))=ni∈NS(u)∏Pr(ni∣f(u)) -
特征空间对称假设：源结点和邻居结点的特征空间有一个对称性影响。简单来说就是，一个源结点和其某一个邻居结点有关系，那么对于这个邻居结点来说，这个源结点也是其邻居结点，影响是相互的
Pr ( n i ∣ f ( u ) ) = exp ( f ( n i ) ⋅ f ( u ) ) ∑ v ∈ V exp ( f ( v ) ⋅ f ( u ) ) \\operatorname{Pr}\\left(n_{i} | f(u)\\right)=\\frac{\\exp \\left(f\\left(n_{i}\\right) \\cdot f(u)\\right)}{\\sum_{v \\in V} \\exp (f(v) \\cdot f(u))} Pr(ni∣f(u))=∑v∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u))
根据以上两个假设，最终目标函数
f
f
f 可以优化为以下形式：
max
f
∑
u
∈
V
[
−
log
Z
u
+
∑
n
i
∈
N
S
(
u
)
f
(
n
i
)
⋅
f
(
u
)
]
\\max {f} \\sum{u \\in V}\\left[-\\log Z_{u}+\\sum_{n_{i} \\in N_{S}(u)} f\\left(n_{i}\\right) \\cdot f(u)\\right]
maxf∑u∈V⎣⎡−logZu+ni∈NS(u)∑f(ni)⋅f(u)⎦⎤
由于归一化因子
Z
u
=
∑
v
∈
V
exp
(
f
(
u
)
⋅
f
(
v
)
)
Z_{u}=\\sum_{v \\in V} \\exp (f(u) \\cdot f(v))
Zu=∑v∈Vexp(f(u)⋅f(v))，对于大型网络来说，计算成本很高，所以采用负采样技术进行优化，在定义特征函数
f
f
f 模型参数上，采用随机梯度上升法对公式最终的目标函数进行优化。
2.2 搜索策略
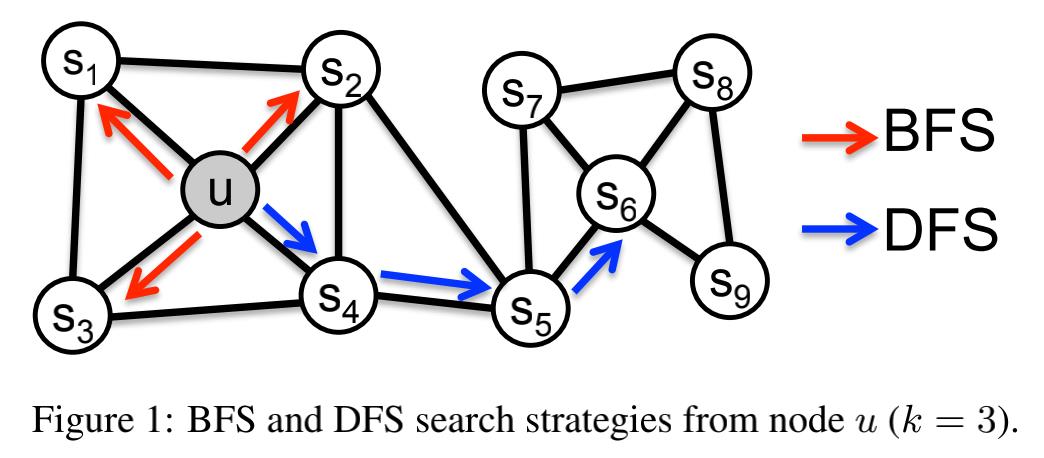
可以将采样源节点邻域问题视为一种网络局部搜索问题，所熟知的无非就是广度优先遍历（BFS）和深度优先遍历（DFS），广度优先更容易采样邻居节点，从而获得每个节点邻居的微观视图，这更容易表示结构的相似性，比如限制一个 k = 3 k=3 k=3 邻居域，节点 u u u 的BFS就会对 s 1 , s 2 , s 3 s1,s2,s3 s1,s2,s3 采样，广度优先遍历采样邻居节点往往重复对此采样，这有利于减少偏差。对深度优先遍历来说，它尽可能深的遍历网络，采样节点更准确的反映了邻居节点的宏观情况，这更容易表示内容相似性，即验证同质性假设，而 u u u 使用DFS就会对 s 4 , s 5 , s 6 s4,s5,s6 s4,s5,s6 进行采样。
2.3 Node2vec
a）随机游走策略
作者根据BFS和DFS的思想设计了一种灵活的带有偏重的随机游走策略，使BFS和DFS能够平滑地融入此策略中。
给定一个源节点
u
u
u，要进行步长为
l
l
l 的随机游走，
c
i
c_i
ci 表示游走序列中第
i
i
i 个节点
c
0
=
u
c_0=u
c0=u，节点
c
i
c_i
ci 由以下分布产生：
p
(
c
i
=
x
∣
c
i
−
1
=
v
)
=
{
π
v
x
Z
,
i
f
(
v
,
x
)
∈
E
0
,
o
t
h
e
r
w
i
s
e
p(c_i = x|c_{i-1}=v) = \\left\\{\\begin{matrix} \\frac {\\pi_{vx}} {Z} , if(v,x) \\in E\\\\ 0, otherwise \\end{matrix}\\right.
p(ci=x∣ci−1=v)={Zπvx,if(v,x)∈E0,otherwise
其中：
- π v x \\pi_{vx} πvx 表示从节点 v v v 到 节点 x x x 的转移概率
- Z Z Z 为归一化常量
定义由参数 p p p 和参数 q q q 引导的二阶随机游走如下：
如图假设随机游走序列由节点
t
t
t 经过了边
(
t
,
v
)
(t,v)
(t,v)，现在要决定节点
v
v
v 的下一步游走方向，所以需要评估出边
(
v
,
x
)
(v,x)
(v,x) 上的转移概率
π
v
x
\\pi_{vx}
π< 以上是关于论文｜Node2vec算法原理代码实战和在微信朋友圈的应用的主要内容，如果未能解决你的问题，请参考以下文章 论文｜SDNE的算法原理代码实现和在阿里凑单场景中的应用说明 论文｜SDNE的算法原理代码实现和在阿里凑单场景中的应用说明 论文｜SDNE的算法原理代码实现和在阿里凑单场景中的应用说明