Codeforces Round #722 (Div. 2) D. Kavi on Pairing Duty(证明和公式图解)

Posted 2021-05-26 issue是fw

LINK

为了方便,定义$(x,y)$表示$x$点和$y$点配对

---

已知第$1$个点和第$x$个点配对,第$2$个点和第$y$个点配对

考虑$y<x$时

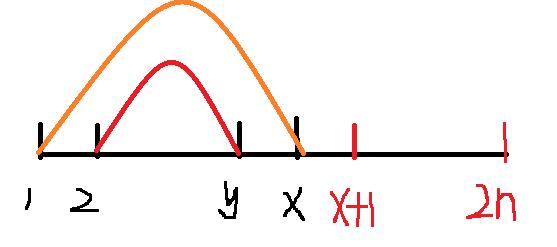
这是不可能的,设和$x+1$这个点配对的点为$z$($z$可能在左边也可能在右边)

显然$(x+1,z)$形成的弧线既不被$(1,x)$包含,也不被$(2,y)$包含

那么就必须满足$abs(x+1-z)=y-2\&\&abs(x+1-z)=x-1$

不可能同时取等号,证毕。

那么现在$y>x$,由于长度必须和$(1,x)$相等,所以$2$只能和$x+1$配对

以此类推,我们知道$3$只能和$x+2$配对,$4$只能和$x+3$配对等等

如图,当$(1,x)$配对时,一个循环节占据的点数为$2\ast (x-1)$

Ⅰ.当$2n\%(2x-2)$为零时,显然可以一直放这个循环节,方案数加一

Ⅱ.否则

①.当$2x-2<2n$时肯定无解,因为最后一个循环节放不满

也就是一定存在长度和$x-1$不等的配对存在,必然会和$(1,x)$产生矛盾

②.当$2x-2>=2n$有解,因为按照上面的放法会变成这个样子

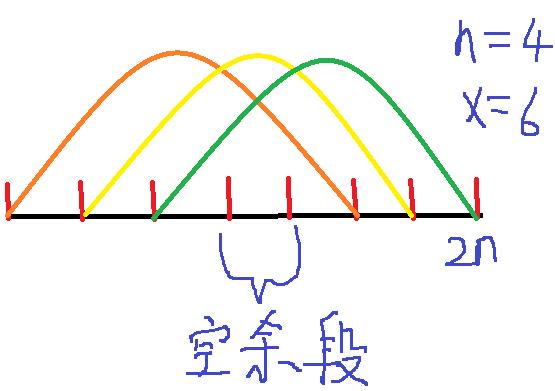
因为此时只有一个循环节,这样放最后中间会空出一部分,点数为$2x-2-2\ast n$

那么其实这个空余段被所有其他配对包含,所以是一个相同的子问题

定义$f[i]$表示$n=i$时的答案

那么Ⅱ部分的答案就是$\sum _{i=1}^{n-1}f[i]$,因为随着$x$的变化这些空余段都可以取到

Ⅰ部分的答案就是$n$的因子个数,记$yinz{i}_i$表示$i$的因子个数

所以得到$$f[i]=yinz{i}_i+\sum _{j=1}^{n-1}f[j]$$

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
const int mod = 998244353;
int f[maxn],yinzi[maxn],sum,n;
signed main()
{
	for(int i=1;i<=1000000;i++)
	for(int j=i;j<=1000000;j+=i)
		yinzi[j]++;
	f[1] = 1, f[2] = 3; sum = 4;
	cin >> n;
	for(int i=3;i<=n;i++)
	{
		f[i] = ( sum+yinzi[i] )%mod;
		sum = ( sum+f[i] )%mod;
	}
	cout << f[n];
}
//	f[0] = 0; f[1] = 1, f[2] = 3; //f[3] = 6;
//	for(int n=3;n<=4;n++)
//	{
//	//	f[n] = 1;
//		for(int i=1;i<=2*n;i++)//第一个段长度为2 
//		{
//			//[i+1.2i]
//			if( 2*n%(2*i)==0 )	f[n] = ( f[n]+1 )%mod;
//			if( i+1<=2*n && 2*i>=2*n )
//			{
//				int ned = 2*n-(i+1);
//				int k = 2*i-2*n;
//				cout << k << endl;
//				f[n] = ( f[n]+f[k>>1] )%mod;
//			}
//		}
//		cout << endl;
//	}
//	cout << f[3] << " " << f[4] << " " << f[100];