[图论]最短路（包括SLF优化spfa的原理)

Posted 2021-05-26 zero_orez6

图的一些简单概念

自环：从某个顶点出发连向自己的边。

环：从某个顶点出发再连到自身的边

重边从一个顶点到另一个顶点有两条边直接相连

图的存储

对于有向图，通常通过邻接矩阵和邻接表两种方法存储，而对于无向图，在没有特殊要求时，通常认为无向边是两条方向相反的有向边

邻接表
通过head数组来记录每个节点第一条边出发的节点在edge.to和edge.next中存储的位置，其中to和val 分别记录每个边的终点和权值，next 记录下一条边在to和val中存储的位置。

struct node{
	int to,next,val;
};
int cnt=0;
void add(int x,int y,int z)//存储一条起点为x，终点为y,权值为z的边 
{
	edge[++cnt].to=y;
	edge[cnt].val=z;
	edge[cnt].next=head[x];
	head[x]=cnt;
}

空间复杂度为$O(n+m)$

邻接矩阵

假设一个图有n个点，那么邻接矩阵就是一个$n\ast n$的二维数组用来存储每个节点与节点的关系

	int a[N][N]
	a[x][y]=z;//存储一条从x到y，权值为z的边

空间复杂度为$O(n^2)$

单源最短路径问题

单源最短路问题（Single Source Short）

dijkstra算法

假设有一个权值全为非负数的图，那么有一种复杂度有保证的单源最短路算法便是$dijkstra$，它的大体流程如下：

1.初始化dis[s]=0（s为源节点）,其余dis值赋值为极大值，

2,从源节点开始，找到v(v为当前节点)所有出边中未被标记的，dis[x]最小的出边。

3.扫描x的所有出边y，如果dis[y]>dis[x]+a[x][y],那么就用dis[x]+a[x][y]更新dis[y]的值，并标记。

4.重复2，3,步骤，直到所有的节点都被标记。

void dij(int s)
{
	memset(dis,10,sizeof(dis));//memset中赋值为10时，数组中并非是10，而是168430090
	dis[s]=0;
	for(int i=1;i<n;i++)
	{
		int x=0;
		for(int j=1;j<=n;j++)
		{
			if(v[j]==0&&(dis[x]>dis[j]||x==0)) x=j;
		}
		v[x]=1;
		for(int j=1;j<=n;j++)
		{
			dis[j]=min(dis[j],dis[x]+a[x][j]);
		}
	}
}

堆优化的dijkstra

因为要遍历所有点及其最小值，所以复杂度为$O(n^2)$，
如何省去找最小值这一过程呢？利用二叉堆对dis数组进行维护，就可以用$O(logn)$的时间求出最小值进行优化了.

void dij(int s)
{
	memset(dis,10,sizeof(dis));
	memset(v,0,sizeof(0)); 
	dis[s]=0;
	v[s]=1;
	q.push(make_pair(0,1));
	while(!q.empty())
	{
		int x=q.top().second;
		q.pop();
		if(v[x]==0)
		{
			v[x]=1;
			for(int i=head[x];i;i=edge[i].next)
			{
				int y=edge[i].to,z=edge[i].val;
				if(d[y]>d[x]+z)
				{
					d[y]=d[x]+z;
					p.push(make_pair(-d[y],y));
				 } 
			}
		}
	}
	
}

时间复杂度$O(mlogn)$

Bellman-ford算法

给定一张有向图，若对于图中某一条边$(x,y,z)$，有$dis[y]<=dis[x]+z$,则称该边为三角形不等式，若所有边都满足三角形不等式，则现在的dis数组就是源节点到所有其他点的最短路。

1.扫描所有边$(x,y,z)$，用dis[x]+z更新dis[y]。

2.重复此操作，直到所有点不能被更新。

spfa算法

1.建立一个队列，起先值有源节点s。
2.取出队头节点x，扫描它的所有出边（x,y,z），若dis[y]>dis[x]+z,用dis[x]+z更新dis[y],并将未被标记的节点y进入队列，并标记
3.重复以上步骤，直到队列为空

void spfa(int s)  
{
	memset(dis,10,sizeof(dis));
	memset(vis,0,sizeof(vis));
    queue<int> q;
    q.push(s);
    vis[s]=1;
    dis[s]=0;
    while(q.size()) 
    {
        int x=q.front();
        vis[x]=0;
        for (int i=link[x];i;i=e[i].next) 
        {
            int y=e[i].y;
            if (dis[y]>dis[x]+e[i].v) 
            {
                dis[y]=dis[x]+e[i].v;
                if (!vis[y])
                {
                    vis[y]=1;
                    q.push(y); 
                }
            }
        }        
		q.pop();
    }
}

时间复杂度为$O(k\ast m)$,其中k为较小的常数 (隔壁dalao说k是这个图的反阿克曼函数)

SLF优化的spfa

思考一下，对于spfa中的每一个点，在行和列相差较大时，且点较密集的图中时，一个点x可能被其他终点为x的边重复入多次，此时spfa的复杂度就会几乎退化为$O(n\ast m)$关于spfa，它死了
我们可以在每次执行入队操作时，判断一下 此节点到源节点的距离$dis[j]$ 和 队首节点到源节点的距离$dis[q.front()]$ 若$dis[j]<dis[q.front]$ 则将此节点放到队首，否则放在队尾，在后面操作这个点就会尽量减少更新次数（因为它已经被尽量小的点更新过）

注意此操作因为要从队首，队尾入队，所以需要用到双端队列，以及在判断时注意队列中是否有元素。

	deque<int> q;//STL双端队列
	if(!q.empty()&&dis[j]<dis[q.front()]) q.push_front(j);//判断队列中是否有元素且dis[j]与dis[q.front()]的大小
	else q.push_back(j);//存入队尾

关于spfa与dijkstra与负环

很多同学不清楚spfa为什么能“跑”负环，而dijkstra不行.

请大家再回忆一下两种算法的循环步骤并对比：

dijkstra
2,从源节点开始，找到v(v为当前节点)所有出边中未被标记的，dis[x]最小的出边。
3.扫描x的所有出边y，如果dis[y]>dis[x]+a[x][y],那么就用dis[x]+a[x][y]更新dis[y]的值，并标记。

spfa
2.取出队头节点x，扫描它的所有出边（x,y,z），若dis[y]>dis[x]+z,用dis[x]+z更新dis[y],并将未被标记的节点y进入队列，并标记

可以发现dijkstra是之间找到了所有出边的最小值并更新（以下简称“锁定”操作），而spfa则是在遍历边的过程中不断地去更新并标记。

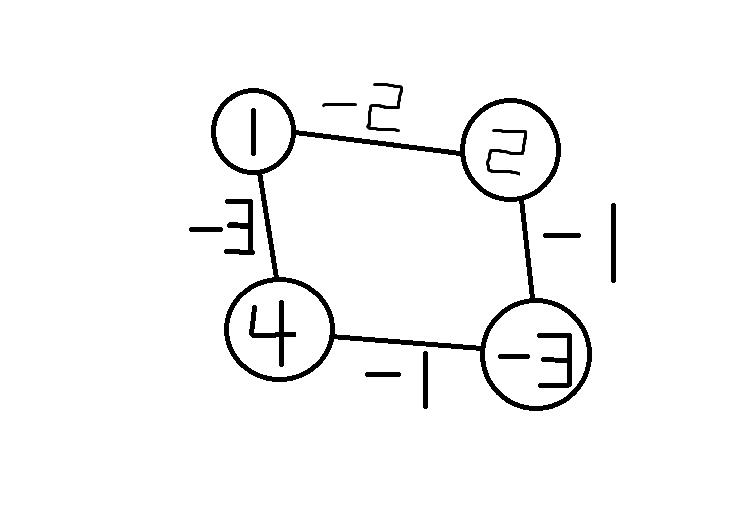
如上图负环所示：

在执行dijkstra的锁定操作时，它会不断地找到当前节点中的最小值并更新，因为有负数的存在每次必定会更新。

而对于spfa的操作时，它在更新之后标记了一下此节点，在后面重新遇到此节点时因为已经标记过，所以不会重复入队。

floyd算法

思想很简单，在一个邻接矩阵中，假设我们有三条边

$a[x_1][y_1]=z_1,a[x_1][k]=z_2,a[k][y_1]=z_3$

其中$z_1>(z_2+z_3)$,那么我们可以毫无疑问地用$z_2+z_3$去更新$a[x_1][y_1]$的值

按照以上思想我们用三层循环遍历所有点$i,j$,以及他们的中间点$k$,并更新。

for(int k=1;k<=n;k++)
{
	for(int i=1,i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
		}
	}
}

注意用邻接矩阵存储，以及将中间点k的枚举放在最外层循环。

传递闭包

当然，基于flord的思想，我们除了处理最小路，还可以用这个算法来 通过传递性推导尽量多的元素之间的关系这种问题被称为传递闭包，用a[i][j]=1表示(i,j)之间有关系，否则无关。

bool a[1086][1086];
int n,m;
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		a[i][i]=1;//自己与自己必定有关系 
	}
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		a[x][y]=a[y][x]=1;//x与y,y与x的关系相同 
	}
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				a[i][j]|=a[i][k]&a[k][
以上是关于[图论]最短路（包括SLF优化spfa的原理)的主要内容，如果未能解决你的问题，请参考以下文章
 
 图论算法 最短路SPFA算法
 OJ记录---图论最短路径问题，DFS，BFS，Dijistra，Dijistra+堆优化，SPFA
 dijkstra最短路算法（堆优化）
 常用最短路优化算法及例题（附模板）——-SPFA和Dijkstra
 最短路算法
 图论-单源最短路-SPFA算法