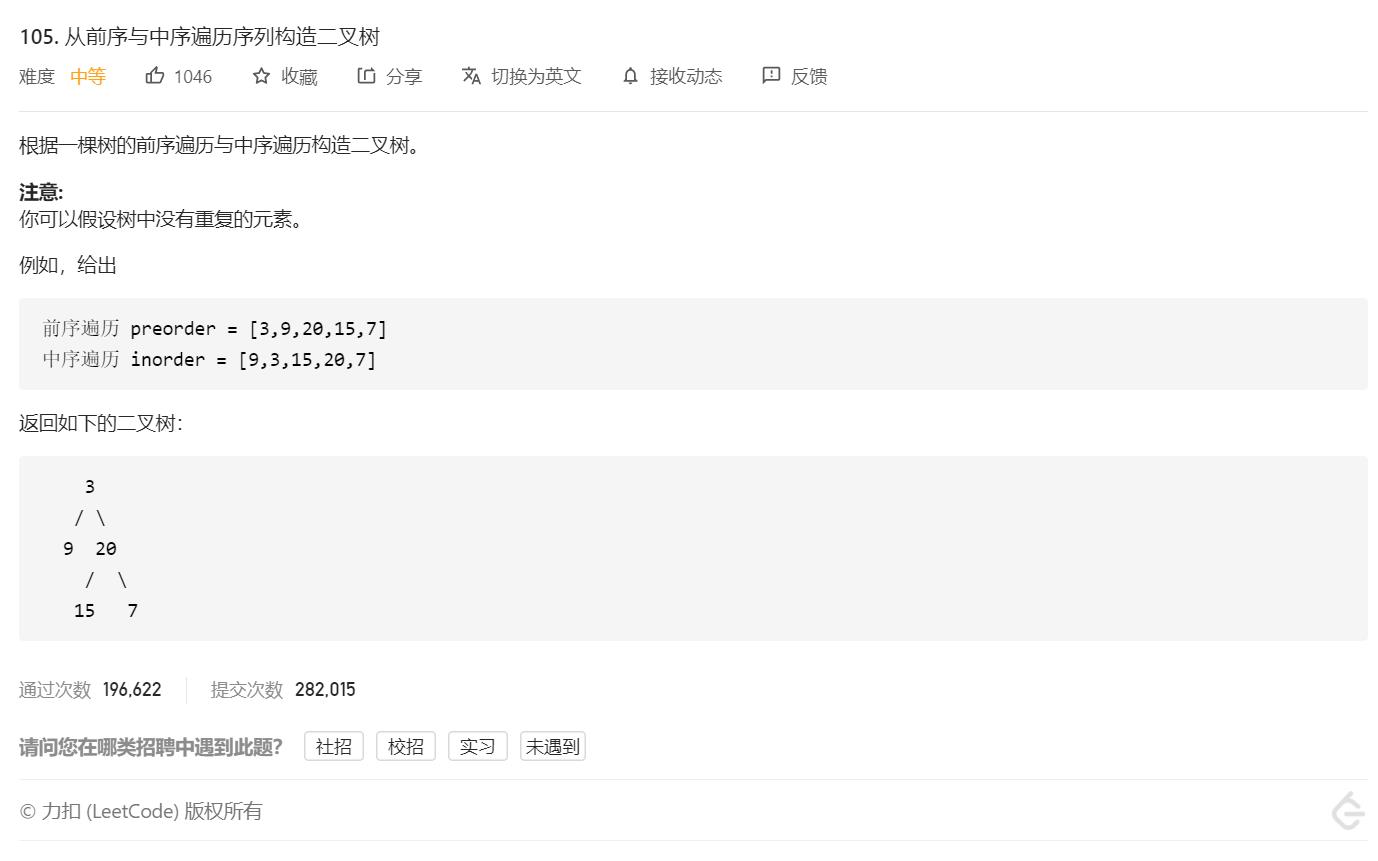
二叉树经典题之从前序和中序遍历构建二叉树

Posted 2021-05-26 快乐江湖

前言：

二叉树刷题是有固定思维的，请移步

README】二叉树刷题框架

从前序和中序遍历构建二叉树

题目

点击跳转：LeetCode

思路

这道题体现的就是分治的思想，我们知道前序遍历啊可以确定一个子树的根节点，而中序遍历可以根据根节点将一颗子树再次分为左右子树，所以只需分解完成依次，后面的过程就是递归过程

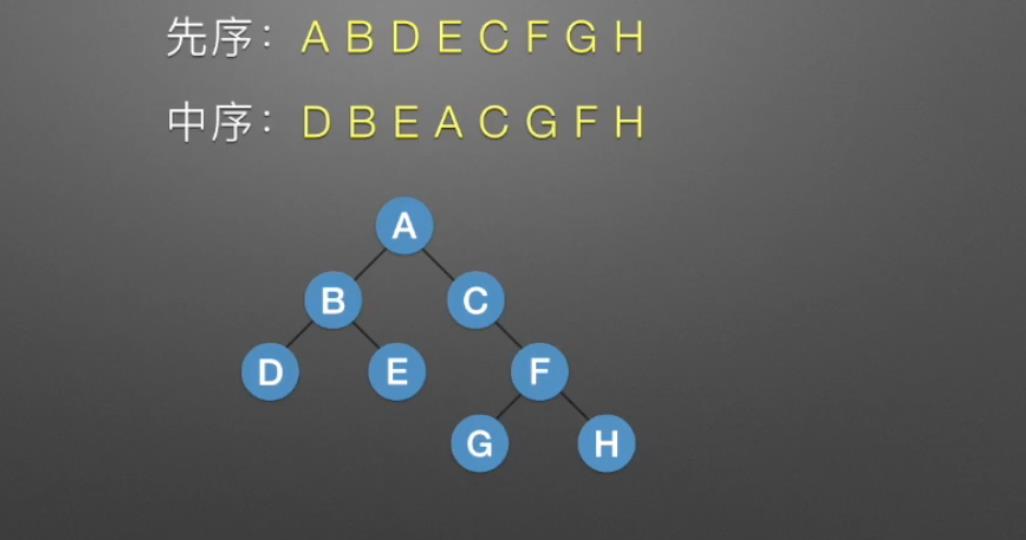
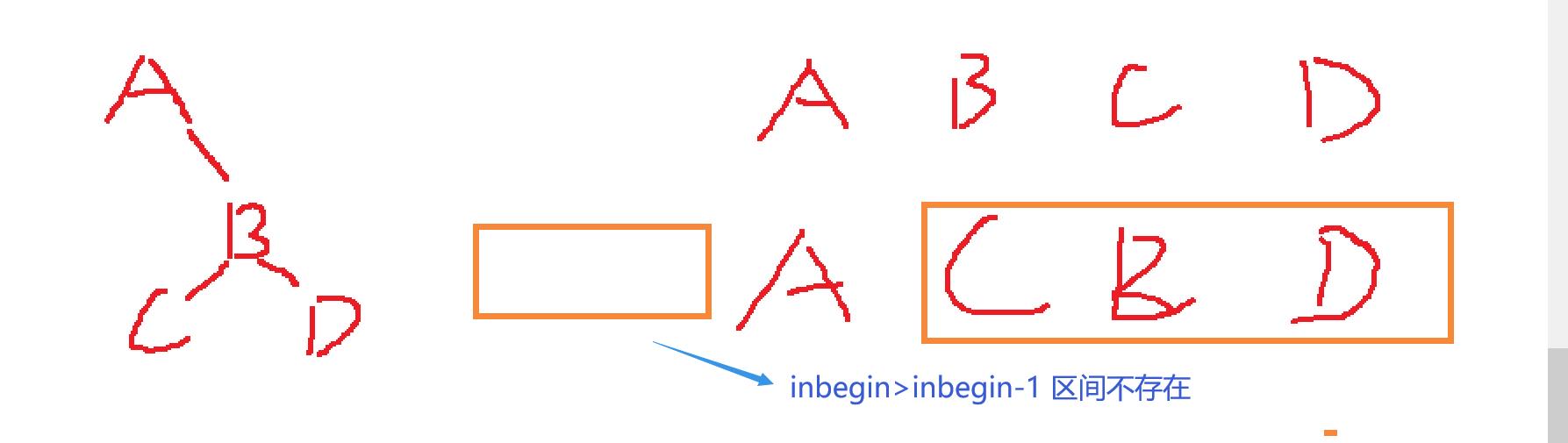
如下，首先根据前序确定这棵树的根节点为A，然后根据中序遍历确定A的左右子树在中序中的范围

下一步又分别确定了左右子树的根节点为B和C

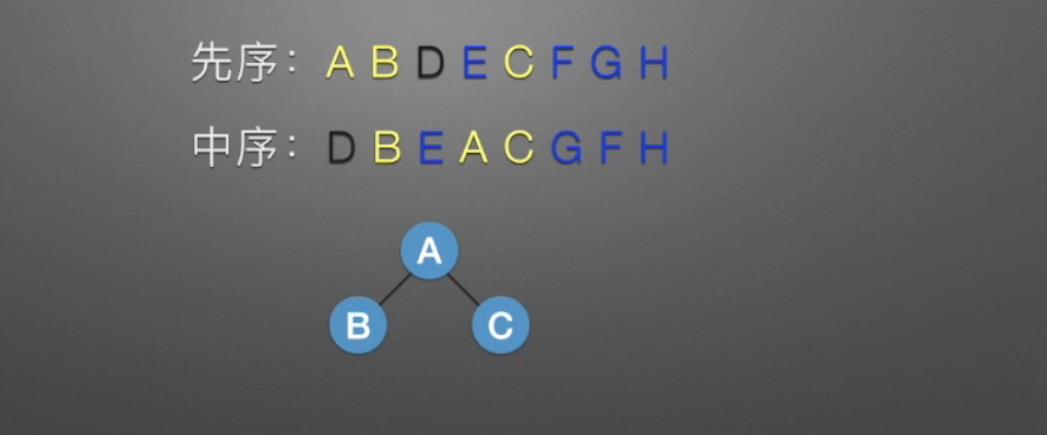
剩下的就是递归过程

代码

class Solution {
public:
    TreeNode* _buildTree(vector<int>& preorder,vector<int>& inorder,int& previ,int inbegin,int inend)
    {
        if(previ >= preorder.size())//前序走完，所有结点构建完成
            return nullptr;
        if(inbegin>inend)//中序区间不存在，也就是该结点不存在左子树
            return nullptr;
        
        int rooti=inbegin;//用rooti保存中序遍历中root的位置
        while(rooti<=inend)//寻找
        {
            if(inorder[rooti]==preorder[previ])
                break;
            else
                rooti++;
                
        }
        TreeNode* root=new TreeNode(preorder[previ]);//依此时前序遍历的第一个值创建一个结点
        ++previ;
        //划分区间，剩余的过程就是递归
        //即[inbegin,rooti-1]root[rooti+1,inend]
        root->left=_buildTree(preorder,inorder,previ,inbegin,rooti-1);
        root->right=_buildTree(preorder,inorder,previ,rooti+1,inend);
        
        return root;
            
        
    }
    
    
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) 
    {
        int previ=0;
        return _buildTree(preorder,inorder,previ,0,inorder.size()-1);
    }
};

注意

上述代码中有一个很重要的判断

if(inbegin>inend)//中序区间不存在，也就是该结点不存在左子树
    return nullptr;

这个判断是为了放置中序遍历区间不存在的情况，如下，下面的树中结点A没有左子树，所以就会导致inbegin > inend