LeetCode 95 不同的二叉搜索树[分治] HERODING的LeetCode之路

Posted 2021-05-25 HERODING23

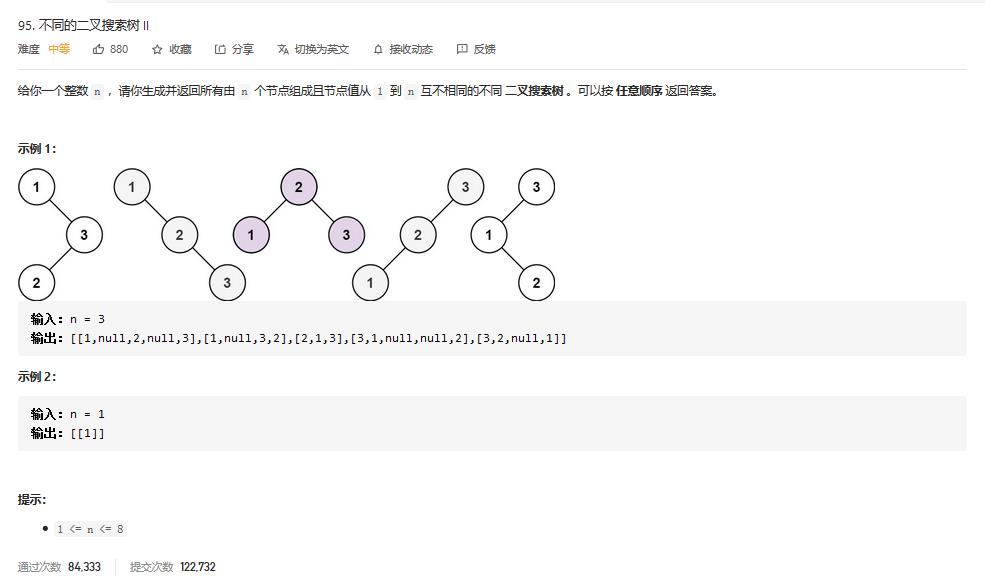解题思路：
一个关于搜索二叉树的分治算法，应该也算是递归的特殊情况了，我们要理清一个思想就是构建好左子树、构建好右子树然后插到root上，其实每个子树也都是这样构建而来的，这也就是分治的真谛，到这一步解题就容易多了。代码注释也很详尽了，代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        vector<TreeNode*> res;
        // 如果为空
        if(n < 1) {
            return res;
        } else {
            return generateSubtrees(1, n);
        }
    }
    vector<TreeNode*> generateSubtrees(int low, int high) {
        vector<TreeNode*> res;
        // 如果大小顺序出问题，不满足搜索二叉树条件
        if(low > high) {
            return { nullptr };
        }
        for(int i = low; i <= high; i ++) {
            // 获取左子树
            vector<TreeNode*> left = generateSubtrees(low, i - 1);
            // 获取右子树
            vector<TreeNode*> right = generateSubtrees(i + 1, high);
            // 左右子树拼接到 root 上
            for(TreeNode* l : left) {
                for(TreeNode* r : right) {
                    TreeNode* root = new TreeNode(i);
                    root -> left = l;
                    root -> right = r;
                    res.push_back(root);
                }
            }
        }
        return res;
    }
};


/*作者：heroding
链接：https://leetcode-cn.com/problems/unique-binary-search-trees-ii/solution/cfen-zhi-xiang-jie-by-heroding-80zh/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。*/