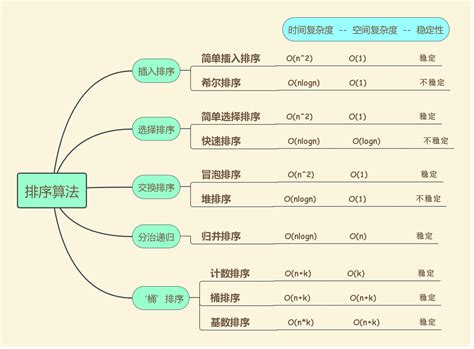
八大排序老忘?视图结合高效写出代码(下)!
Posted 沉默着忍受
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了八大排序老忘?视图结合高效写出代码(下)!相关的知识,希望对你有一定的参考价值。
八大排序老忘?视图结合高效写出代码!
相信很多友友在笔试或者面试的前,如果遇到排序的问题,心中就在想,就是那样那样。可是,一到面对的时候,总是心里一咯噔,沃擦,我怎么说不上来了?本文我会把自己如何快速学习排序的过程分享出来。文章目录
1. 希尔排序(Shell Sort)
1.1 希尔排序是什么?
第一个突破O(n^2)的排序算法;是简单插入排序的改进版;它与插入排序的不同之处在于,它会优先比较距离较远的元素。
希尔排序,也称递减增量排序算法,1959年Shell发明。是插入排序的一种高速而稳定的改进版本。
希尔排序是先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。我们先来看一看希尔的动态演示图:
如果你看不懂动态图,那么下面的静态图可以帮你加深理解
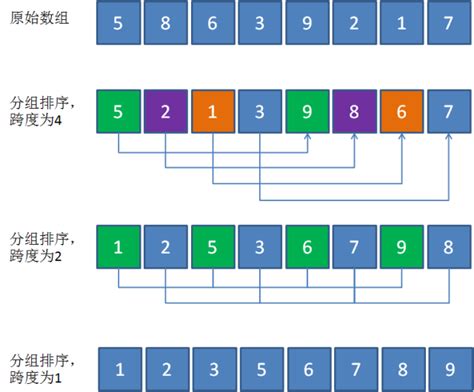
1.2 希尔排序基本思想
将待排序数组按照步长gap进行分组,然后将每组的元素利用直接插入排序的方法进行排序;每次再将gap折半减小,循环上述操作;当gap=1时,利用
直接插入,完成排序, 可以看到步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。一般来说最简单的步长取值是初次取数
组长度的一半为增量,之后每次再减半,直到增量为1
1.3 算法描述
根据上图可以观察得:
①. 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;(一般初次取数组半长,之后每次再减半,直到增量为1)
②. 按增量序列个数k,对序列进行k 趟排序;
③. 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表
来处理,表长度即为整个序列的长度。:
import java.util.Arrays;
/**
* 希尔排序
*
* 1. 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;(一般初次取数组半长,之后每次再减半,直到增量为1)
* 2. 按增量序列个数k,对序列进行k 趟排序;
* 3. 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。
* 仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
* @param arr 待排序数组
*/
public class Deom {
public static void main(String[] args) {
int[] arr = {2,1,6,9,5,4,20,19,11};
shellSort(arr);
}
public static void shellSort(int[] arr){
if(arr==null||arr.length==0){
return;
}
int groud = arr.length/2;
for(;groud>0;groud/=2){
for(int i = 0;i+groud<arr.length;i++){
for(int j = 0;j+groud<arr.length;j+=groud){
if(arr[j]>=arr[j+groud]){
int temp = arr[j];
arr[j] = arr[j+groud];
arr[j+groud] = temp;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
}
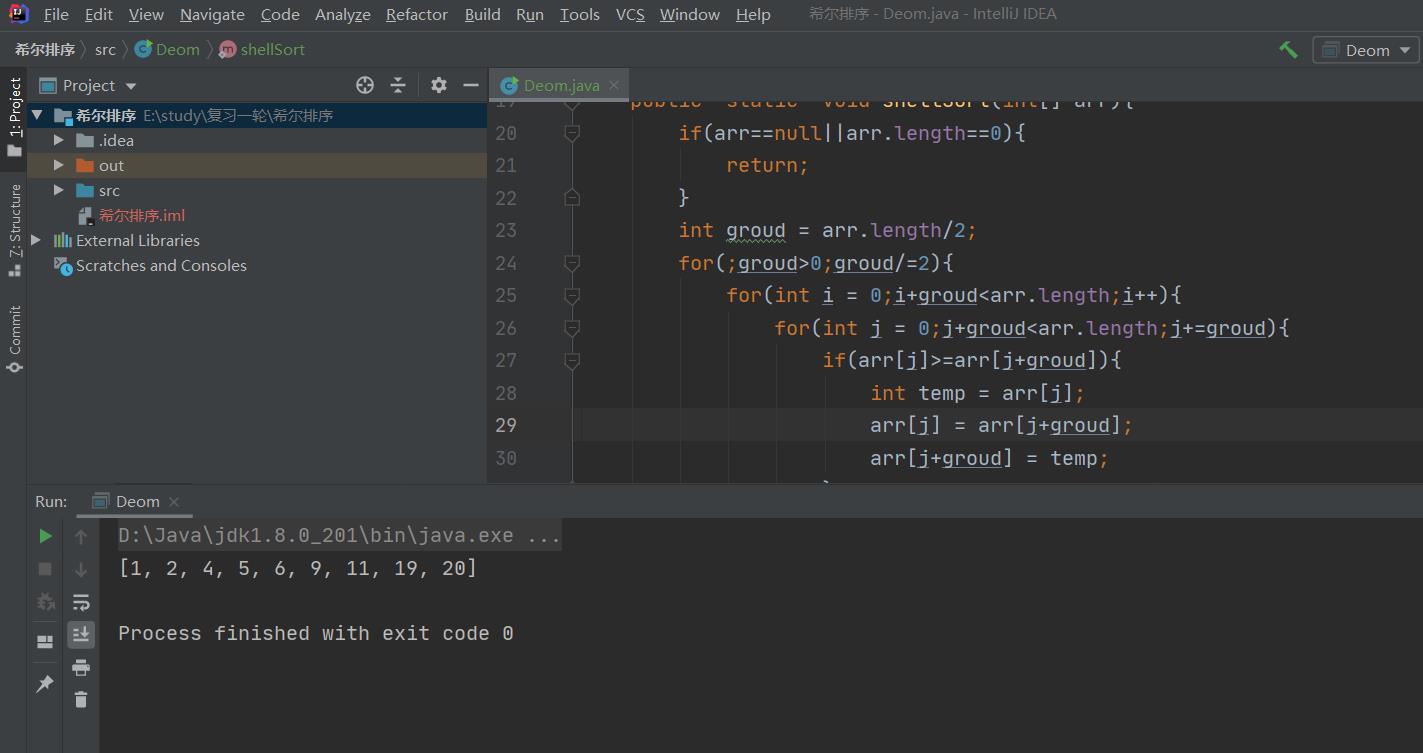
2、堆排序(Heap Sort)
2.1 堆排序是什么?
1991年的计算机先驱奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德(Robert W.Floyd) 和威廉姆斯(J.Williams) 在1964年共同
发明了著名的堆排序算法(Heap Sort).
我们来看一看堆排序的动态演示图:
堆的定义如下:n个元素的序列{k1,k2,···,kn},当且仅当满足下关系时,称之为堆。
ki <= k(2i) 或 ki >= k(2i)
ki <= k(2i+1) ki >= k(2i+1)
把此序列对应的二维数组看成一个完全二叉树。那么堆的含义就是:完全二叉树中任何一个非叶子节点的值均不大于(或不小于)其左,右孩子节点的值。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的,小顶堆的堆顶的关键字是所有关键字中最小的。因此我们可使用大顶堆进行升序排序, 使用小顶堆进行降序排序。
2.2 堆排序的基本思想
如果我们使用大顶堆的特点,那么我们可以将待排序的序列先进行建堆,然后移除堆顶元素,那么该堆顶元素就是序列的最大的数,然后重新建堆,然后再把堆顶的元素移除,直到堆只有一个元素为止(小顶堆原理相同)
2.3 算法描述
①. 先将初始序列K[1…n]建成一个大顶堆, 那么此时第一个元素K1最大, 此堆为初始的无序区.
②. 再将关键字最大的记录K1 (即堆顶, 第一个元素)和无序区的最后一个记录 Kn 交换, 由此得到新的无序区K[1…n-1]和有序区K[n], 且满足K[1…n-1].keys <= K[n].key
③. 交换K1 和 Kn 后, 堆顶可能违反堆性质, 因此需将K[1…n-1]调整为堆. 然后重复步骤②, 直到无序区只有一个元素时停止.
动图效果如下所示:
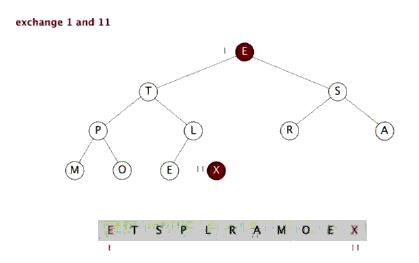
从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆函数,二是反复调用建堆函数以选择出剩余未排元素中最大的数来实现排序的函数。
总结起来就是定义了以下几种操作:
最大堆调整(Max_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
创建最大堆(Build_Max_Heap):将堆所有数据重新排序
堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
对于堆节点的访问:
父节点i的左子节点在位置:(2i+1);
父节点i的右子节点在位置:(2i+2);
子节点i的父节点在位置:floor((i-1)/2);
代码实现:
import java.util.Arrays;
/**
* 堆排序
*
* 1. 先将初始序列K[1..n]建成一个大顶堆, 那么此时第一个元素K1最大, 此堆为初始的无序区.
* 2. 再将关键字最大的记录K1 (即堆顶, 第一个元素)和无序区的最后一个记录 Kn 交换, 由此得到新的无序区K[1..n−1]和有序区K[n], 且满足K[1..n−1].keys⩽K[n].key
* 3. 交换K1 和 Kn 后, 堆顶可能违反堆性质, 因此需将K[1..n−1]调整为堆. 然后重复步骤②, 直到无序区只有一个元素时停止.
* @param arr 待排序数组
*/
public class Demo {
public static void main(String[] args) {
int[] arr = {1,5,4,8,20,15,23,65,45};
heapSort(arr);
}
public static void heapSort(int[] arr){
for(int i = arr.length; i > 0; i--){
max_heapify(arr, i);
int temp = arr[0]; //堆顶元素(第一个元素)与Kn交换
arr[0] = arr[i-1];
arr[i-1] = temp;
}
System.out.println(Arrays.toString(arr));
}
private static void max_heapify(int[] arr, int limit){
if(arr.length <= 0 || arr.length < limit) return;
int parentIdx = limit / 2;
for(; parentIdx >= 0; parentIdx--){
if(parentIdx * 2 >= limit){
continue;
}
int left = parentIdx * 2; //左子节点位置
int right = (left + 1) >= limit ? left : (left + 1); //右子节点位置,如果没有右节点,默认为左节点位置
int maxChildId = arr[left] >= arr[right] ? left : right;
if(arr[maxChildId] > arr[parentIdx]){ //交换父节点与左右子节点中的最大值
int temp = arr[parentIdx];
arr[parentIdx] = arr[maxChildId];
arr[maxChildId] = temp;
}
}
//System.out.println("Max_Heapify: " + Arrays.toString(arr));
}
}
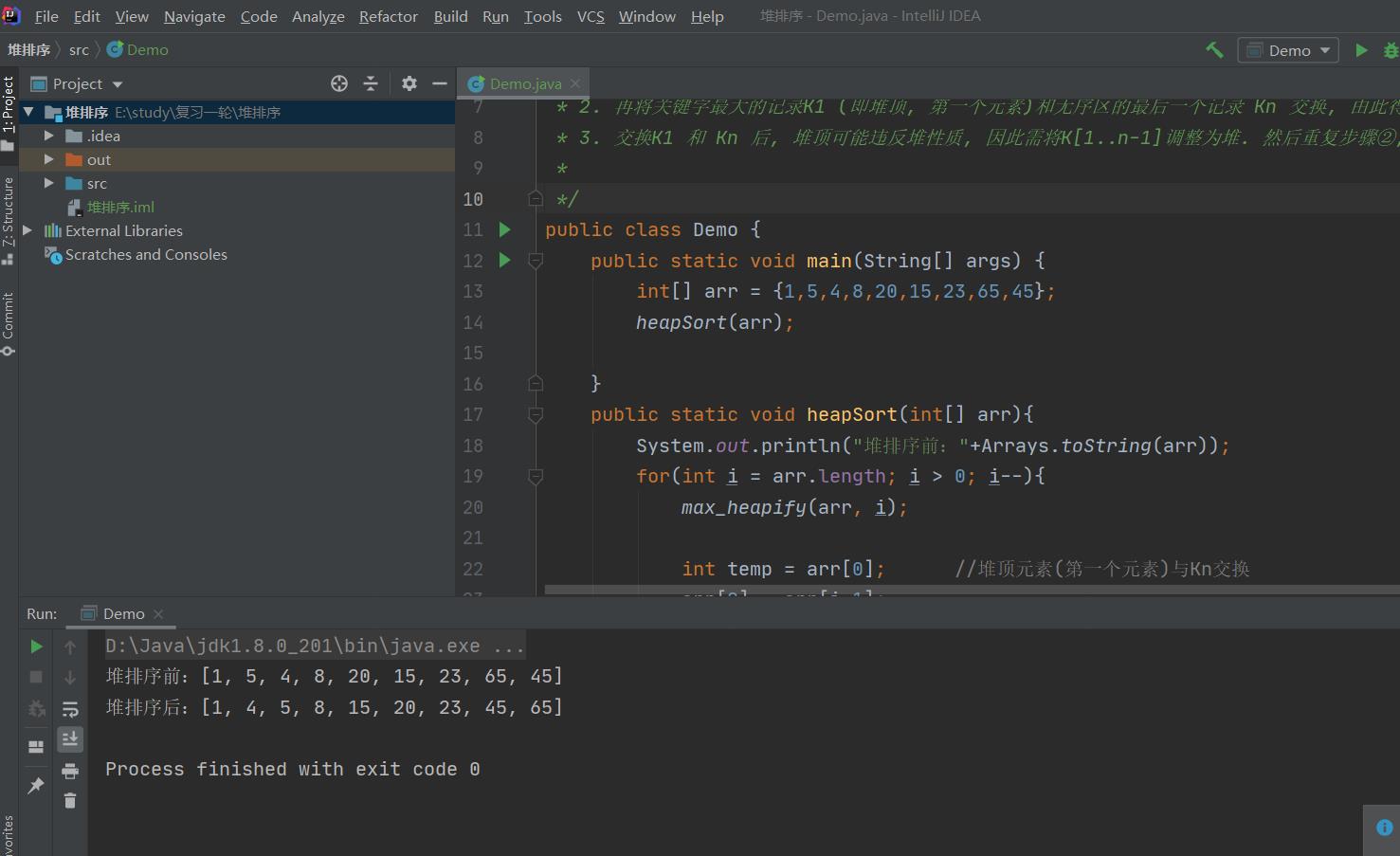
以上,
①. 建立堆的过程, 从length/2 一直处理到0, 时间复杂度为O(n);
②. 调整堆的过程是沿着堆的父子节点进行调整, 执行次数为堆的深度, 时间复杂度为O(lgn);
③. 堆排序的过程由n次第②步完成, 时间复杂度为O(nlgn).
3、归并排序(Merging Sort)
3.1 什么是归并排序?
归并排序是建立在归并操作上的一种有效的排序算法,1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型
的应用,且各层分治递归可以同时进行。
归并排序,顾名思义就是先归并在排序,归并的意思是以固定的长度,将待排序的序列进行分段归并,然后再该分段内将序列排序;
3.2.归并排序的基本思想
归并排序算法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

3.2. 算法描述
我们先来看一看动态演示图来加深理解;
归并排序可通过两种方式实现:
自上而下的递归
自下而上的迭代
一、递归法(假设序列共有n个元素):
①. 将序列每相邻两个数字进行归并操作,形成 floor(n/2)个序列,排序后每个序列包含两个元素;
②. 将上述序列再次归并,形成 floor(n/4)个序列,每个序列包含四个元素;
③. 重复步骤②,直到所有元素排序完毕。
二、迭代法
①. 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
②. 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③. 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④. 重复步骤③直到某一指针到达序列尾
⑤. 将另一序列剩下的所有元素直接复制到合并序列尾

注意:递归和迭代不可同日而语,如果考试,面试遇到的话,请不要混淆。
代码实现:
归并排序其实要做两件事:
分解:将序列每次折半拆分
合并:将划分后的序列段两两排序合并
因此,归并排序实际上就是两个操作,拆分+合并
如何合并?
L[first…mid]为第一段,L[mid+1…last]为第二段,并且两端已经有序,现在我们要将两端合成达到L[first…last]并且也有序。
首先依次从第一段与第二段中取出元素比较,将较小的元素赋值给temp[]
重复执行上一步,当某一段赋值结束,则将另一段剩下的元素赋值给temp[]
此时将temp[]中的元素复制给L[],则得到的L[first…last]有序
如何分解?
在这里,我们采用递归的方法,首先将待排序列分成A,B两组;然后重复对A、B序列
分组;直到分组后组内只有一个元素,此时我们认为组内所有元素有序,则分组结束。
import java.util.Arrays;
public class Demo {
public static void main(String[] args) {
int[] arr = {1,5,3,8,4,6,15,3,24};
System.out.println("归并排序前"+Arrays.toString(arr));
System.out.println("归并排序后"+Arrays.toString(mergeSort(arr)));
}
//将一个序列,拆分成两个序列
public static int[] mergeSort(int[] arr){
if(arr.length<=1) return arr;
int num = arr.length>>1;
int[] leftarr = Arrays.copyOfRange(arr,0,num);
int[] rightarr= Arrays.copyOfRange(arr,num,arr.length);
return mergeTwoArray(mergeSort(leftarr),mergeSort(rightarr));
}
//将两个排好序列的短序列合并为一个序列
public static int[] mergeTwoArray(int[] arr1,int[] arr2){
int i =0;int j =0;int k=0;
int[] result = new int[arr1.length+arr2.length];
while (i< arr1.length&&j<arr2.length){
if(arr1[i]<=arr2[j]){
result[k++]= arr1[i++];
}else {
result[k++]=arr2[j++];
}
}
while (i<arr1.length){
result[k++] = arr1[i++];
}
while (j<arr2.length){
result[k++] = arr2[j++];
}
return result;
}
}
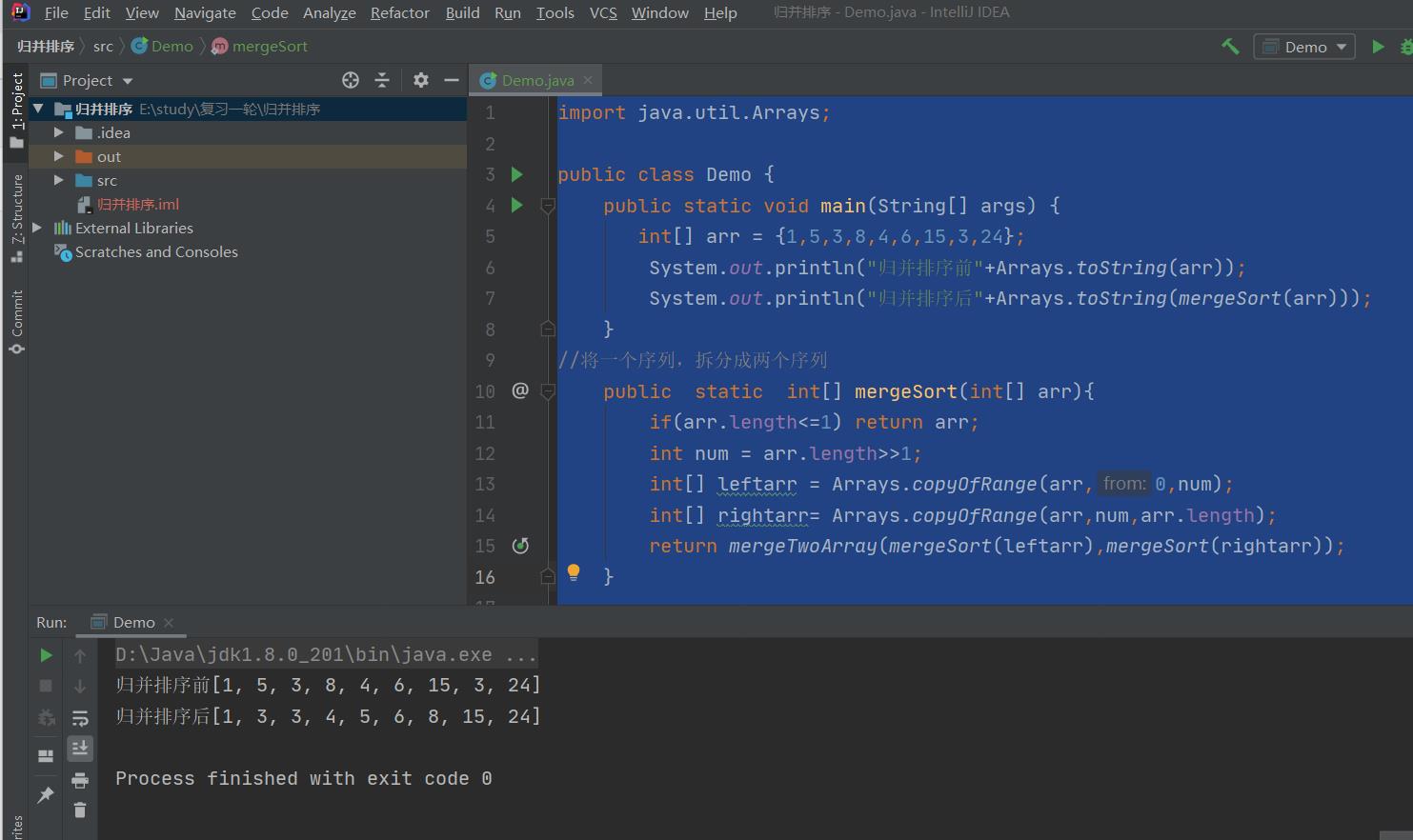
由上, 长度为n的数组, 最终会调用mergeSort函数2n-1次。通过自上而下的递归实现的归并排序, 将存在堆栈溢出的风险。
以下是归并排序算法复杂度:
4、基数排序(Radix Sort)
4.1 什么是基数排序?
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机(Tabulation Machine), 排序器每次只能看到一个列。它是基于元素值的每
个位上的字符来排序的。 对于数字而言就是分别基于个位,十位, 百位或千位等等数字来排序。
基数排序(Radix sort)是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
4.2 基数排序基本思想
它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
基数排序按照优先从高位或低位来排序有两种实现方案:
MSD(Most significant digital) 从最左侧高位开始进行排序。先按k1排序分组, 同一组中记录, 关键码k1相等, 再对各组按k2排序分成子组, 之后, 对后面的关键码继续这样的排序分组, 直到按最次位关键码kd对各子组排序后. 再将各组连接起来, 便得到一个有序序列。MSD方式适用于位数多的序列。
LSD (Least significant digital)从最右侧低位开始进行排序。先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。LSD方式适用于位数少的序列。
动态图片演示:

4.3 算法实现
我们以LSD为例,从最低位开始,具体算法描述如下:
①. 取得数组中的最大数,并取得位数;
②. arr为原始数组,从最低位开始取每个位组成radix数组;
③. 对radix进行计数排序(利用计数排序适用于小范围数的特点);
代码实现:(递归方法)
基数排序:通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序。
分配:我们将L[i]中的元素取出,首先确定其个位上的数字,根据该数字分配到与之序号相同的桶中
收集:当序列中所有的元素都分配到对应的桶中,再按照顺序依次将桶中的元素收集形成新的一个待排序列L[]。对新形成的序列L[]重复执行分配和收集元素中的十位、百位…直到分配完该序列中的最高位,则排序结束
/**
* 基数排序(LSD 从低位开始)
*
* 基数排序适用于:
* (1)数据范围较小,建议在小于1000
* (2)每个数值都要大于等于0
*
* ①. 取得数组中的最大数,并取得位数;
* ②. arr为原始数组,从最低位开始取每个位组成radix数组;
* ③. 对radix进行计数排序(利用计数排序适用于小范围数的特点);
* @param arr 待排序数组
*/
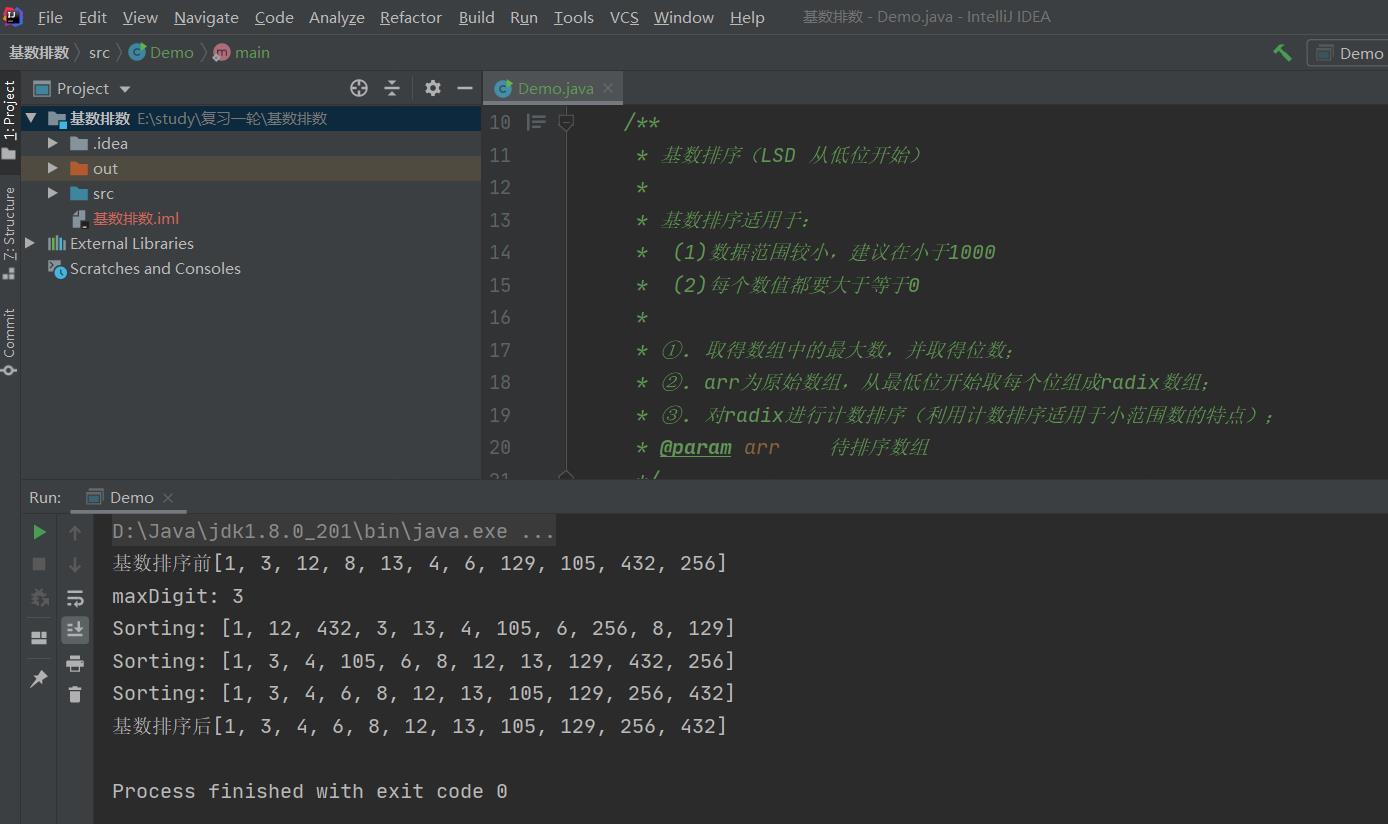
public static void radixSort(int[] arr){
if(arr.length <= 1) return;
//取得数组中的最大数,并取得位数
int max = 0;
for(int i = 0; i < arr.length; i++){
if(max < arr[i]){
max = arr[i];
}
}
int maxDigit = 1;
while(max / 10 > 0){
maxDigit++;
max = max / 10;
}
System.out.println("maxDigit: " + maxDigit);
//申请一个桶空间
int[][] buckets = new int[10][arr.length-1];
int base = 10;
//从低位到高位,对每一位遍历,将所有元素分配到桶中
for(int i = 0; i < maxDigit; i++){
int[] bktLen = new int[10]; //存储各个桶中存储元素的数量
//分配:将所有元素分配到桶中
for(int j = 0; j < arr.length; j++){
int whichBucket = (arr[j] % base) / (base / 10);
buckets[whichBucket][bktLen[whichBucket]] = arr[j];
bktLen[whichBucket]++;
}
//收集:将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞
int k = 0;
for(int b = 0; b < buckets.length; b++){
for(int p = 0; p < bktLen[b]; p++){
arr[k++] = buckets[b][p];
}
}
System.out.println("Sorting: " + Arrays.toString(arr));
base *= 10;
}
}
总结
小胡呕心沥血写了四个排序的图解,排序的时间复杂度和稳定性我会单独写一篇文章,今天我们主要掌握算法,别忘了收藏,转发,评论偶!以上是关于八大排序老忘?视图结合高效写出代码(下)!的主要内容,如果未能解决你的问题,请参考以下文章