深度学习入门与实战

Posted 2021-05-25 gonghaiyu

数学基础

线性代数

深度学习背后的核心是标量、向量、矩阵和张量这 4 种数据结构，通过使用这些数据结构，以编程的方式解决所有基本的线性代数问题。

标量

标量，实际上就是一个单独的数。

向量及其运算

一个向量表示一组有序排列，并可以通过索引获取其中对应位置的数值。一般情况下，我们会选择 NumPy 对向量进行表示和计算。NumPy 是 Python 的一个扩展程序库，能够很好地支持数组、向量、矩阵的运算。它的官网地址为：https://numpy.org/。

向量和标量的计算

标量在跟向量进行加减乘除的时候，实际上与向量中的每一个数字都同步进行了计算。

向量之间的加减操作

向量之间的加减操作是各自对应位置的加减操作。因为 Python 的数组相加是列表的拼接操作，所以在 Python 中，向量的计算不能使用 Python 数组的计算方法。

向量之间的乘法操作

向量之间的乘法操作主要分为点乘（内积）、叉乘（外积）和对应项相乘。

1. 点乘

向量的点乘，也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。给定两个向量：a=[a1, a2…an]和 b=[b1,b2…bn]，则 a 和 b 的点乘计算方式为 a·b = a1b1+a2b2+…+anbn。

2. 叉乘
   向量的叉乘，也叫向量的外积、向量积。叉乘的运算结果是一个向量而不是一个标量。

3. 对应项相乘
   对应项相乘，顾名思义，就是两个向量对应的位置相乘，得到的结果还是原来的形状。

矩阵及其运算

矩阵一般是一个 m 行 n 列的矩形阵列。

矩阵的加减法

矩阵的加减法操作跟向量类似，也是对应位置进行相加减。如图所示，红色和绿色的框分别代表了不同位置数字的计算过程。

矩阵的乘运算

第一种是两个形状一样的矩阵的对应位置分别相乘。

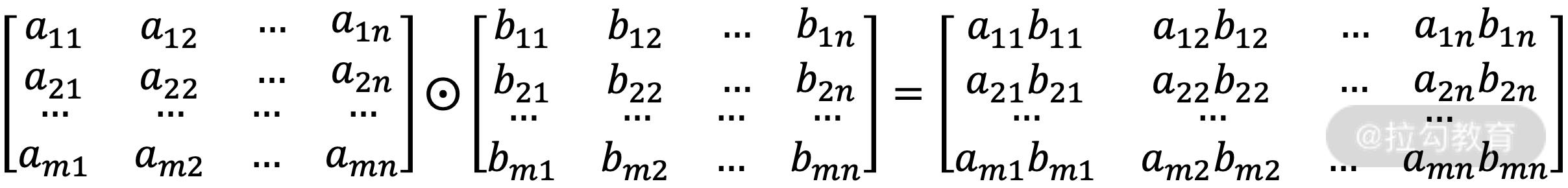
第二种则是矩阵乘法。设 a 为 m 行 p 列的矩阵，b 为 p 行 n 列的矩阵，相乘的结果为一个 m 行 n 列的新矩阵，其中第 i 行第 j 列（1≤i≤m,1≤j≤n）的元素为：

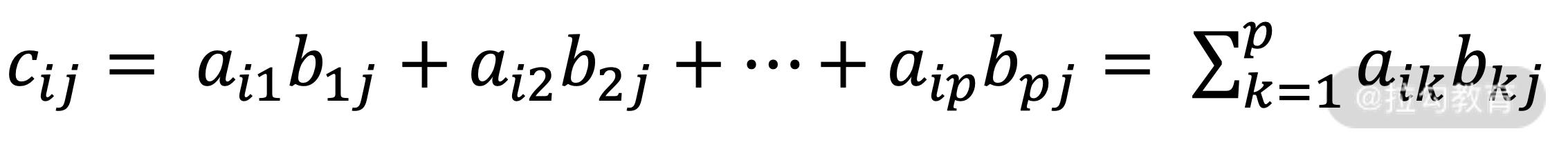
范数

范数是一种距离的表示，或者说向量的长度。
常见的范数有 L0 范数、L1 范数和 L2 范数。

L0范数

L0 范数指这个向量中非 0 元素的个数。我们可以通过 L0 范数减少非 0 元素的个数，从而减少参与决策的特征，减少参数。这样一来，自然模型就运算得更快，模型的体积也更小了。

L1 范数

L1 范数指的是向量中所有元素的绝对值之和，它是一种距离的表示（曼哈顿距离），也被称为稀疏规则算子，公式如下：

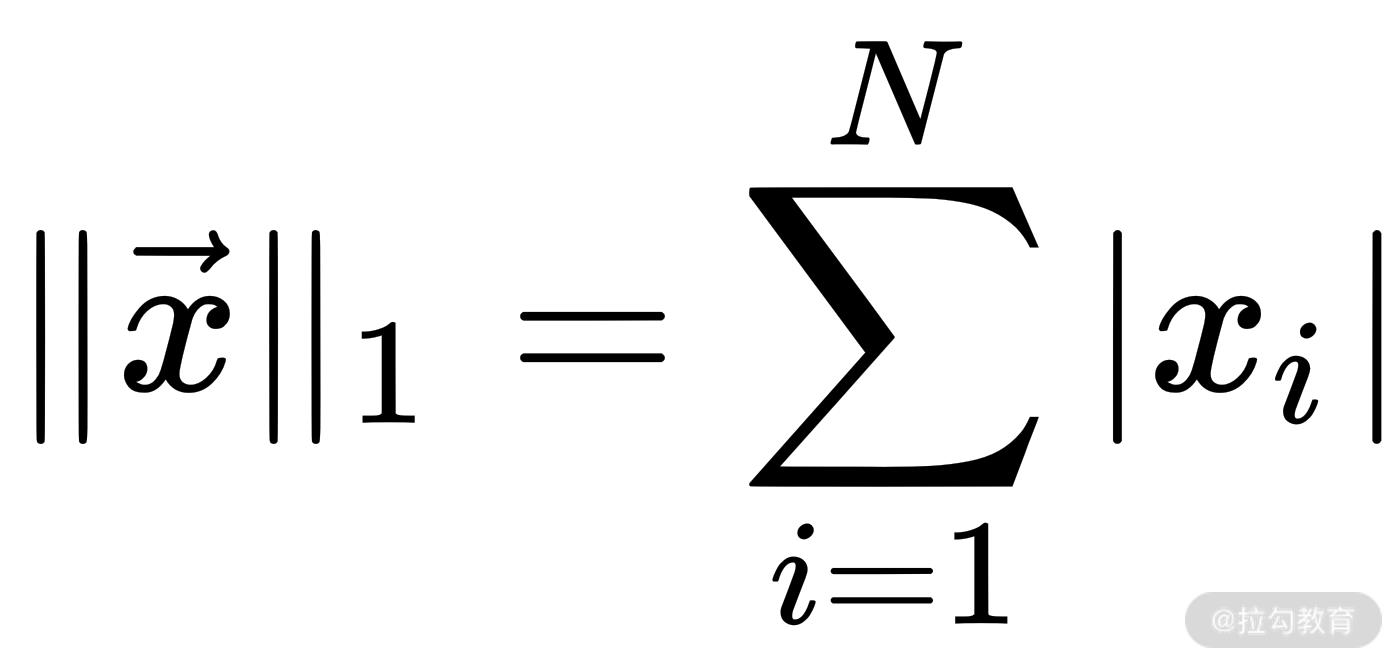
L0 范数和 L1 范数都能实现权值稀疏。但 L1 范数是 L0 范数的最优凸近似，它比 L0 范数有着更好的优化求解的特性，所以被更广泛地使用。

我们为什么要实现权值稀疏呢？

在设计模型的过程中，我们有时会使用到大量的特征（例如在推荐系统中，特征维度都是上亿的），每个特征都会从不同的角度体现问题的不同信息。这些特征经过某些方式的组合、变换、映射之后，会按照不同的权重得到最终的结果。

但有时候，有一部分特征对于最后结果的贡献非常小，甚至近乎零。这些用处不大的特征，我们希望能够将其舍弃，以更方便模型做出决策。这就是权值稀疏的意义。

L2 范数

L2，也有叫它“岭回归”和“权值衰减”的。我们首先来看它的定义：L2 范数是向量中所有元素的平方和的平方根。

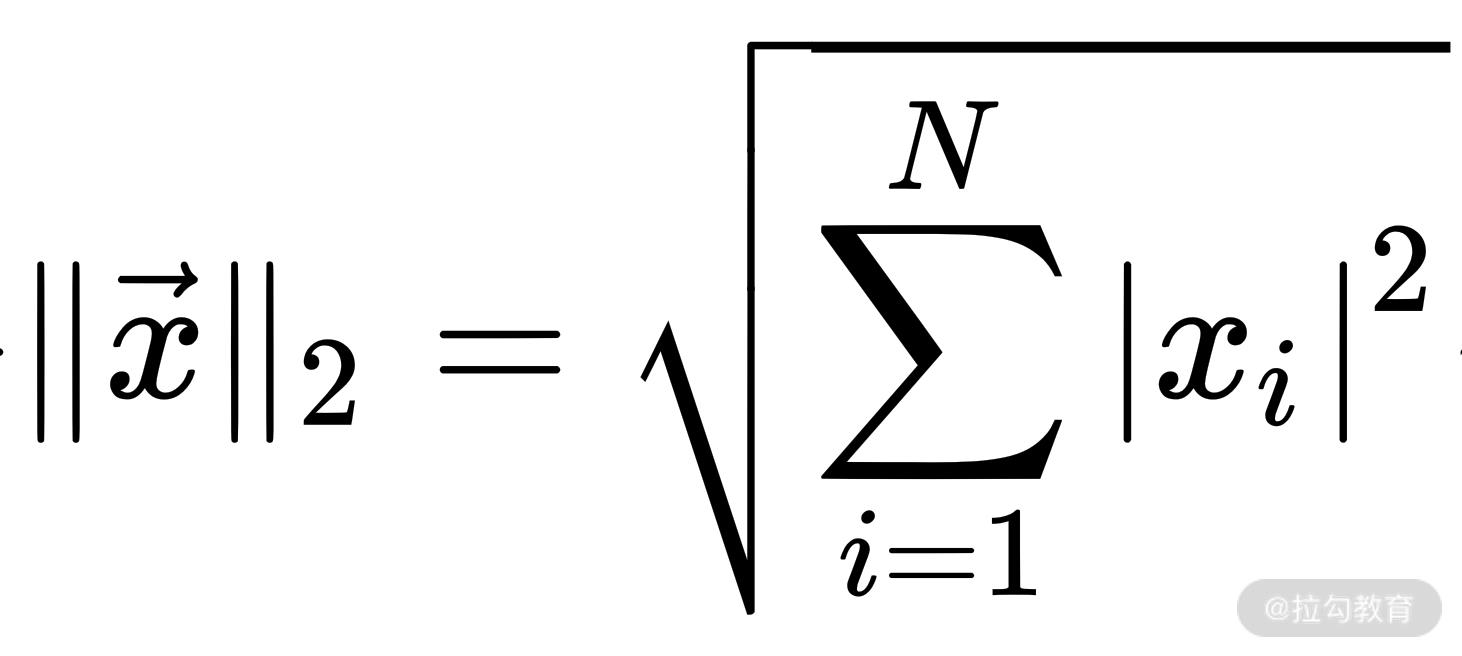
L2 也代表一种距离，即欧式距离。

我们刚才提到 L0 和 L1 可以起到权值稀疏的作用，L2 也有它的作用，那就是防止过拟合。我们先来看什么是过拟合，再来了解为什么 L2 可以减少过拟合。用通俗的话来讲就是模型的应试能力很强，实际应用表现就很差。这种情况就是过拟合。

一个简单的例子，y=10x1+1000x2。x2 取值 1 和 3，最终会导致 y 差了 2000。x2 稍微一变，结果就差别很大了。更进一步，x1 的权重就低了很多，x1 的变化对 y 的结果影响小，模型的适应性就很差了。所以，我们可以得出一个结论：越小的参数，模型就越简单，越简单的模型，就越不容易过拟合。

微积分部分概念

微积分是现代数学的核心基础知识。分别是导数、偏导数和梯度。我们先从导数开始。

导数

导数实际上就是咱们平时说的斜率。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。不光函数有导数，导数也有导数。代表函数在 x 处斜率（导数）的变化率我们称之为二阶导数。由此类推，还有高阶导数等。

偏导数

在实际应用中，很多函数都有多个变量。为了方便分析不同变量与函数的关系，为单个变量求导是很有必要的。这个时候，我们需要让其他变量不变，只有某一个变量发生变化，这种情况下的求导我们称之为“偏导数”。

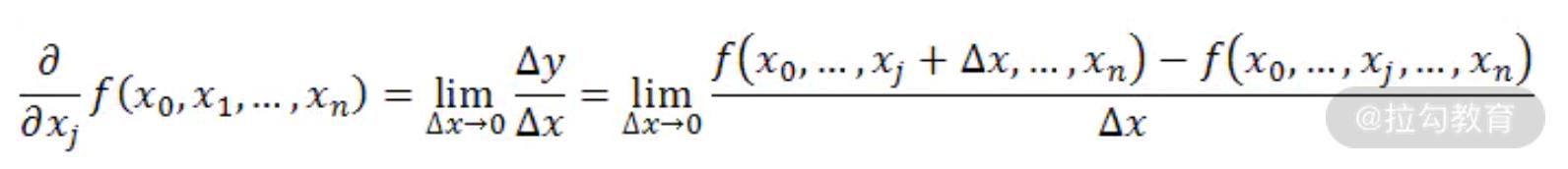
刚才说过，导数就是函数在某个点上的斜率。如果我们把坐标系从二维变成三维，甚至更多维时，偏导数就不难理解了：它实际上是函数在不同方向（坐标轴）上的变化率。就好比爬山，任意一个位置，都会有东西方向和南北方向的坡度（斜率）。

梯度

在机器学习中，梯度是一个出现频率极高的词语，模型的设计、训练、优化等过程中，梯度都是一个核心概念。函数的所有偏导数构成的向量就叫作梯度。我们用∇f 表示，公式化的形式为：

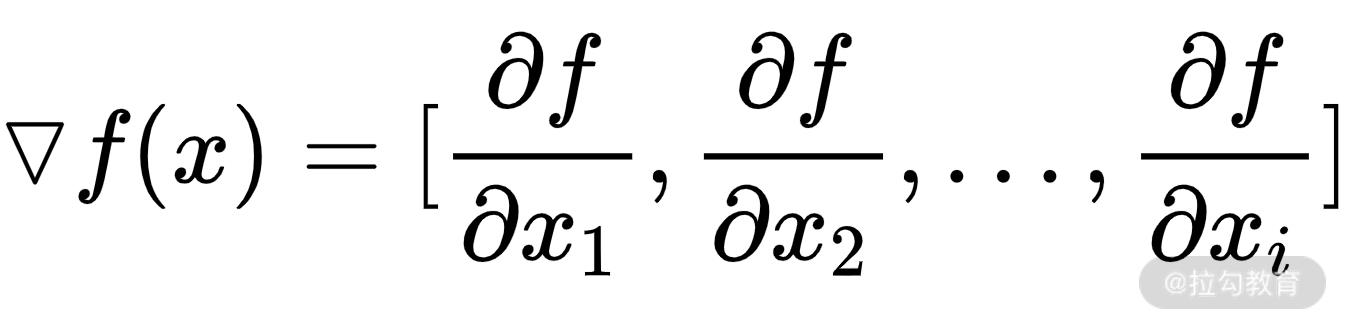
一定要注意，梯度是一个向量。同时，梯度向量的方向即为函数值增长最快的方向。在后续的课时中，我将会介绍损失函数、反向传播、优化方法等内容，它们都离不开梯度。

信息论部分知识点

信息论，在深度学习中是一个非常重要的概念，它集成了微积分、概率论和统计学中很多的概念和想法。它的应用场景非常多，像损失函数中的交叉熵损失、机器学习中构建决策树使用到的信息增益、NLP 和语音算法中的维特比算法等。

提到信息论，就不得不从最基础的熵的定义开始。

熵

熵，也称信息熵。

假定我们有一枚标准的硬币，每次投掷，得到正面和反面的概率都是 1/2，不确定性非常大。假如我们在硬币上做点手脚，在正面加点重量，那么每次投掷的概率就发生了变化，正面朝上的概率就比原来大了，比如此时变成了 2/3，这种正反面的不确定性就减少了。

对于每一个事件（情况）的发生，都有一个信息量的度量，它的公式为：

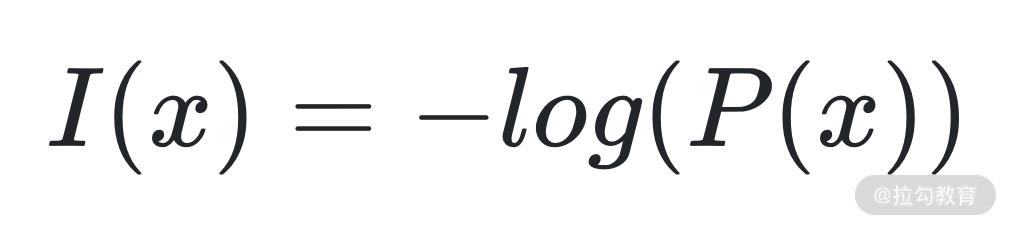
其中 P(x) 是 x 发生的概率。

以投掷硬币来说，投硬币是有正反两种不确定性（概率为 pi）的。我们将这两种不确定性的总量进行量化，就成了: -log(P(正面)) - log(P(反面))。

当我们把投掷硬币推广到更广义的场景下，就得到了熵的定义公式，如下：

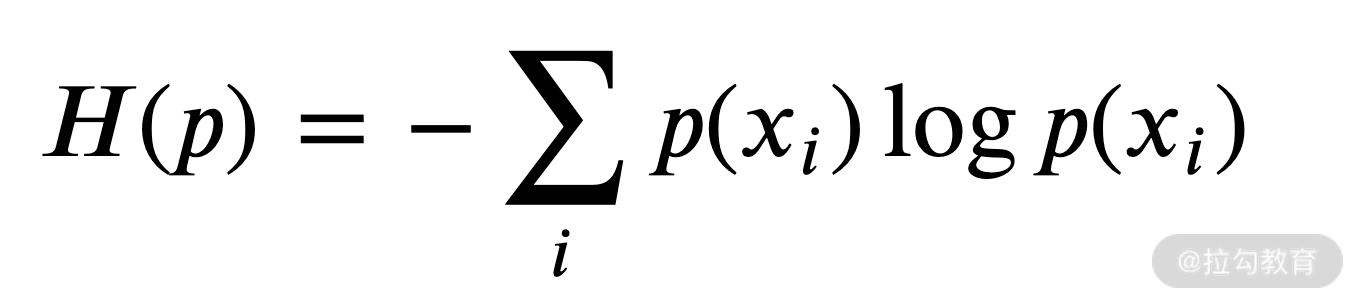
这个公示就是信息熵的公式，其中 p(xi)就是各个可能事件发生的概率。通过公示可以看出，熵越大，不确定性越大。

KL 散度

KL 散度，也称为相对熵，它衡量了两个分布之间的差异。我们来看它的公式：

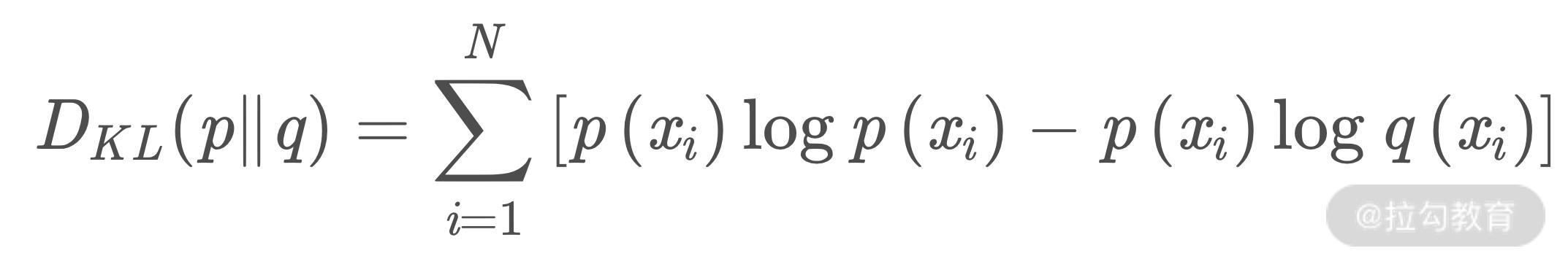
上面的 p(xi) 为真实事件的概率分布，q(xi) 为理论拟合出来的该事件的概率分布。因此该公式字面上的含义就是真实事件的信息熵，同理论拟合的事件的信息量与真实事件的概率的乘积的差的累加。

这句话非常的长，我们拆开来看，真实事件的信息熵就是 p(xi) log p(xi)，理论拟合的事件的信息量就是 log q(xi)，真实事件的概率就是 p(xi)。

在模型优化、数据分析和统计等场合下，我们就可以使用 KL 散度衡量我们选择的近似分布与数据原分布有多大差异。当拟合事件和真实事件一致的时候 KL 散度就成了 0，不一样的时候就大于 0。

交叉熵

交叉熵也衡量了两个分布之间的差异，但是与 KL 散度的区别在于，交叉熵代表用拟合分布来表示实际分布的困难程度，其公式如下：

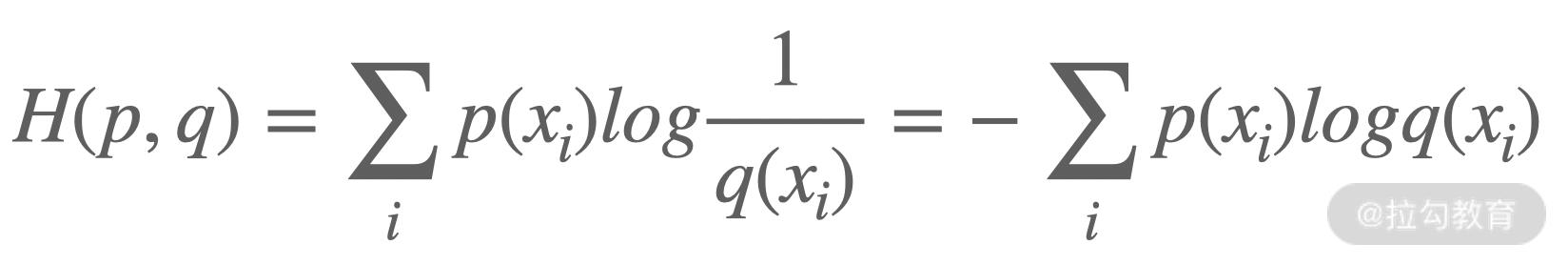
三种度量方式的公式，如果我们放在一起看，就发现其中的关联，如下所示：

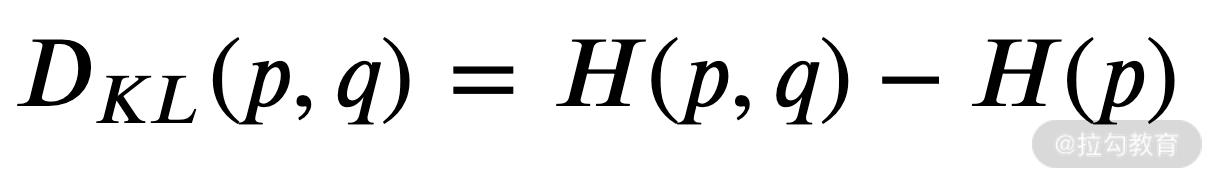
深度学习的起源

神经元与感知机

神经元

深度学习的算法，基本都是一层一层的复杂的网络结构。就像刚才讲到的，会模仿人脑处理信息一样。我们把这种网络称之为“人工神经网络”，它是卷积神经网络的基础。

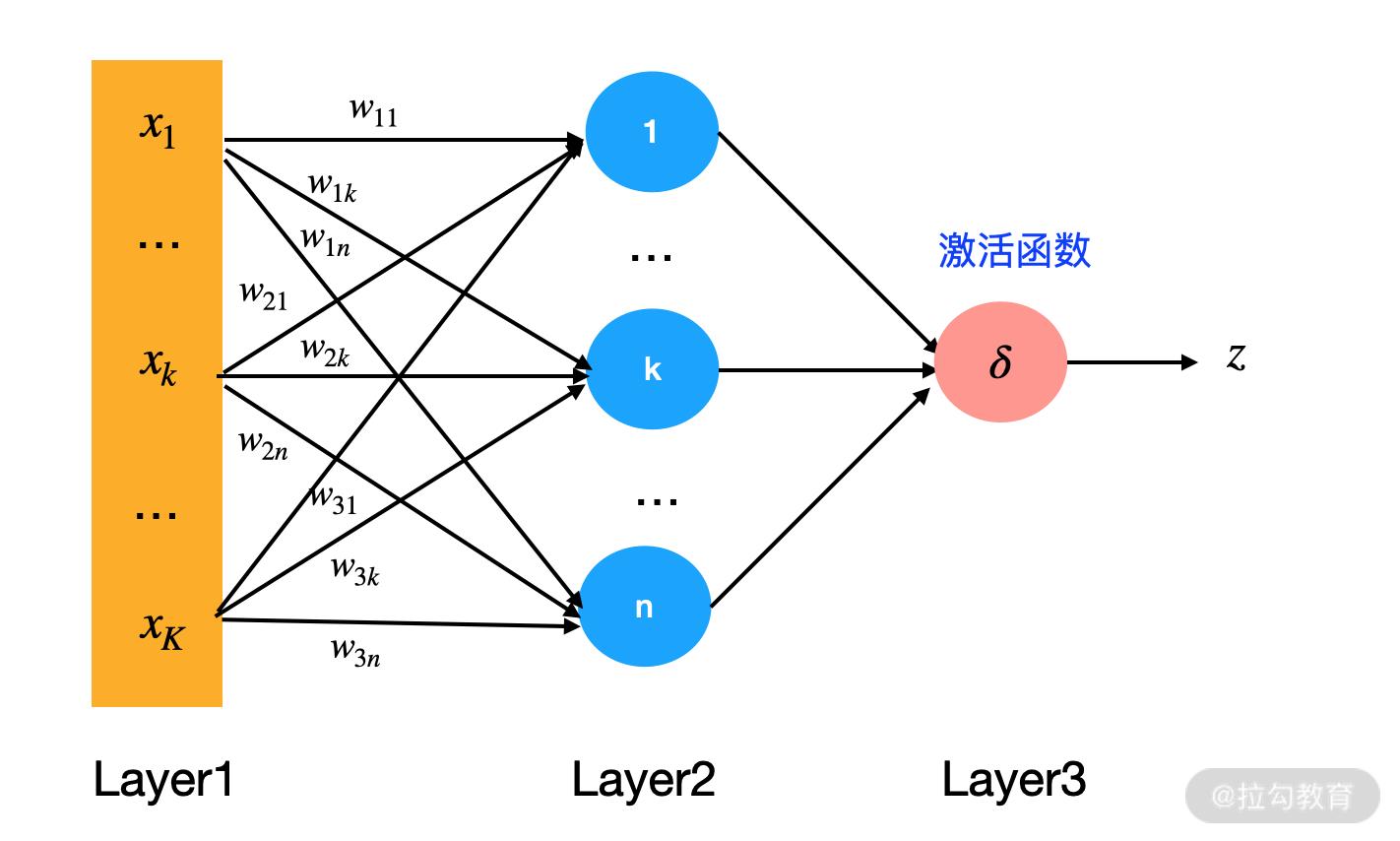
人工神经网络是由一个个神经元组成的，神经元是人工神经网络中最基础的计算单元。神经元接受前一层的输入，经过处理会有一个输出。就像下面这张图一样，接受输入（x1, x2, …），然后输出 z：

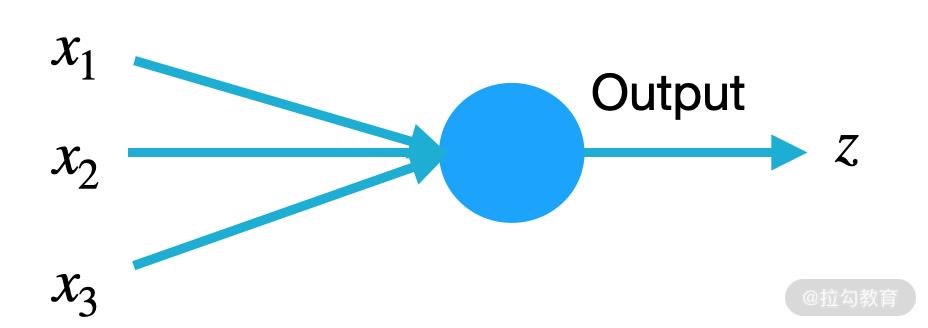
z 的计算方式如下：

其中，x1,x2,…,xk 为输入；w1,w2,…,wk 为权重；b 为偏移项；δ 则为激活函数。关于激活函数，我会在后面多个课时反复提及，这是一个相当重要的概念。

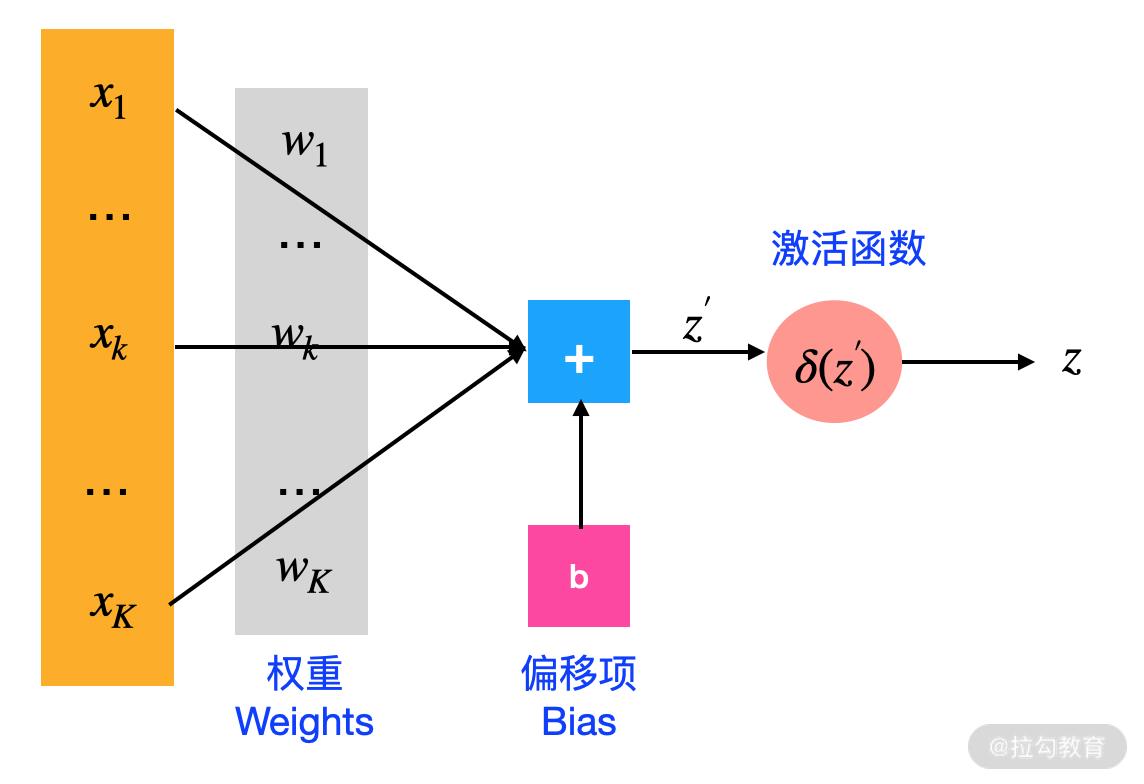
我们可以看出，一个神经元是由下面 5 部分组成的：

1. 输入：x1,x2,…,xk。
2. 权重：w1,w2,…,wk。权重的个数与神经元输入的个数相同。
3. 偏移项：可省。
4. 激活函数：一般都会有，根据实际问题也是可以省略的。
5. 输出。

w1,w2,…,wk 与 b 是神经网络需要通过训练学习到的参数。如何通过训练获得 w1, w2,…wk 与 b 是我会在《04 | 函数与优化方法：模型的自我学习（上）》与《05 | 前馈网络与反向传播：模型的自我学习（下）》中讲到。
学习一个网络、训练一个模型这样的术语，其实这些说的都是学习模型的参数，也就是我们神经元中的权重与偏移项。

Sigmoid 函数

二分类问题我们一般采用 Sigmoid 函数，多分类问题我们采用 Softmax 函数，卷积神经网络的中间层一般会采用 relu 函数。

今天我们讲的神经元最基本的作用就是用于二分类问题，也就是说上文中的 δ，它在神经元中是一个 Sigmoid 函数，作用是将神经元的输出转换为概率，为二分类问题提供概率依据。

Sigmoid 函数定义如下：

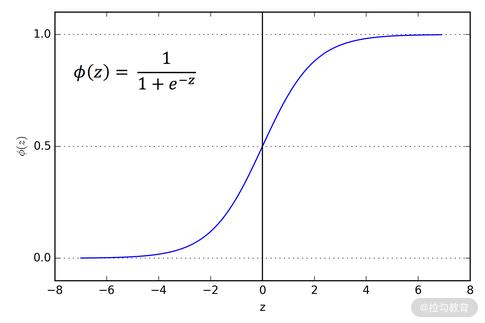
Sigmoid 函数是我们在机器学习与深度学习中经常使用的一种激活函数。通过图像我们不难发现：

1. 当输入趋近于无穷大的时候，输出越接近于 1；
2. 当输入趋近于无穷小的时候，输出越接近于 0。

所以 Sigmoid 函数经常被使用在二分类问题，它可以将 1 个数值转换为概率。

MNIST 数据集

MNIST 数据集收集了 250 名不同的人的手写数字，每张图的大小是 28x28 像素的灰度图。

我们现在需要利用神经元判断下面这张图片是否为手写数字 5：

因为每张图片是 28x28 像素的，所以我们将图片按行列展开为 x1, x2,…,x784，输入的下标的范围是 1 到 784。将它们输入到以{w1, w2, …, w784; b}为参数的神经元中。假设输出 z 为 20，经过 Sigmoid 函数我们会将 z 转换为概率，通过计算可得概率为 99%。如下图所示：

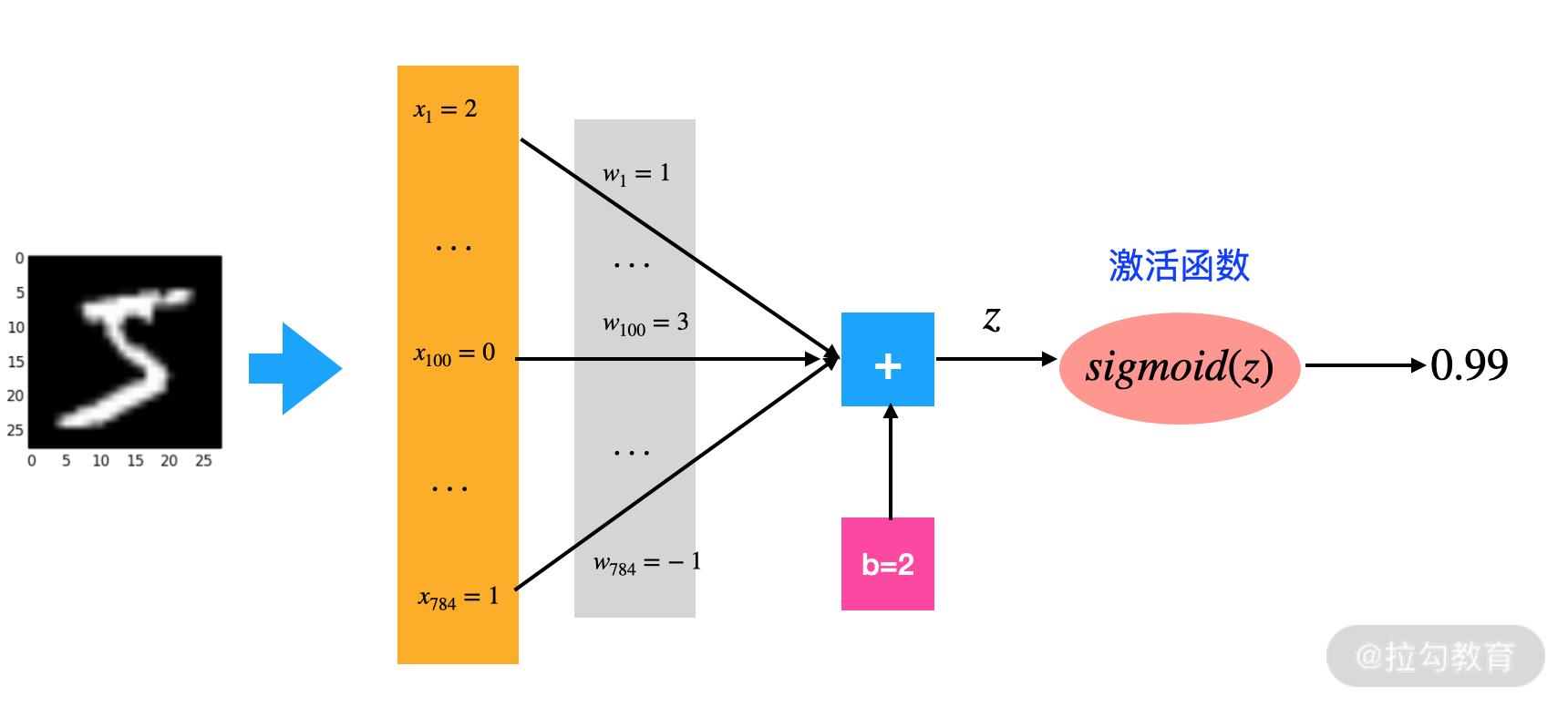
在判断的时候我们一般会以 50% 为阈值，但我们可以根据实际问题来设置不同的阈值。这里我们设定阈值为 50%，通过上图得出的 99% 明显高于这个值，因此，我们可以判断这张图片是数字 5。如此一来，就完成了一次神经元的推断过程。

其实到这里，你就已经了解了感知机的概念。没错，这一个小小的神经元就是最简单的一种感知机。神经元是模仿单个神经细胞的工作状态，单个神经细胞只有两种状态，激活时状态为是，未激活时状态为否，其实就是一个二分类问题。

如果我们需要自动识别出每张图片是属于哪一个数字，我们只要再引入一“层”。判断满足该层中满足哪个数字的概率。如下图所示。

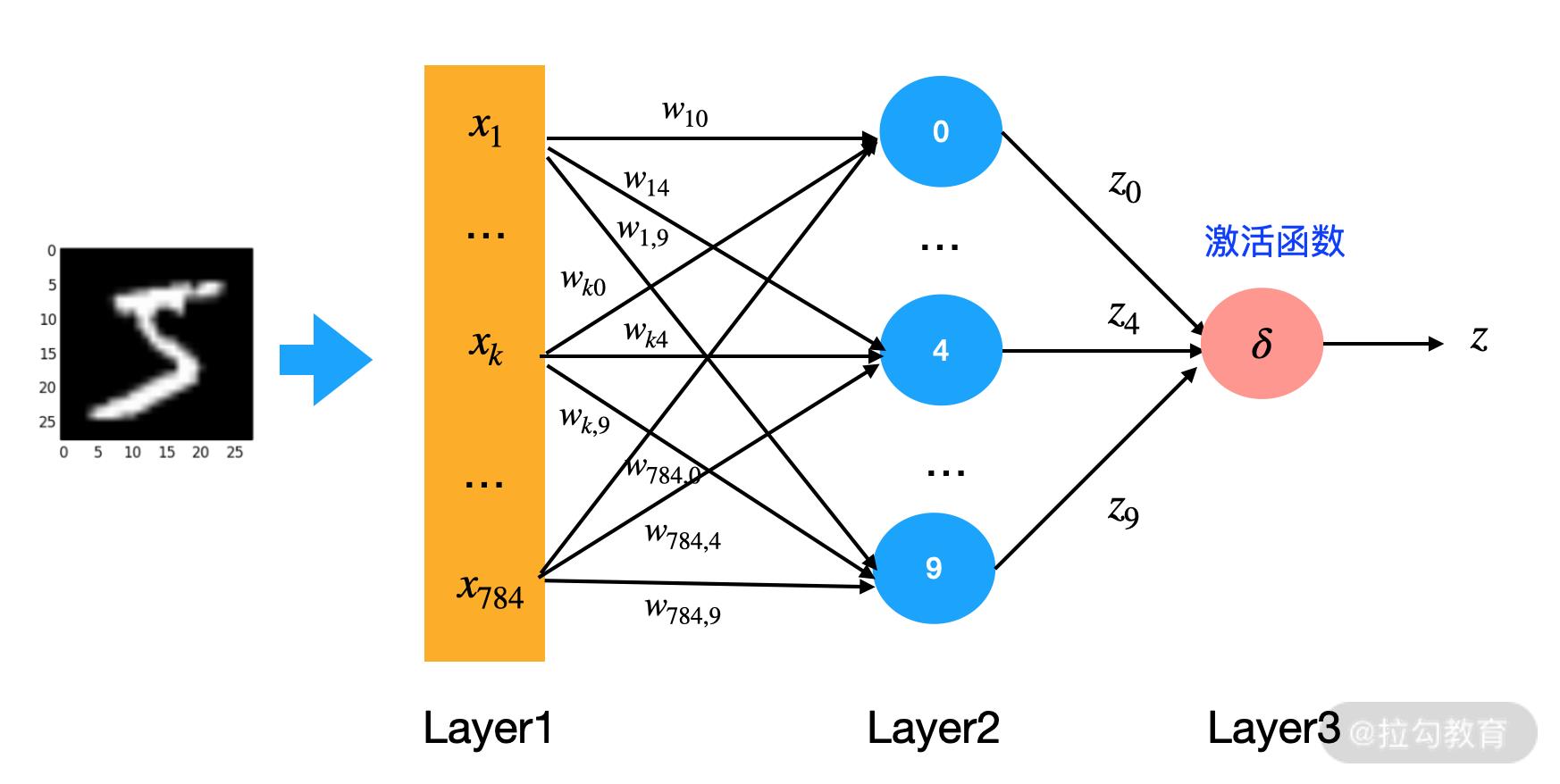
输入不变，我们仍然将一张 28x28 像素的图片转换为长度为 784 的向量。我将神经元的个数由 1 变为了 10，这 10 个神经元只负责自己力所能及的任务，它们只判断输入的图片是否为自己对应的数字，也就是神经元 0 只负责学习输入的图片是否为 0，神经元 1 只负责学习输入的图片是否为 1，以此类推。

每个神经元接受输入后都会有一个输出（图中的 z0,…,z9），每个输出 z 都是神经元自己做出的判断：输入的图片是否为该神经元负责的类别。

接下来，我们汇总一下这 10 个神经元的判断，做一个最终的推断。我们可以把图中粉色的激活函数设置为 Softmax 函数，哪个神经元输出的数值最大，输入的图片就对应哪一类。

Softmax 函数与单层感知机

神经元最终输出的 z 又可以叫作特征值。通常来说，特征值的用途不大，我们更希望获得到更有统计学意义的，每一个分类的概率。Softmax 函数可以将一组数值映射到[0，1]区间内，并且保证输出的和是 1，输出的数值可以看作“概率”。计算公式及举例如下图所示：

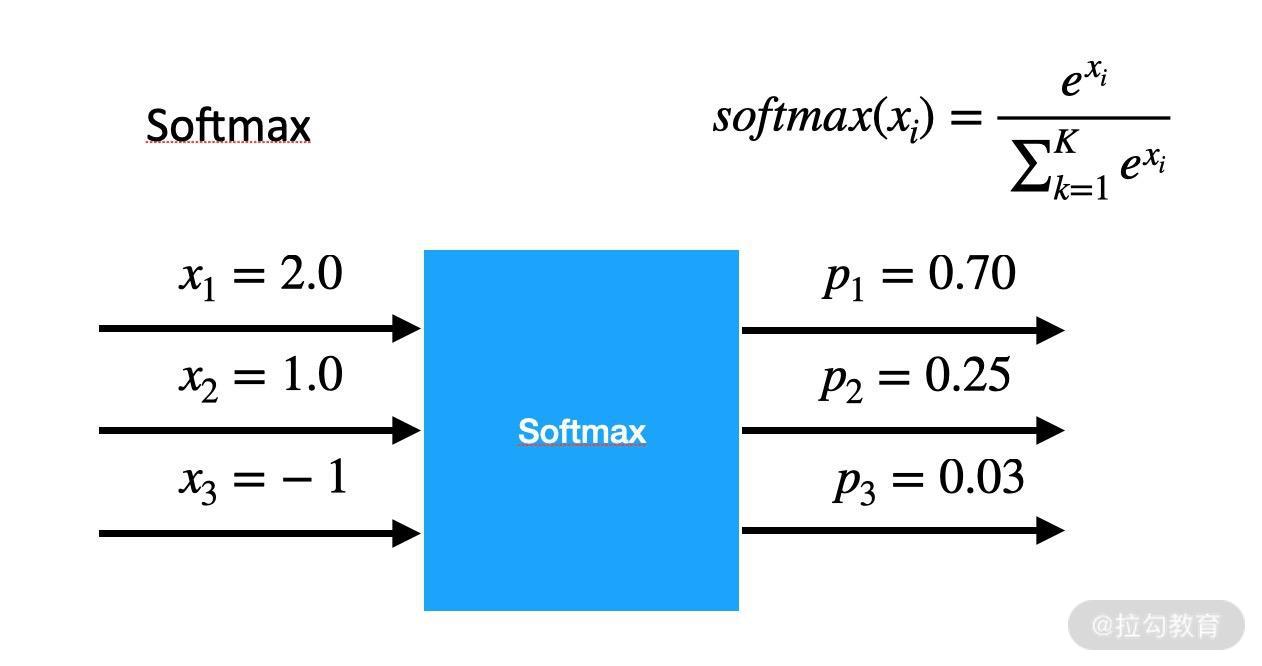
这样，我们将输出的 z0, z1, …, z9 输入到 Softmax 激活函数后，可以获得一组概率值。通过判断哪个神经元输出的概率最大，就可以推断出输入图片所属的类别。

这也引出感知机的另一种形态，单层感知机。

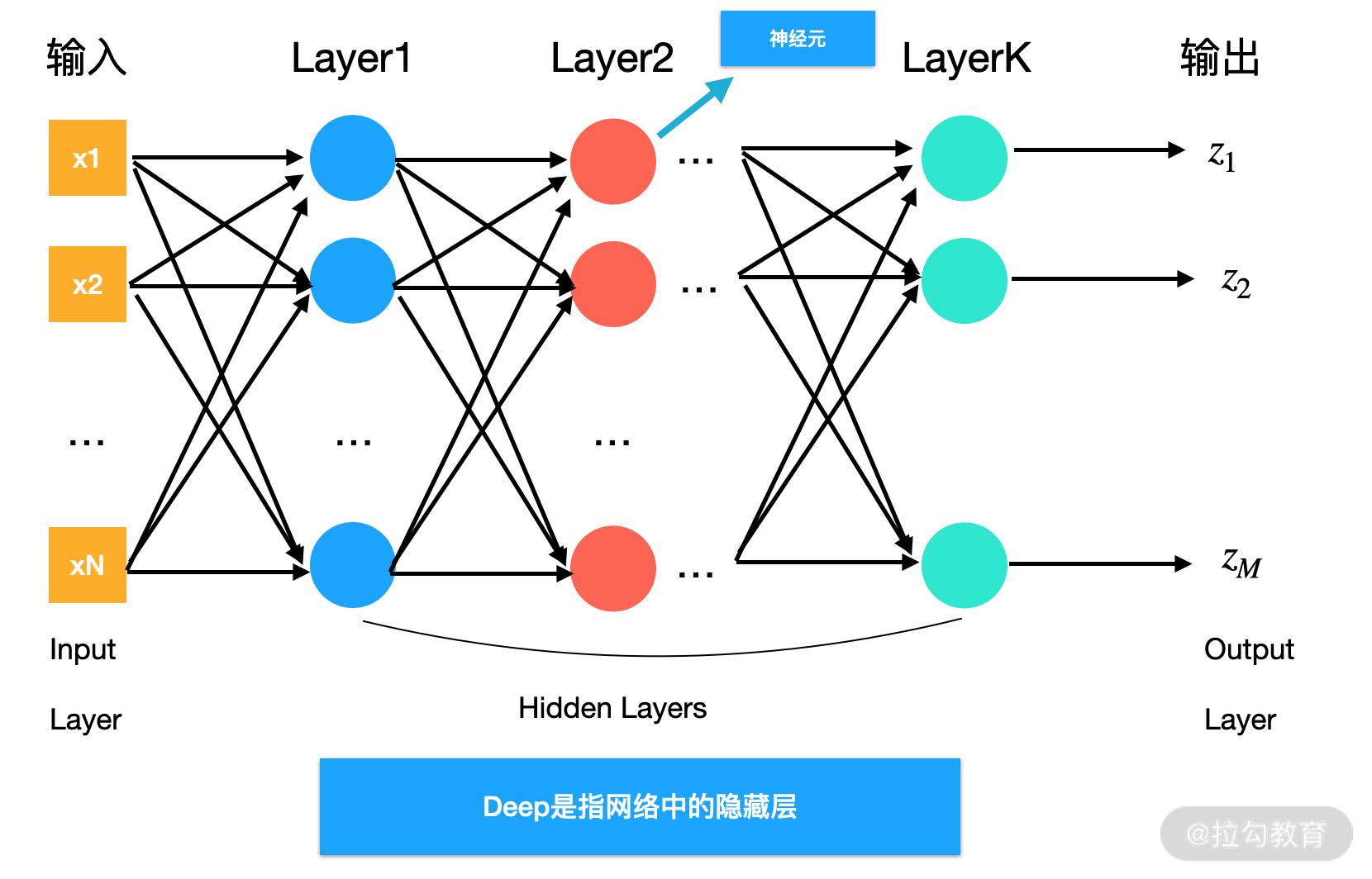
请看下图，蓝色的圆圈就是我们刚才讲的神经元，因为单个神经元的学习能力有限，所以我们对神经元进行了扩充。每个神经元各司其职，只处理自己的事情，合并起来就可以处理更复杂的问题，简单来说就是人多力量大。

在这里我会再引入“层（Layer）”的概念。

一般来说 Layer1 为输入层，Layer3 为输出层，中间的 Layer2 为隐藏层。单层感知机里只有一个隐藏层，而在后面要学习的多层感知机，以及《07 | 卷积神经网络：给你的模型一双可以看到世界的眼睛》中讲到的卷积神经网络，则会有多个隐藏层。

多层感知机

我们后续会学到卷积神经网络、时间递归神经网络等，这些都是神经网络的变种。最基本、最简单的神经网络结构就是我在这里要讲的多层感知机，只有理解了多层感知机才能更好地理解那些高级的神经网络。

我们再回到刚才识别一张图片是否为手写数字 5 的例子，这次我们有 2 个隐藏层。如下图所示：

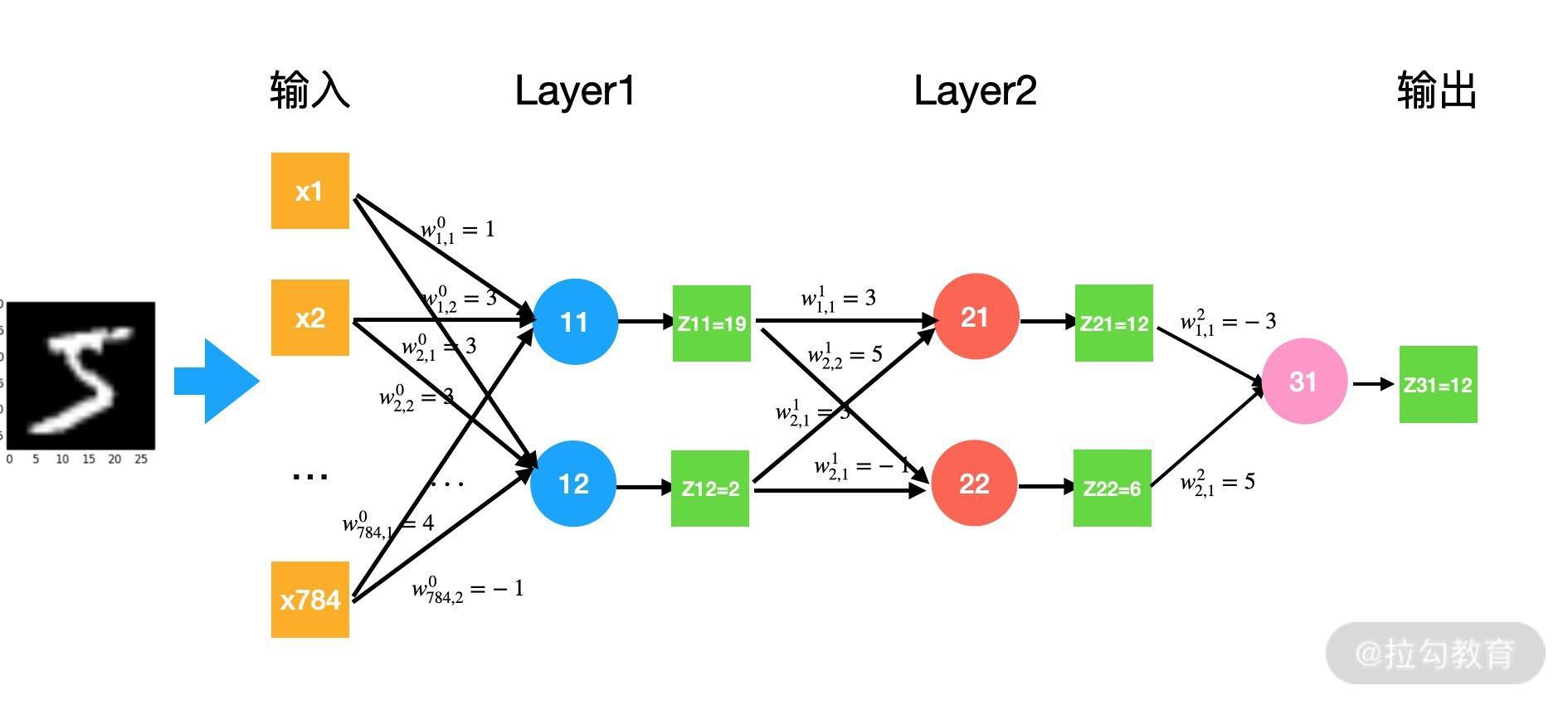
输入仍然是 x1, x2, …, x784，wkij 代表第 k 层，由输入 i 到第 j 个神经元的权重，zki 为 k 层，第 i 个神经元的输出。

我们输入的图片，经过第一层获得输出 z11 与 z12，z11 与 z12 作为第二层的输入，得到第二层的输出 z21 与 z22，第二层的输出再作为第三层的输入，最后我们获得数组 z31。

z31 之后再加一个 Sigmoid 函数，将它转换为对应的概率，这个操作就和我之前讲的一样了。

层数也不是越多越好，曾有人做过实验，当神经网络隐藏层的层数大于 2 时，网络的性能会随着层数的增加而降低。

在深度学习诞生之前，这些局限性导致多层感知机的发展一度停滞。

1. 参数量膨胀：在多层感知机中，采用的是全连接的形式，每增加一层，将会来带数量级的参数增加。这非常容易导致过拟合，并且很难训练，会陷入局部的最优。
2. 梯度消失：使用 Sigmoid 函数激活的时候，会产生梯度消失的问题，使参数无法更新。

我会在后面讲到，深度学习是通过何种方式解决上述问题的。

参考

神经网络学习示例：https://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=circle&regDataset=reg-plane&learningRate=0.03&regularizationRate=0&noise=0&networkShape=4,2&seed=0.99481&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false