atcoder AGC040 A题＞＜

Posted 2021-05-25 要坚持写博客

原题链接

题目大意：给你一串字符s，如果
si=’<’: ai<a(i+1)
si=’>’: ai>a(i+1)
求所有a相加的最小。

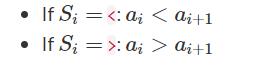
解题思路：模拟
我们先从前往后把所有的<都处理一遍，用a[i]来存储第i个位置的数的大小，即用个cnt标记，如果存在连续的就加1，不存在连续的就cnt为0。
然后我们又从后往前扫一遍，这个就把>转化成了<来处理。
如果s[i]‘>’，我们就用a[i]=a[i+1]+1来更新。但这个有一个特殊情况要考虑，就是如果s[i-1]’<'时，我们的a[i]=max(a[i-1],a[i+1])+1。

代码部分：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<iostream>
#include<cmath>
#include<queue>
#include<vector>
#define IOS ios::sync_with_stdio(false);cin.tie();cout.tie(0)

using namespace std;
typedef long long ll;
const int N=5e5+100;

map<char,int> q;
ll a[N];
string str;

int main()
{
    IOS;
    cin>>str;
    int n=str.size()+1;
    ll sum=0;
    ll cnt=0;

    for(int i=0;i<n;i++)
    {
        a[i]=max(a[i],cnt);
        if(str[i]=='<'&&i<str.size())
        {
            cnt++;
        }
        else cnt=0;
    }

    for(int i=n-1;i>=-1;i--)
    {
        if(i>=0&&str[i]=='>'&&str[i-1]=='<')
        {
            a[i]=max(a[i+1],a[i-1])+1;
            continue;
        }
        if(i>=0&&str[i]=='>')
        {
            a[i]=a[i+1]+1;
        }
    }

    for(int i=0;i<n;i++)
    {
        sum+=a[i];
    }
    cout<<sum<<endl;
    return 0;
}

鉴于有些同学说有点不是很明白，所以我又写了一种更容易懂的代码，思路类似上面的。因为我的思路是每一个符号给他改成一个数，用a[i]记忆，ai的个数比str的个数（可能表述不是很官方，字面意思）要多一个。所以我们在str后加一个‘<’符号。这样我们就可以和原式相对应了。这样我们在第一个for循环有所更改。第一次循环如果’<'是就更新，连续小于就用cnt记忆。（与上面思路类似）

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<iostream>
#include<cmath>
#include<queue>
#include<vector>
#define IOS ios::sync_with_stdio(false);cin.tie();cout.tie(0)

using namespace std;
typedef long long ll;
const int N=5e5+100;
const int maxn=110;

map<string,int> q;
ll dp[maxn][maxn];
char g[maxn][maxn];
bool col[N],row[N];
string str;
ll a[N];

int main()
{
    IOS;
    cin>>str;
    str+='<';
    int n=str.size();
    ll sum=0;
    ll cnt=0;

    for(int i=0;i<n;i++)
    {
        if(str[i]=='<'&&i<str.size())
        {
            a[i]=max(a[i],cnt);
            cnt++;
        }
        else cnt=0;
    }

    for(int i=n-1;i>=-1;i--)
    {
        if(i>=0&&str[i]=='>'&&str[i-1]=='<')
        {
            a[i]=max(a[i+1],a[i-1])+1;
            continue;
        }
        if(i>=0&&str[i]=='>')
        {
            a[i]=a[i+1]+1;
        }
    }

    for(int i=0;i<n;i++)
    {
        sum+=a[i];
    }
    cout<<sum<<endl;
    return 0;
}