优化求解基于遗传算法求解电力系统最优潮流问题matlab源码
Posted Matlab走起
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了优化求解基于遗传算法求解电力系统最优潮流问题matlab源码相关的知识，希望对你有一定的参考价值。
一、简介
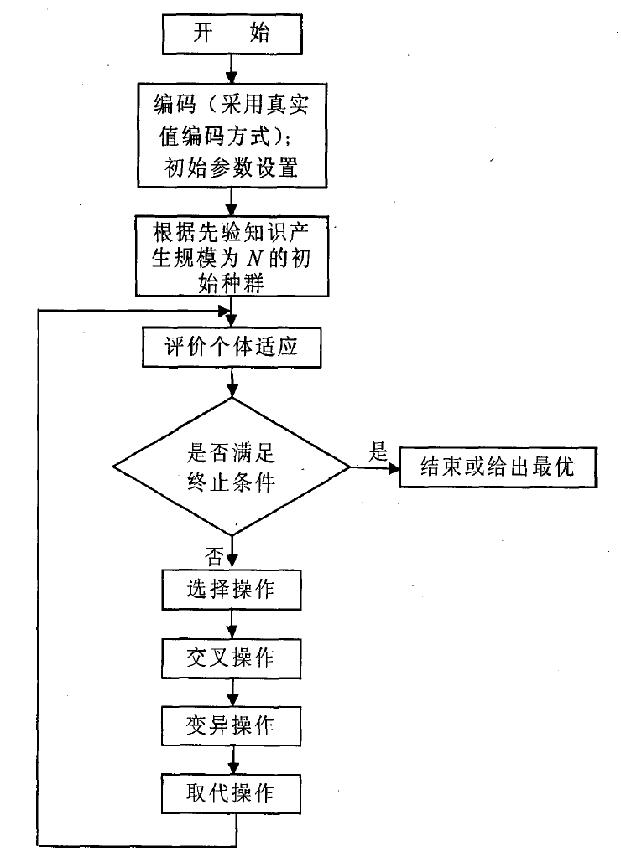
遗传算法的应用步骤
遗传算法GA是基于进化和遗传理论而提出来的全局寻优方法。
简单遗传算法解决问题的基本步骤如下：
（1）初始化：随机生成N个个体作为初始群体P(0)，该种群就是目标函数可行解的一个集合。设置进化代数计数器归零，设置最大进化代数iter_max；
（2）个体评价：将初始种群代入目标函数中，根据适应度函数计算当前群体中各个种群的适应度；
（3）终止条件判断：给出终止条件，判断算法是否满足终止条件，若满足则转到（8）；
（4）选择运算：对初始群体执行选择操作，优良的个体被大量复制，劣质的个体复制的少甚至被淘汰；
（5）交叉运算：以交叉概率来进行交叉运算；
（6）变异运算：以变异概率来进行交叉运算；
（7）群体P(t)经过选择运算、交叉运算、变异运算之后，得到由N个新个体构成的下一代群体P(t+1)，则转（2），否则转（4）；
（8）不断的进化，最终会得到目标函数中，适应度最高的个体，将其作为问题的最优解或满意解输出，终止计算。
二、源代码
function [F1 Pgg vv TL]=opf1(x)
%x表示0-1之间的随机数，结合发电功率的范围可以初始化一个发电向量
% F1表示最终的发电代价
% Pgg表示最优的发电功率
% vv表示最优发电点的电压
% TL表示耗损
% x=[0.5 0.5 0.5 0.5 0.5];
% IEEE 30-BUS TEST SYSTEM (American Electric Power)
% Bus Bus Voltage Angle ---Load---- -------Generator----- Injected
% No code Mag. Degree MW Mvar MW Mvar Qmin Qmax Mvar
busdata=[1 1 1.06 0.0 0.0 0.0 0.0 0.0 0 0 0
2 2 1.043 0.0 21.70 12.7 40.0 0.0 -40 50 0
3 0 1.0 0.0 2.4 1.2 0.0 0.0 0 0 0
4 0 1.06 0.0 7.6 1.6 0.0 0.0 0 0 0
5 2 1.01 0.0 94.2 19.0 0.0 0.0 -40 40 0
6 0 1.0 0.0 0.0 0.0 0.0 0.0 0 0 0
7 0 1.0 0.0 22.8 10.9 0.0 0.0 0 0 0
8 2 1.01 0.0 30.0 30.0 0.0 0.0 -10 60 0
9 0 1.0 0.0 0.0 0.0 0.0 0.0 0 0 0
10 0 1.0 0.0 5.8 2.0 0.0 0.0 -6 24 19
11 2 1.082 0.0 0.0 0.0 0.0 0.0 0 0 0
12 0 1.0 0 11.2 7.5 0 0 0 0 0
13 2 1.071 0 0 0.0 0 0 -6 24 0
14 0 1 0 6.2 1.6 0 0 0 0 0
15 0 1 0 8.2 2.5 0 0 0 0 0
16 0 1 0 3.5 1.8 0 0 0 0 0
17 0 1 0 9.0 5.8 0 0 0 0 0
18 0 1 0 3.2 0.9 0 0 0 0 0
19 0 1 0 9.5 3.4 0 0 0 0 0
20 0 1 0 2.2 0.7 0 0 0 0 0
21 0 1 0 17.5 11.2 0 0 0 0 0
22 0 1 0 0 0.0 0 0 0 0 0
23 0 1 0 3.2 1.6 0 0 0 0 0
24 0 1 0 8.7 6.7 0 0 0 0 4.3
25 0 1 0 0 0.0 0 0 0 0 0
26 0 1 0 3.5 2.3 0 0 0 0 0
27 0 1 0 0 0.0 0 0 0 0 0
28 0 1 0 0 0.0 0 0 0 0 0
29 0 1 0 2.4 0.9 0 0 0 0 0
30 0 1 0 10.6 1.9 0 0 0 0 0];
% Line code
% Bus bus R X 1/2 B = 1 for lines
% nl nr p.u. p.u. p.u. > 1 or < 1 tr. tap at bus nl
linedata=[1 2 0.0192 0.0575 0.02640 1
1 3 0.0452 0.1852 0.02040 1
2 4 0.0570 0.1737 0.01840 1
3 4 0.0132 0.0379 0.00420 1
2 5 0.0472 0.1983 0.02090 1
2 6 0.0581 0.1763 0.01870 1
4 6 0.0119 0.0414 0.00450 1
5 7 0.0460 0.1160 0.01020 1
6 7 0.0267 0.0820 0.00850 1
6 8 0.0120 0.0420 0.00450 1
6 9 0.0 0.2080 0.0 0.978
6 10 0 .5560 0 0.969
9 11 0 .2080 0 1
9 10 0 .1100 0 1
4 12 0 .2560 0 0.932
12 13 0 .1400 0 1
12 14 .1231 .2559 0 1
12 15 .0662 .1304 0 1
12 16 .0945 .1987 0 1
14 15 .2210 .1997 0 1
16 17 .0824 .1923 0 1
15 18 .1073 .2185 0 1
18 19 .0639 .1292 0 1
19 20 .0340 .0680 0 1
10 20 .0936 .2090 0 1
10 17 .0324 .0845 0 1
10 21 .0348 .0749 0 1
10 22 .0727 .1499 0 1
21 22 .0116 .0236 0 1
15 23 .1000 .2020 0 1
22 24 .1150 .1790 0 1
23 24 .1320 .2700 0 1
24 25 .1885 .3292 0 1
25 26 .2544 .3800 0 1
25 27 .1093 .2087 0 1
28 27 0 .3960 0 0.968
27 29 .2198 .4153 0 1
27 30 .3202 .6027 0 1
29 30 .2399 .4533 0 1
8 28 .0636 .2000 0.0214 1
6 28 .0169 .0599 0.065 1];
gencost = [1 0.00375 2 0 50 200;
2 0.0175 1.75 0 20 80;
5 0.0625 1 0 15 50;
8 0.0083 3.25 0 10 35;
11 0.025 3 0 10 30;
13 0.025 3 0 12 40];
% formation of Y bus
j=sqrt(-1);
nl = linedata(:,1); nr = linedata(:,2); R = linedata(:,3);
X = linedata(:,4); Bc = j*linedata(:,5); a = linedata(:, 6);
nbr=length(linedata(:,1)); nbus = max(max(nl), max(nr));
Z = R + j*X; y= ones(nbr,1)./Z; %branch admittance
for n = 1:nbr
if a(n) <= 0 a(n) = 1;
else end
Ybus=zeros(nbus,nbus); % initialize Ybus to zero
% formation of the off diagonal elements
for k=1:nbr;
Ybus(nl(k),nr(k))=Ybus(nl(k),nr(k))-y(k)/a(k);
Ybus(nr(k),nl(k))=Ybus(nl(k),nr(k));
end
end
% formation of the diagonal elements
for n=1:nbus
for k=1:nbr
if nl(k)==n
Ybus(n,n) = Ybus(n,n)+y(k)/(a(k)^2) + Bc(k);
elseif nr(k)==n
Ybus(n,n) = Ybus(n,n)+y(k) +Bc(k);
else,
end
end
end
%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%
nn1=length(gencost(:,1));
for ii=1:nn1
if x(ii)>1
x(ii)=1;
elseif x(ii)<0
x(ii)=0;
end
y1(ii)=gencost(ii,5)+x(ii)*(gencost(ii,6)-gencost(ii,5));
% busdata=[1 1 1.06 0.0 0.0 0.0 0.0 0.0 0 0 0
% 2 2 1.043 0.0 21.70 12.7 40.0 0.0 -40 50 0
% 3 0 1.0 0.0 2.4 1.2 0.0 0.0 0 0 0
% 4 0 1.06 0.0 7.6 1.6 0.0 0.0 0 0 0
% 5 2 1.01 0.0 94.2 19.0 0.0 0.0 -40 40 0
% 6 0 1.0 0.0 0.0 0.0 0.0 0.0 0 0 0
% 7 0 1.0 0.0 22.8 10.9 0.0 0.0 0 0 0
% 8 2 1.01 0.0 30.0 30.0 0.0 0.0 -10 60 0
% 9 0 1.0 0.0 0.0 0.0 0.0 0.0 0 0 0
% 10 0 1.0 0.0 5.8 2.0 0.0 0.0 -6 24 19
% 11 2 1.082 0.0 0.0 0.0 0.0 0.0 0 0 0
% 12 0 1.0 0 11.2 7.5 0 0 0 0 0
% 13 2 1.071 0 0 0.0 0 0 -6 24 0
% 14 0 1 0 6.2 1.6 0 0 0 0 0
% 15 0 1 0 8.2 2.5 0 0 0 0 0
% 16 0 1 0 3.5 1.8 0 0 0 0 0
% 17 0 1 0 9.0 5.8 0 0 0 0 0
% 18 0 1 0 3.2 0.9 0 0 0 0 0
% 19 0 1 0 9.5 3.4 0 0 0 0 0
% 20 0 1 0 2.2 0.7 0 0 0 0 0
% 21 0 1 0 17.5 11.2 0 0 0 0 0
% 22 0 1 0 0 0.0 0 0 0 0 0
% 23 0 1 0 3.2 1.6 0 0 0 0 0
% 24 0 1 0 8.7 6.7 0 0 0 0 4.3
% 25 0 1 0 0 0.0 0 0 0 0 0
% 26 0 1 0 3.5 2.3 0 0 0 0 0
% 27 0 1 0 0 0.0 0 0 0 0 0
% 28 0 1 0 0 0.0 0 0 0 0 0
% 29 0 1 0 2.4 0.9 0 0 0 0 0
% 30 0 1 0 10.6 1.9 0 0 0 0 0];
%
% % Line code
% % Bus bus R X 1/2 B = 1 for lines
% % nl nr p.u. p.u. p.u. > 1 or < 1 tr. tap at bus nl
% linedata=[1 2 0.0192 0.0575 0.02640 1
% 1 3 0.0452 0.1852 0.02040 1
% 2 4 0.0570 0.1737 0.01840 1
% 3 4 0.0132 0.0379 0.00420 1
% 2 5 0.0472 0.1983 0.02090 1
% 2 6 0.0581 0.1763 0.01870 1
% 4 6 0.0119 0.0414 0.00450 1
% 5 7 0.0460 0.1160 0.01020 1
% 6 7 0.0267 0.0820 0.00850 1
% 6 8 0.0120 0.0420 0.00450 1
% 6 9 0.0 0.2080 0.0 0.978
% 6 10 0 .5560 0 0.969
% 9 11 0 .2080 0 1
% 9 10 0 .1100 0 1
% 4 12 0 .2560 0 0.932
% 12 13 0 .1400 0 1
% 12 14 .1231 .2559 0 1
% 12 15 .0662 .1304 0 1
% 12 16 .0945 .1987 0 1
% 14 15 .2210 .1997 0 1
% 16 17 .0824 .1923 0 1
% 15 18 .1073 .2185 0 1
% 18 19 .0639 .1292 0 1
% 19 20 .0340 .0680 0 1
% 10 20 .0936 .2090 0 1
% 10 17 .0324 .0845 0 1
% 10 21 .0348 .0749 0 1
% 10 22 .0727 .1499 0 1
% 21 22 .0116 .0236 0 1
% 15 23 .1000 .2020 0 1
% 22 24 .1150 .1790 0 1
% 23 24 .1320 .2700 0 1
% 24 25 .1885 .3292 0 1
% 25 26 .2544 .3800 0 1
% 25 27 .1093 .2087 0 1
% 28 27 0 .3960 0 0.968
% 27 29 .2198 .4153 0 1
% 27 30 .3202 .6027 0 1
% 29 30 .2399 .4533 0 1
% 8 28 .0636 .2000 0.0214 1
% 6 28 .0169 .0599 0.065 1];
% gencost = [1 0.00375 2 0 50 200;
% 2 0.0175 1.75 0 20 80;
% 5 0.0625 1 0 15 50;
% 8 0.0083 3.25 0 10 35;
% 11 0.025 3 0 10 30;
% 13 0.025 3 0 12 40];
end
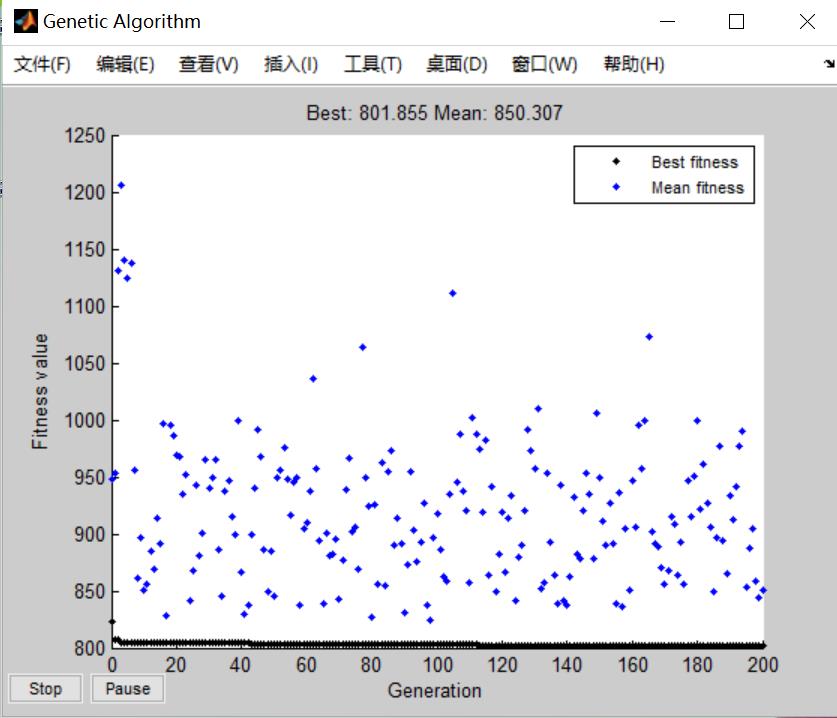
三、运行结果
四、备注
完整代码或者仿真咨询添加QQ1575304183
以上是关于优化求解基于遗传算法求解电力系统最优潮流问题matlab源码的主要内容，如果未能解决你的问题，请参考以下文章
优化求解基于matlab遗传算法求解电动汽车充电管理优化问题含Matlab源码 1178期
车间调度基于遗传算法求解混合流水车间调度最优问题matlab源码
车间调度基于遗传算法求解混合流水车间调度最优问题matlab源码