cache的基本原理

Posted 2021-05-24 jtwty

目录

• • 一.cache结构（直接映射）
  • • （1）定义
    • （2）分析
  • 二.cache访问
  • • （1）求cache的总位数
    • （2）举例
  • 三.cache缺失处理（cache miss)
  • 四.写操作处理

---

cache是指 高速缓冲存储器 ，它最接近CPU。cache中保存了最近所访问过的数据项的集合，如果当前CPU所访问的数据项不在cache，那么就会造成一次缺失，然后将该数据调入cache中。

cache的操作可以分为读操作和写操作，读操作不会改变值，较为简单。

---

一.cache结构（直接映射）

（1）定义

总的来说，cache是主存与CPU之间的桥梁，cache需要根据主存地址为主存中的每一个字分配一个位置。这种结构叫做直接映射。

映射方法

（块地址）mod （cahce中的块数）

（2）分析

话不多说，直接上图。

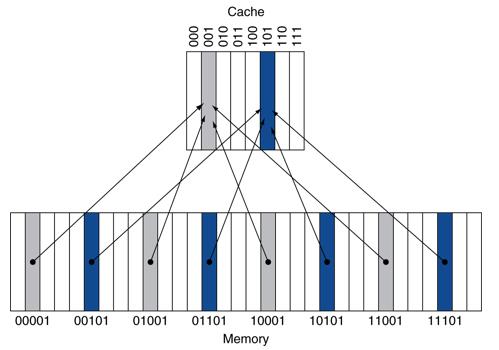
该模型具体讲解：

在上图所示的结构中，cache一共为8块，那么cache的地址划分只需要取三位地址就可以全部表示，即从000-111。

下面的主存一共被划分为32块，因为 32/8=4，所以需要划分四个片区，每个片区里面均为8块。当我们要区分四个片区时，需要拿两位地址来表示，即从00-11。然后每个片区里面的地址都从000-111，在这之前加上片区的地址就构成了完整的地址。

但是问题又来了，按上图cache中一个块就对应主存中的四个位置，我们怎么知道现在cache中的数据项是不是所请求的字呢？

第一步（添加标记tag）：就是上面所解释的，对于主存中每一个块都由5位地址组成，而地址的高两位进行分片作为标记位（标记只需要高两位），地址第三位的索引域用来选择具体的位置。

第二步（添加有效位V）：当CPU发生请求时，有可能cache中此时并没有数据，那么标记域就没有用，因此我们加一个有效位来表示当前该位置有没有被设置。

二.cache访问

cache具有时间局限性，最近访问过的字会替换掉较早访问的字。（当两个字索引域相同，只要标记域不同时。）

（1）求cache的总位数

要求：

使用32位的地址，直接映射cache。

cache中有2ⁿ个块，此时使用n为来进行索引（索引域）

块大小为2^m个字（2^m+2个字节），因此m位用来查找块中的字，两位是字节偏移信息。

标记域的大小为：32-（n+m+2）

直接映射的cache的总位数为：2ⁿ ×（块大小+标记域大小+有效位域大小）即为：2ⁿ ×（2^m × 2⁵ + (32-n-m-2) + 1)

（2）举例

假设有一个直接映射cache，有16KiB的数据，块大小为4个字，地址为32位，那么该cache一共需要多少位？

解：
因为16KiB是4096（2¹²）个字，块大小为2²，那么就有2¹⁰个块。每个块大小为：2² * 2⁵ = 2⁷ 个数据位，又有32-10-2-2=18位的标记域，再加一个有效位，那么总cache为：2¹⁰×（2⁷ + 18 +1)=2¹⁰×147=147Kib

三.cache缺失处理（cache miss)

概念： 由于数据不再cache中而导致被请求的数据不能满足。分为指令缺失以及数据缺失。

指令cache缺失处理：

（1）把程序计数器（PC）的原始值（当前PC-4）送入存储器中。（因为要执行下一条指令，PC已经+4了，所以我们要减回去。）

（2）通知主存进行一次读操作，并等待主存访问完成。

（3)写cache项，将主存得到的数据写回cache中，并将地址高位写入标记域，设置有效位。

（4）重启指令执行第一步，这次指令就在cache中。

数据cache缺失处理：

与上述基本相同，直到从存储器中取回数据后才发生响应。

四.写操作处理

当我们遇到store指令时，将该数据写入cache中，当时此时cache与主存相应位置的值就不一样，我们需要对此进行处理。

方法一：写直达（写穿/写通过）write—through

就是我们在更改数据项时，同时更新cache和下一存储器，保持二值的一致性。

优化：如果我们遇到一个store指令就完整的写穿一次，那么运行的效率将会大大的降低。此时我们可以采取写缓冲（write buffer），将数据同时写入cache和缓冲中，然后继续执行写一个任务，当缓冲满后或者写操作完成后，再将缓冲里面的值写入主存中。

方法二：写回 write—back

当发生写操作时，我们只把cache里面的值更新，只有当该位置再次被替换时，我们才将该值写入较低的存储结构中。这样写操作就变得非常快。

缺点：写回机制的实现比写直达复杂的多。