图的应用——最短路径（迪杰斯特拉算法）

Posted 2021-05-24 Rainbowman 0

Content

• 1. 什么是最短路径
• 2. 迪杰斯特拉算法【O(n^2^)】
• 3. 代码
• 4. 迪杰斯特拉算法 VS 普利姆算法

1. 什么是最短路径

在一个带权有向图中，从某一顶点到另一顶点可能有很多条路径，最短路径即权值之和最小的那条路径。

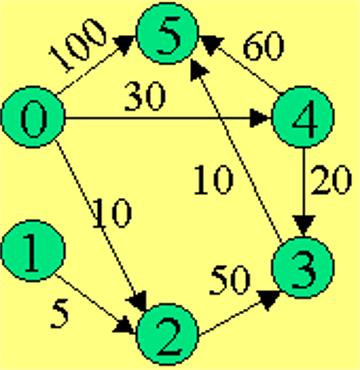
如在上图中，从顶点0到顶点5的最短路径是0-4-3-5，长度为60。

2. 迪杰斯特拉算法【O(n²)】

该算法用到了贪心的思想，设 v0为源点，S 为已求得的最短路径的终点集合； 则下一条最短路径。( 设其终点为 v)或者是弧 < v0, v>, 或者是中间只经过 S 中的顶点而最后到达顶点 v0 的路径。

（下面的步骤和代码都是为了实现这一思想）

首先定义一些符号的含义

符号	形式	含义
v0	int	源点的下标
S	集合	目前为止找到最短路径的顶点集合
T	集合	目前为止还没有找到最短路径的顶点集合
D[i]	int一维数组	表示目前为止从源点v0经过S集合中的顶点到T集合中的顶点i的最短路径长度
Final[i]	bool一维数组	Final[i]=true表示顶点i在集合S中， Final[i]=false表示顶点i在集合T中
P[i][j]	bool二维数组	P[i]一整行中有一个为true（Eg：P[i][j]=true），则表示从源点v0到顶点i存在最短路径，且目前为止顶点j在最短路径上。若P[i]一整行都为false，则表示从源点v0到顶点i目前不存在路径

步骤：

（1）将图中的顶点分为S和T两个集合，初始时，S集合中只包含源点v0，T集合中包含除源点v0外的所有顶点。

D[i]表示目前为止，从源点v0经过S集合中的顶点到T集合中顶点的最小值。

初始时，D[i]数组中存的是与顶点v0直接连接的顶点的路径长度。

（2）遍历数组D，找到最小值D[v]，将顶点v加入到集合S中（Final[v]=true）

（3）由于顶点v从T集合中加入到S集合，所以需要更新数组D[i]（参考上述D[i]的含义）

（4）重复（2）、（3），直到S集合中包含所有的顶点（如果图中有n个顶点，则需要遍历n-1次），此时，对于数组D，D[i]表示从v0出发，到达i顶点所需的最短路径。

注意：

（1）数组D[i]是一直在更新的，因为随着新顶点从T集合中加入S集合，从源点v0经过S集合到达T集合中顶点i的最小值也可能发生变化。
（2）Final[i]数组的用处其实很简单，就是标志顶点i是在集合S中（Finial[i]=true）还是在T集合（Finial[i]=false）中，别把Final数组和D数组的作用搞混

说明：

如果想输出从源点v0到终点v经过哪些顶点怎么办？
此时需要用到二维数组bool P[i][j]（含义见上述表格）
对于P[i][j]，表示的从顶点v0到顶点i是否存在路径，若不存在，则P[i]一整行都为false，若存在，则对于路径上的顶点j，有P[i][j]=true
在第（3）步中，在更新数组D是，如果对于T集合中的顶点w，有D[v]+<v,w><D[w]，则说明因为v顶点加入集合S，使得从v0到w的最短路径发生变化，此时让P[w]这一行等于P[v]这一行即可。

3. 代码

代码中的注释说明的比较清楚，静下心来看看

#include <iostream>
#define MAX_VEX_NUM 20
#define INFINITY 99999
using namespace std;
typedef char NumType;
struct MGraph
{
    NumType Vex[MAX_VEX_NUM];
    int Arc[MAX_VEX_NUM][MAX_VEX_NUM];
    int VexNum;
    int EdgeNum;
};
int Locate(MGraph G,NumType v)
{
    int i;
    for(i=0;i<G.VexNum;i++)
        if(v==G.Vex[i])return i;
    return -1;
}
void CreatMGraph(MGraph &G)
{
    cout<<"请输入顶点个数："<<endl;
    cin>>G.VexNum;
    cout<<"请输入边的条数："<<endl;
    cin>>G.EdgeNum;
    int i,j,k;
    cout<<"请输入顶点信息："<<endl;
    for(i=0;i<G.VexNum;i++)cin>>G.Vex[i];
    //弧初始化
    for(i=0;i<MAX_VEX_NUM;i++)
        for(j=0;j<MAX_VEX_NUM;j++)
            G.Arc[i][j]=INFINITY;
    cout<<"请输入边的信息："<<endl;
    int w;
    NumType v1,v2;
    for(k=0;k<G.EdgeNum;k++)
    {
        cin>>v1;cin>>v2;cin>>w;
        i=Locate(G,v1);j=Locate(G,v2);
        G.Arc[i][j]=w;
    }
}

void ShortestPath_DIJ(MGraph G,NumType data)
{
    // 是否找到v0到v的最短路径
    // Final[i] = true 表示目前为止，已找到从源点v0到点i的最短路径（就是把点i加入S集合中）
    bool Final[G.VexNum];
    // 若P[i]这一整行都为false，表示从源点v0到点i不存在路径
    // 若P[i]一整行中存在一个true，如P[i][j]=true，表示源点v0到点i存在最短路径，且边i->j为最短路径上的一条边
    bool P[G.VexNum][G.VexNum];
    //D[i]表示目前为止，从源点v0到点i的最短路径长为D[i]（即源点v0经过S集合中的顶点到T集合中顶点i的最小值）
    // 注意，是截止目前，以后随着新的顶点加入S集合中，
    // D[i]的值还有可能更新（因为新顶点加入S集合，可能使得从源点v0经过S中的顶点到T中顶点i的最短路径发生变化）
    int D[G.VexNum];
    int v,w;
    int v0=Locate(G,data);
    for(v=0;v<G.VexNum;v++)
    {
        //初始化，先找到和顶点v0直接连接的顶点
        // 并用D[v]记录目前为止从源点v0到顶点v的最小值，若目前不可达则为INFINITY
        D[v]=G.Arc[v0][v];
        // 初始化
        Final[v]=false;
        for(w=0;w<G.VexNum;w++)
            P[v][w]=false;
        // 如果可以从源点v0到顶点v，则改变相应P[v][v0]为true
        if(D[v]<INFINITY)
        {
            P[v][v0]=true;
            P[v][v]=true;
        }
    }
    Final[v0]=true;D[v0]=0;
    int i,j;
    // 源点v0一开始在S集合中，T集合中有n-1个顶点
    // 每次遍历都会从T集合中挑选出一个顶点到S集合中，因此需要遍历n-1次
    // 这是算法的主体部分，有两个for循环嵌套，因此迪杰斯特拉算法的时间复杂度是O(n^2)
    for(i=1;i<G.VexNum;i++)
    {
        int minn=INFINITY;
        // Final[w]=false意味着w顶点在集合T中
        // 目的是找到目前为止，从源点v0经过S中的顶点到T中顶点w的最小值，然后将其加入S集合中
        for(w=0;w<G.VexNum;w++)
            if(minn>D[w]&&!Final[w]){minn=D[w];v=w;}
        Final[v]=true;
        // 随着新顶点v从T集合加入S集合，D[i]的值有可能需要更新
        for(w=0;w<G.VexNum;w++)
        {
            if(D[v]+G.Arc[v][w]<D[w]&&!Final[w])
            {
                // 更新
                D[w]=D[v]+G.Arc[v][w];
                // 因为顶点v加入S集合，导致产生了更短的从V0到顶点w的路径
                // 因此，到目前为止，从源点v0到顶点w的最短路径一定包含从源点v0到顶点w
                // （随着后续新顶点的加入，可能会产生更短的从源点v0到顶点w的路径，到时候再对P[w]这一行做一次更新）
                for(j=0;j<G.VexNum;j++)P[w][j]=P[v][j];
                P[w][w]=true;
            }
        }
    }
    // 输出从源点v0到剩下顶点的最短路径
    for(i=0;i<G.VexNum;i++)
    {
        bool Flag=false;
        if(i!=v0)
        {
            cout<<endl;cout<<"从"<<G.Vex[v0]<<"到"<<G.Vex[i]<<"顶点的最小路径："<<endl;
            for(j=0;j<G.VexNum;j++)
                if(P[i][j]){cout<<G.Vex[j]<<" ";Flag=true;}
            if(!Flag)cout<<"不存在路径！";
        }
    }
}
int main()
{
    MGraph G;
    CreatMGraph(G);
    ShortestPath_DIJ(G,'0');
    return 0;
}

注意：

（1）数组D[i]是一直在更新的，因为随着新顶点从T集合中加入S集合，从源点v0经过S集合到达T集合中顶点i的最小值也可能发生变化。
（2）Final[i]数组的用处其实很简单，就是标志顶点i是在集合S中（Finial[i]=true）还是在T集合（Finial[i]=false）中，别把Final数组和D数组的作用搞混

4. 迪杰斯特拉算法 VS 普利姆算法

这一点是补充，我觉得这两个算法有些地方有相似之处，但又有很大的不同，所以放在一起做一个比较。

迪杰斯特拉算法是用来求最短路径的，而普利姆算法是用来求最小生成树的。（普利姆算法求最小生成树）

普利姆算法的思想：

（1）集合V包含所有顶点，把集合V分为U和V-U两个集合。U集合表示目前找到的最小生成树中包含的顶点，V-U表示目前不包含在最小生成树中的顶点，初始时U集合中随意包含一个顶点；

集合TE为最小生成树的边的集合，一开始为空集。

（2）从U集合中的顶点<u0,u1,…,un>和V-U集合中的顶点<v0,v1,…,vm>中找到一条最短的路径<ui,vj>，将vj加入集合U，边<ui,vj>加入集合TE；

（3）重复步骤（2），直至U中包含所有顶点；则此时集合TE中的元素构成了最小生成树的所有边。

迪杰斯特拉算法的思想：

（目的是找到从源点v0到所有顶点的最短路径）

（1）有S和T两个集合，S集合中包含目前为止已找到最短路径的终点顶点，T集合中包含目前为止未找到最短路径的终点顶点；数组D[i]代表目前为止从顶点v0经过S集合中的顶点到集合T中顶点i的最小值。

（2）每次找到从源点v0出发，经过S集合中的顶点，到T集合中顶点的路径的最小值，设该值为D[v]（v是集合T中的顶点）（即路径的源点是v0，终点是T集合中的顶点v，经过集合S中的顶点）（也可以是<v0,v>）

（3）将v顶点加入S集合中，并更新数组D

（4）重复（2）、（3），直至S中包含所有顶点。此时数组D中的元素D[i]即为从源点v0到终点i的最短路径。

比较：

相似之处：

两者相似之处为都有两个顶点集合（对于普利姆算法，是集合U和V-U；对于迪杰斯特拉算法，是集合S和集合T），都是从一个集合中挑顶点到另一个集合中，直至另一个集合中包含全部顶点。

不同之处：

挑顶点的原则不同：

对于普利姆算法，每次挑的是从集合U中所有顶点到集合V-U中所有顶点中边的最小值<ui,vj>（边的开始顶点可以是集合U中的任意元素）；并把vj加入到集合U中。

对于迪杰斯特拉算法，每次挑的是以v0为源点，经过集合S中顶点，到达T集合中顶点v的最小值<v0,v>（边的开始顶点只能是v0，结束顶点可以是T集合中的任意元素）；并把v加入到集合S当中。

END：

静下心来，好好理解下。：）

参考