[DP 区间 剖分 高精] 凸多边形划分
Posted 鱼竿钓鱼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[DP 区间 剖分 高精] 凸多边形划分相关的知识,希望对你有一定的参考价值。
[DP 区间 剖分] 凸多边形划分
题目
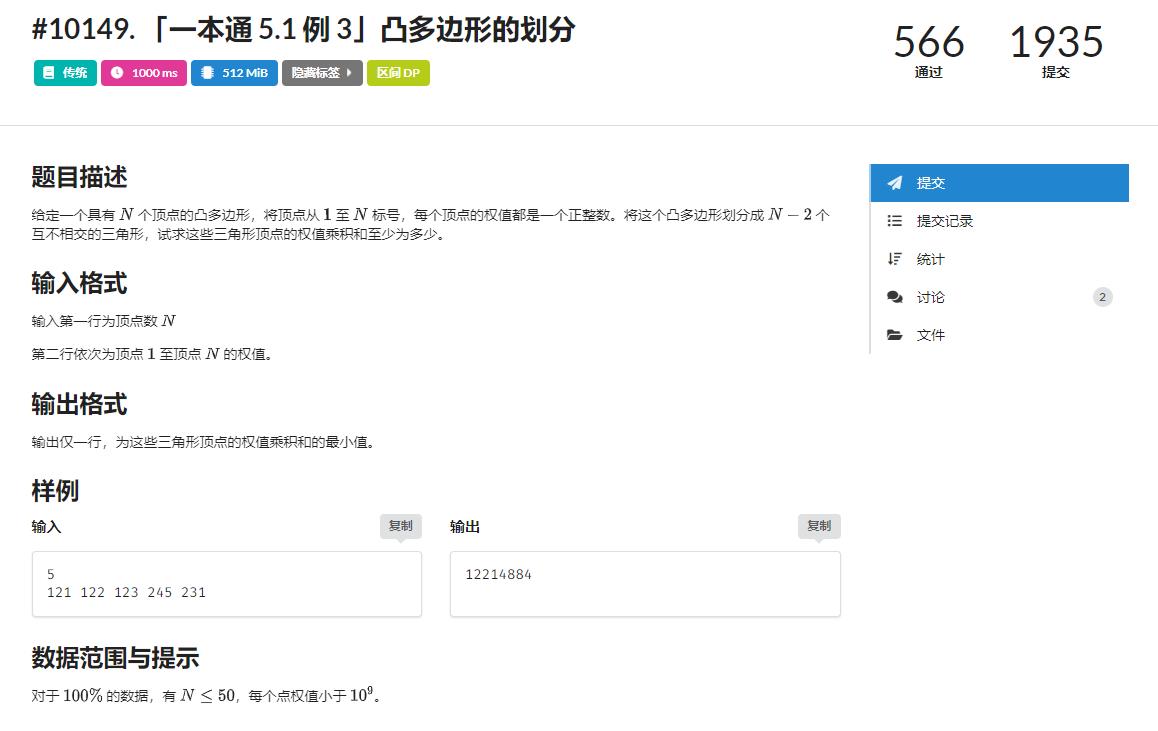
思路
剖分问题也可以转化为区间DP
因为分隔线不相交,所以剖分后可以变成多个互不影响的子问题。
定义
f
[
l
]
[
r
]
为
点
l
r
凸
多
边
形
的
最
优
划
分
f[l][r]为点l~r凸多边形的最优划分
f[l][r]为点l r凸多边形的最优划分
f
[
l
]
[
r
]
=
m
a
x
(
f
[
l
]
[
r
]
,
f
[
l
]
[
k
]
+
f
[
k
]
[
r
]
+
w
[
l
]
∗
w
[
r
]
∗
w
[
k
]
)
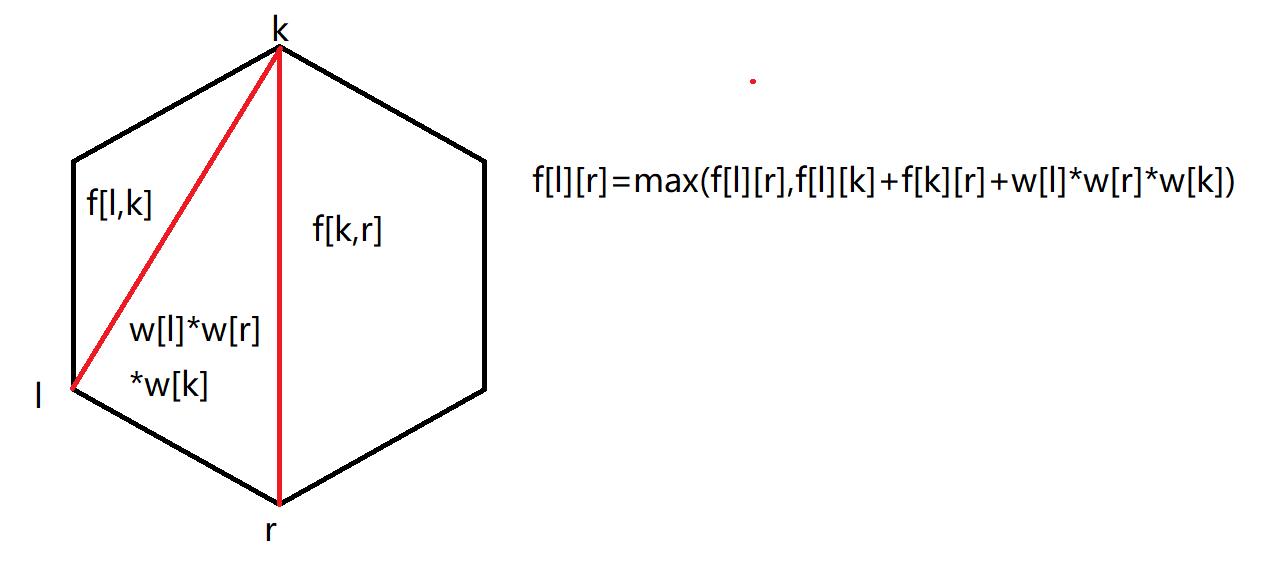
f[l][r]=max(f[l][r],f[l][k]+f[k][r]+w[l]*w[r]*w[k])
f[l][r]=max(f[l][r],f[l][k]+f[k][r]+w[l]∗w[r]∗w[k])
注意是f[k][r]而不是f[k+1][r]
目标:
f
[
1
]
[
n
]
f[1][n]
f[1][n]
代码
__int128实现高精度
#include<bits/stdc++.h>
using namespace std;
inline __int128 read(){
__int128 x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9'){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(__int128 x){
if(x < 0){
putchar('-');
x = -x;
}
if(x > 9)
print(x / 10);
putchar(x % 10 + '0');
}
const int N=55,M=35;
int n;
const __int128 INF=1e30;
__int128 w[N];
__int128 f[N][N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)w[i]=read();
for(int len=3;len<=n;len++)
for(int l=1;l+len-1<=n;l++)
{
int r=l+len-1;
f[l][r]=INF;
for(int k=l+1;k<r;k++)
f[l][r]=min(f[l][r],f[l][k]+f[k][r]+w[l]*w[k]*w[r]);
}
print(f[1][n]);
}
以上是关于[DP 区间 剖分 高精] 凸多边形划分的主要内容,如果未能解决你的问题,请参考以下文章