Java 求解二叉树的最小深度

Posted 2021-05-23 南淮北安

文章目录

• • 一、题目
  • 二、题目分析
  • 三、递归分析
  • 四、迭代分析
  • 五、总结

一、题目

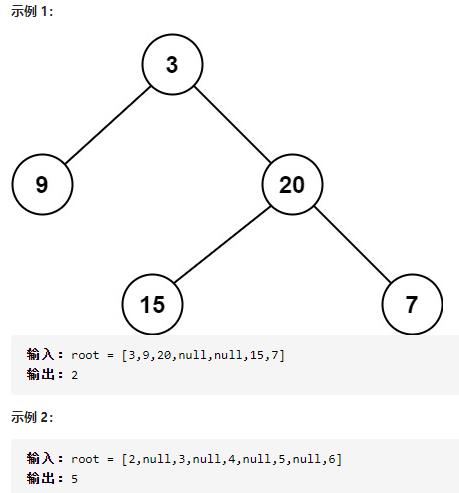
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

二、题目分析

该题乍一看和求解最大深度类似，但是区别还是很大的

遍历顺序是后序遍历（因为要比较递归返回之后的结果）

需要注意处理节点时：

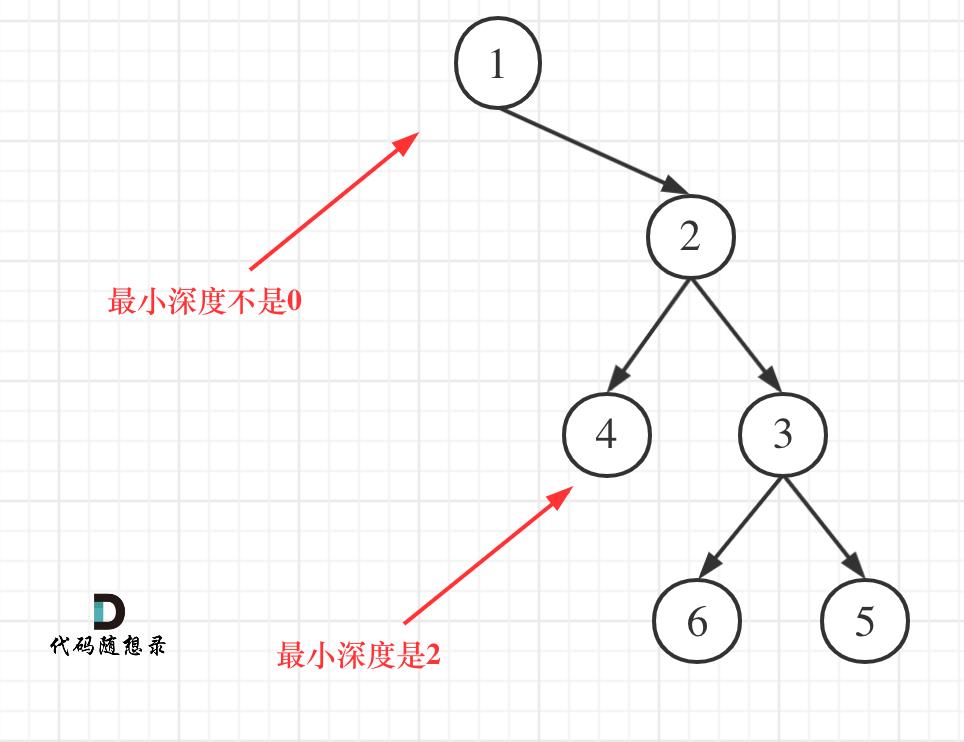
所以最小深度是从根到最近叶子节点的最短路径

叶子节点，左右孩子都为空的节点

三、递归分析

（1）确定递归函数的参数和返回值

参数即为二叉树节点，返回值即二叉树的深度

（2）确定递归终止条件

遇到空节点返回0，表示当前节点的高度为0

（3）确定单层递归的逻辑

叶子节点：左右节点均为空
所以，如果左子树不空，右子树为空，则说明最小深度是1+右子树的深度
所以，如果左子树为空，右子树不空，则说明最小深度是1+左子树的深度
所以，如果左右子树均不为空，则说明最小深度是左右子树最小值加1

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        //左子树为空，右子树不为空，最小深度为 1+右子树的深度
        if (root.left == null && root.right != null) {
            return rightDepth + 1;
        }
        //左子树不为空，右子树为空，最小深度为 1+左子树的深度
        if (root.left != null && root.right == null) {
            return leftDepth + 1;
        }
        //左右子树均不为空，最小深度为左右子树的最小长度加1
        return Math.min(leftDepth, rightDepth) + 1;
    }
}

四、迭代分析

利用层序遍历的思想：

import java.util.Deque;
import java.util.LinkedList;

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        //记录最小深度
        int res = 0;
        int size = 0;
        Deque<TreeNode> deque = new LinkedList<>();
        TreeNode node;
        deque.add(root);
        while (!deque.isEmpty()) {
            size = deque.size();
            res++;
            while (size > 0) {
                size--;
                node = deque.poll();
                if (node.left != null) {
                    deque.add(node.left);
                }
                if (node.right != null) {
                    deque.add(node.right);
                }
                //当左右子树均为空时，到达叶子节点
                if (node.left == null && node.right == null) {
                    return res;
                }
            }
        }
        return res;
    }
}

五、总结

最大深度：左右子树的最大值加1

最小深度，需要注意是根节点到叶子节点的距离，需要分情况讨论：

如果左子树不空，右子树为空，则说明最小深度是1+右子树的深度
如果左子树为空，右子树不空，则说明最小深度是1+左子树的深度
如果左右子树均不为空，则说明最小深度是左右子树最小值加1