学习笔记之——视觉里程计之各种几何映射
Posted gwpscut
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了学习笔记之——视觉里程计之各种几何映射相关的知识,希望对你有一定的参考价值。
之前博客《ROS实验笔记之——基于stereo camera的视觉里程计的实现》实现了基于双目相机的视觉里程计,而博客《学习笔记之——P3P与ICP位姿估计算法及实验》也介绍了一些基本的概念。本博文再次介绍一下其相关的一些基本知识及概念。本博文部分内容来自于网络参考,本博文仅仅是本人学习记录用,不做任何商业用途~
在视觉里程计中,特征点法是非常重要的,在视觉SLAM中,可利用图像的特征点作为SLAM中的路标。在经典的SLAM模型中,以路标(landmark)来描述SLAM过程。所谓的landmark是三维空间中固定不变的点,能够在特定位姿下观测到。而关于特征点的提取以及光流法等等,在之前的博客中也都以及介绍过了(《学习笔记之——vs2015+opencv2.4.13实现SIFT、SURF、ORB》、《学习笔记之——ORB-SLAM1、2、3》)
通过特征匹配,我们可以得到特征点之间的对应关系。分为下面三种情况:
- 只有两个单目图像,得到的是2D-2D间的关系,也就是对极几何;
- 若匹配到的是帧和地图,那么可以得到3D-2D的关系,也就是pnp
- 如果匹配的是点云(RGB-D),得到3D-3D的关系,ICP
目录
对极几何约束(2D-2D)
对极几何研究的是两张图像之间的关系。对于特征匹配得到的一对配对好的特征点,从而恢复出两帧之间相机的运动(也就是视觉里程计啦~)那到底需要多少对呢?答案是4对,8个点。
如下图所示(经过特征匹配后,知道p0和怕是同一个点)。它表示的是一个运动的相机在两个不同位置的成像,其中:左右两个平行四边形分别是相机在不同位置的成像平面。C0, C1分别是两个位置中相机的光心,也就是针孔相机模型中的针孔。P是空间中的一个三维点,p0, p1分别是P点在不同成像平面上对应的像素点。
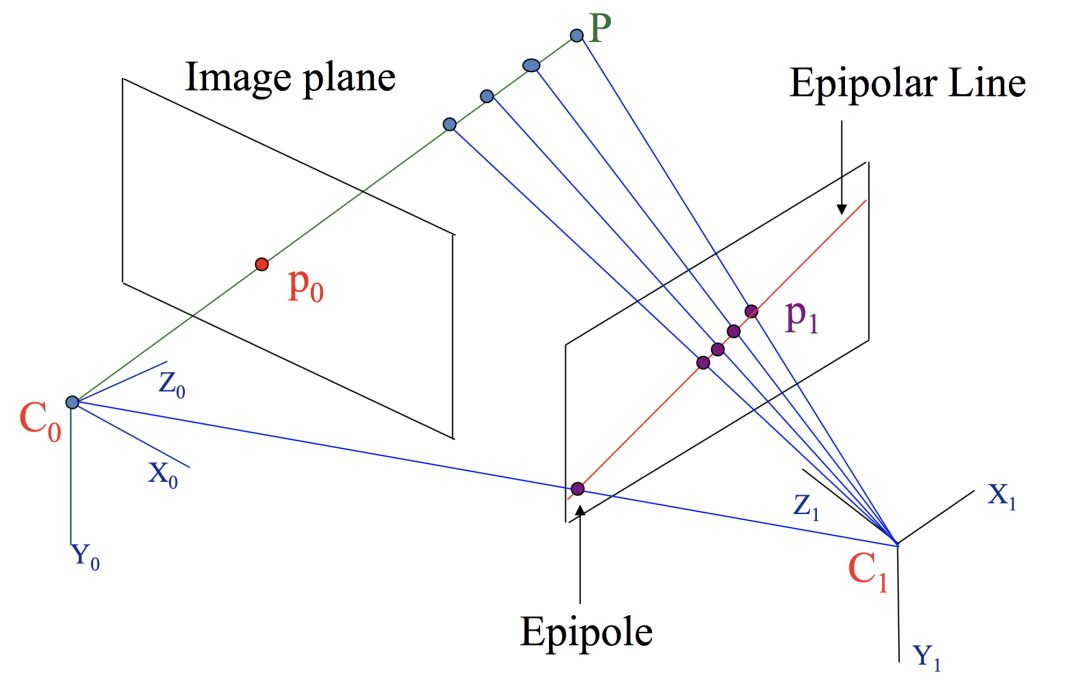
其中,C0-C1-P组成的平面称之为极平面(epipolar plane),其中和成像平面相交的直线称之为极线(epipolar line),两个光心C0, C1和成像平面的交点叫做极点(epipole)。看上面左侧的图,如果将点P沿着C0-p0所在的直线移动,你会发现P在左边相机的成像一直不变,都是p0,这时候P在右边相机的成像点p1是一直在变化的。
把极平面中C0-C1-p0-p1单拎出来,看下面的图:
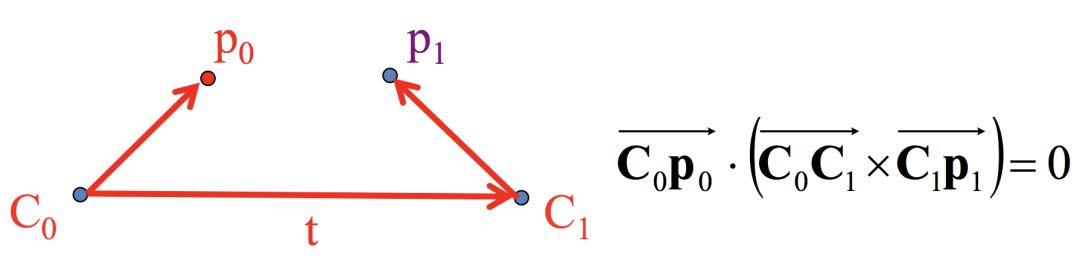
p0在以C0为原点的参考坐标系,p1在以C1为原点的参考坐标系,所以我们还是需要转换坐标系。这里我们把所有点的坐标都转换到以C0为原点的坐标系。前面说过这些向量都是方向向量和向量起始位置无关,所以这里坐标系变换只考虑旋转就可以。我们记 R 为从C1坐标系到C0坐标系的旋转矩阵。那么 Rp1 就是p1 在以C0为原点的C0坐标系了。
对于上式,根据叉乘的定义![]() 的结果是一个同时垂直于它们的向量,也就是说垂直于C0-C1-p0-p1组成的极平面,因此这个叉乘的结果再点乘
的结果是一个同时垂直于它们的向量,也就是说垂直于C0-C1-p0-p1组成的极平面,因此这个叉乘的结果再点乘![]() 结果就是0了。
结果就是0了。
最左边向量C0-p0就可以用p0表示,向量C0-C1就是光心C1相对于C0的平移,我们记为t, 向量C1-p1根据前面的讨论,可以用 Rp1 来表示,那么结论1可以表示为以下的结论2:
![]()
这个式子是根据对极几何得到的,我们称之为对极约束。一般把中间的部分拿出来,像下面这样,记为本质矩阵或本征矩阵(Essential Matrix)。
![]()
然后我们就得到了如下的结论3:
![]()
本质矩阵(Essential Matrix)
本质矩阵E = t^R。它是一个3 X 3 的矩阵,内有9 个未知数。
• 本质矩阵是由对极约束定义的。由于对极约束是等式为零的约束,所以对E 乘以任意非零常数后,对极约束依然满足。我们把这件事情称为E 在不同尺度下是等价的。
• 根据E = t^R,可以证明,本质矩阵E 的奇异值必定是![]() 的形式。这称为本质矩阵的内在性质。
的形式。这称为本质矩阵的内在性质。
• 另一方面,由于平移和旋转各有三个自由度,故t^R 共有六个自由度。但由于尺度等价性,故E 实际上有五个自由度。
E具有五个自由度的事实,表明我们最少可以用五对点来求解E。但是,E 的内在性质是一种非线性性质,在求解线性方程时会带来麻烦,因此,也可以只考虑它的尺度等价性,使用八对点来估计E——这就是经典的八点法(Eight-point-algorithm)
八点法可以用于单目SLAM的初始化
单应性矩阵(homography matrix)
单应矩阵描述的就是同一个平面的点在不同图像之间的映射关系,这里前提是同一个平面,这个前提很重要。接下来先看单应矩阵应用的一个例子。比如现在支付宝,微信都能通过对银行卡拍照自动识别银行卡号码,但是一般我们拍照时银行卡都不一定是正对着相机,可能会比较偏,比如像这样

但是对着银行卡拍完照之后,会发现这些软件会自动把银行卡抠出来,并且校正成非常规则的矩形,像下面这样。识别银行卡数字的时候也方便多啦!

单应矩阵能够实现自动把银行卡从背景里“提取”出来,并且变成非常规整的矩形。这个银行卡是一个平面,所以满足“同一个平面的点”的要求,那不同图像就是指拍摄的原始图像和校正过的图像。单应矩阵还有几个很重要的应用,一个是相机标定,比如张正友相机标定法,如下图所示
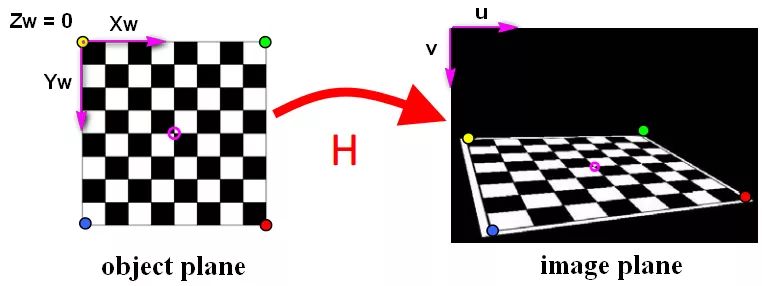
另外一个是单应矩阵还可以用于图像拼接,如下图所示。

利用平面二维标记图案(marker)来做AR展示的触发。根据单应矩阵就可以知道marker不同视角下的图像,这样可以方便的得到虚拟物体的位置姿态并进行显示,如下图所示。

如下图所示。两个不同的相机拍摄同一个平面
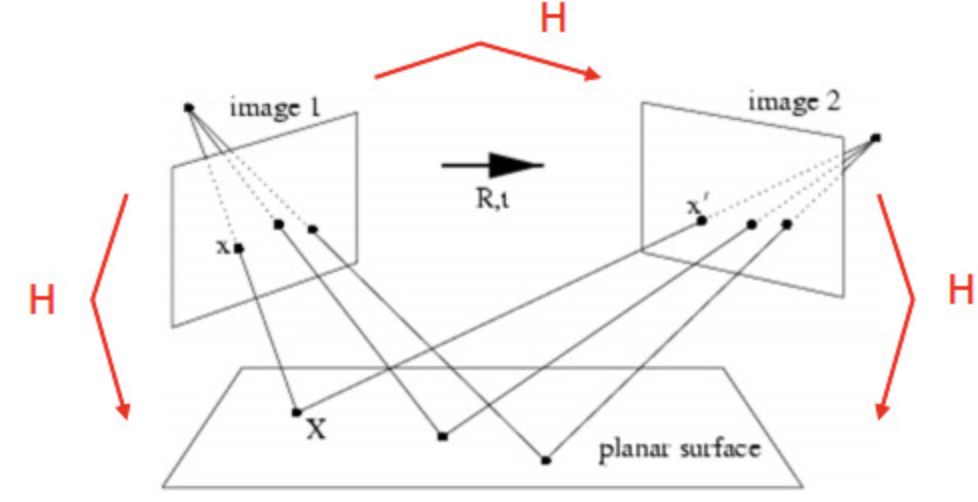
有世界坐标到像素坐标的转换公式如下:
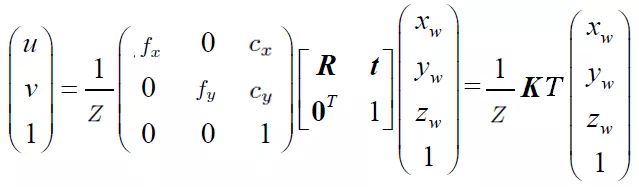
现在我们简化一下表达形式,把中间部分记做M矩阵,如下
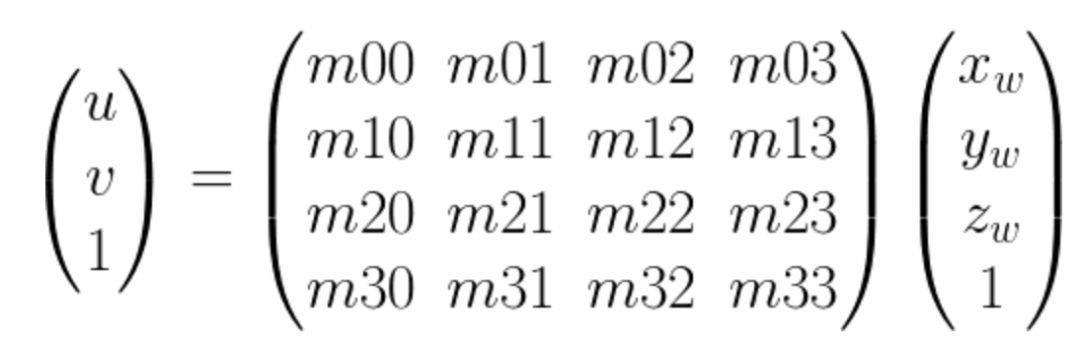
M矩阵是一个4 x 4 的矩阵,如果空间点在同一个平面上的话,我们可以看做 zw = 0,这样M矩阵就变成了一个 3 x 3的矩阵,对于两个不同的相机,像素坐标和空间点坐标可以写成如下的表示,其中M是3 x 3的矩阵
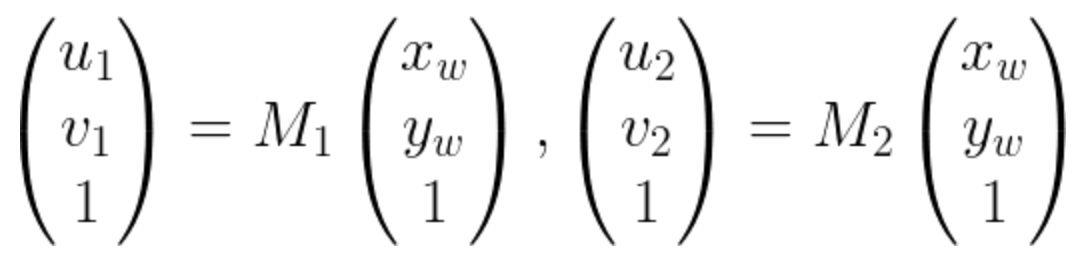
把上面两个式子合并一下就得到了下面这个式子,其中的H就是单应矩阵啦!H矩阵的两边是两张图像对应的匹配点对。也就是说单应矩阵H把三维空间中同一平面的点在两个相机的成像图片坐标进行了映射。
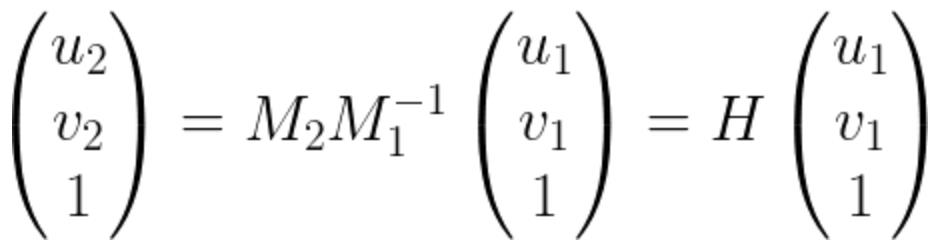
上面的式子就是两个图像上的匹配的点对的映射。,如果展开会发现一个式子对应2个方程。也就是两个约束项。而单应矩阵本身自由度为8(因为等式两边都是齐次坐标,所以可以进行任意尺度的缩放。因此一般都会对H进行归一化,比如把最后一个元素设置为1,或者使得H矩阵所有元素的二范数为1),所以只需要4个匹配点对就行啦。
对于2D-2D的情况,只知道图像坐标之间的对应关系:
- 当特征点在同一个平面上时(如俯视或仰视,比如之前的project基于marker的),可使用单应性矩阵来恢复R与t
- 否则,使用本质矩阵恢复R与t
求得R与t后,采用三角法来获得深度
PnP(3D-2D)
已知3D点的空间位置和相机的投影点,求相机的旋转和平移
- 代数方法(当对pose完全不知道的时候):P3P
- 优化方法(当有比较好的初始值的时候):Bundle Adjustment
前面提到过,对于2D-2D的对极几何问题,需要8个或以上的点对(八点法)。而如果两张图像中,其中一张的特征点的3D位置已知,那么至少需要3个点对(需要至少一个额外点验证结果)就可以估计相机的运动
p3p仅仅使用三对匹配点,对数据的要求较少
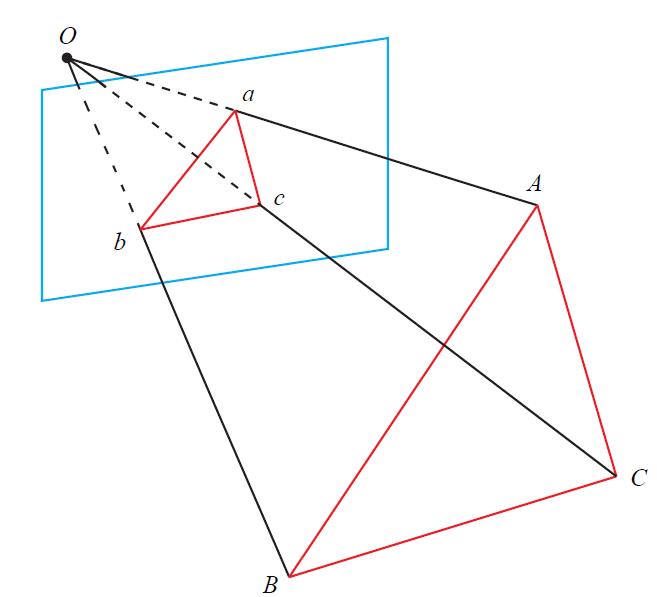
关于P3P的问题,之前博客《学习笔记之——P3P与ICP位姿估计算法及实验》已经介绍了过了,这里就不详细介绍了。
Bundle Adjustment
在SLAM 当中,通常的做法是先使用P3P/EPnP 等方法估计相机位姿,然后构建最小二乘优化问题对估计值进行调整(Bundle Adjustment,中文为光束法平差)。
在近几年兴起的基于图的SLAM算法里面使用了图优化替代了原来的滤波器,这里所谓的图优化其实也是指BA。
所谓的BA是指从视觉重建中提炼出最优的3D 模型和相机参数(内参数和外参数)。从每一个特征点反射出来的几束光线(bundles of light rays),在我们把相机姿态和特征点空间位置做出最优的调整(adjustment) 之后,最后收束到相机光心的这个过程。
这样描述有点抽象,简单的说,BA的本质是一个优化模型,其目的是最小化重投影误差。那么什么是重投影误差呢?如下图所示。上面的五颜六色的线就是前面讲的光束。那么什么叫重投影呢?
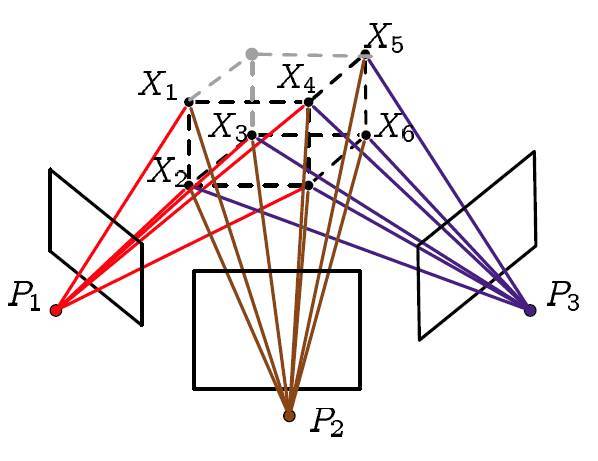
重投影也就是指的第二次投影,那到底是怎么投影的呢?我们来整理一下吧:
- 第一次投影指的就是相机在拍照的时候三维空间点投影到图像上
- 然后我们利用这些图像对一些特征点进行三角定位(triangulation,利用几何信息构建三角形来确定三维空间点的位置,相关内容请参考对极几何)
- 最后利用我们计算得到的三维点的坐标(注意不是真实的)和我们计算得到的相机矩阵(当然也不是真实的)进行第二次投影,也就是重投影
而所谓的重投影误差是指真实三维空间点在图像平面上的投影(也就是图像上的像素点)和重投影(其实是用我们的计算值得到的虚拟的像素点)的差值,因为种种原因计算得到的值和实际情况不会完全相符,也就是这个差值不可能恰好为0,此时也就需要将这些差值的和最小化获取最优的相机参数及三维空间点的坐标。
BA属于批量式的优化方法。给定很多个相机位姿与观测数据,计算最优的状态估计。定义每个运动、观测方程的误差,并从初始估计开始寻找梯度下降。
world frame下的三维坐标点与该点在图像平面的像素坐标转换如下所示:
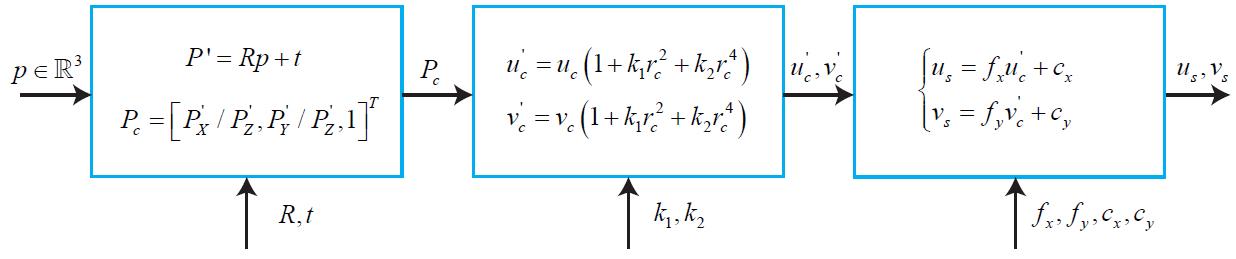
该过程即所谓的观测方程

对这个最小二乘进行求解,相当于对位姿和路标同时作了调整,也就是所谓的BA。
换个角度来讲,构建一个图优化模型。这个图模型的节点由相机Pi和三维空间点构成Xj构成,如果点Xj投影到相机Pi的图像上则将这两个节点连接起来。
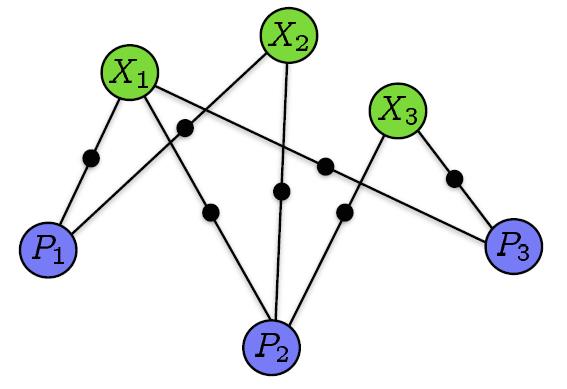

其中,式![]() 为BA优化模型的数学形式了。既然是优化模型,那自然就应该用各种优化算法来进行计算了。BA现在基本都是利用LM(Levenberg-Marquardt)算法并在此基础上利用BA模型的稀疏性质来进行计算的,LM算法是最速下降法(梯度下降法)和Gauss-Newton的结合体,之前博客《学习笔记之——非线性优化的解读》已经对各种非线性优化问题进行了解读。
为BA优化模型的数学形式了。既然是优化模型,那自然就应该用各种优化算法来进行计算了。BA现在基本都是利用LM(Levenberg-Marquardt)算法并在此基础上利用BA模型的稀疏性质来进行计算的,LM算法是最速下降法(梯度下降法)和Gauss-Newton的结合体,之前博客《学习笔记之——非线性优化的解读》已经对各种非线性优化问题进行了解读。
BA的稀疏性
最开始的时候,人们认为BA的计算量特别大,但是最近十年来,人们逐渐意识到SLAM问题中,BA的稀疏性,进而使得其在实时场景中使用。
ICP(3D-3D)
假设我们在三维空间中有两组点集,我们分别称之为P1, P2好了,P1, P2中都有几千个点,那么可以分为两种情况:
1、我们完全不知道P1, P2中每个点是如何对应的。这样的情况很常见,比如我用只有depth的深度相机或者激光雷达在两个不同的位置对着一只兔儿分别拍摄一张深度图并转化为点云图,但不知道哪个点和哪个点对应,但是我想把这两个点云“融合”(registration)在一起,变成一个更完整的兔儿。

2、我们已经知道P1, P2中哪个点对应的哪个点。比如使用RGB-D相机分别在两个不同位置拍摄一张 RGB彩色图 + 深度图,而且彩色图和深度图是对齐好的。因为有彩色图我们就可以做特征点匹配了,且每个特征点都对应一个深度图上的深度值,所以我们能够得到两组对应好的三维点。
为了方便,我们用一个二维的例子来说明吧,初始是两个不同角度下的笑脸(深红色和绿色),下面是红色笑脸如何通过ICP过程和绿色笑脸重合的:

再以点云配准为例进行说明。假设现在有两幅待配准的点云(比如上面的小兔子),ICP算法是这样配准两幅点云的:
ICP算法流程
-
首先对于一幅点云中的每个点,在另一幅点云中计算匹配点(最近点)
-
极小化匹配点间的匹配误差,计算位姿
-
然后将计算的位姿作用于点云
-
再重新计算匹配点
-
如此迭代,直到迭代次数达到阈值,或者极小化的能量函数变化量小于设定阈值
下面是用三维点云进行ICP的一个效果
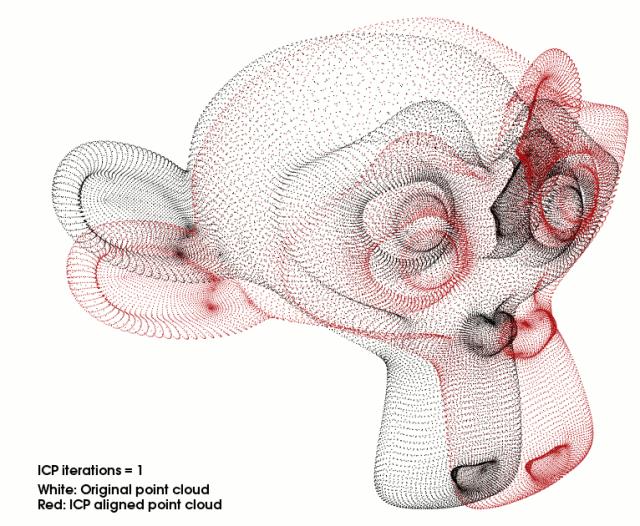
ICP的精髓其实就是迭代,一次次的修正错误,最后获得一个还不错的结果。不过话是这样说,但是一般情况下数据都有不少噪音,如果噪音较大,一般情况不一定能完全配准正确。
上面介绍是最简单的点和点匹配的ICP算法,实际应用中为了使得算法鲁棒,也就是在有不少噪声的情况下仍然能够得到正确的结果,很多研究者提出了不同的匹配思路:例如,极小化的误差项包括对应点的点到点的欧式距离,和对应点的点到平面距离,以及极小化对应点的颜色值误差等。
如果应用场景简单,数据干净基本没有噪声,最原始的点点匹配就行。如果有噪声,则最后考虑一下复杂点的方法。2003年的时候,pottman 和Hofer两位大牛的论文中证明了当两幅点云比较接近时,极小化对应点的点到平面距离比点到点距离更接近两个平面之间的真实距离,也就是说计算点到平面的距离更靠谱。下面是个示意图
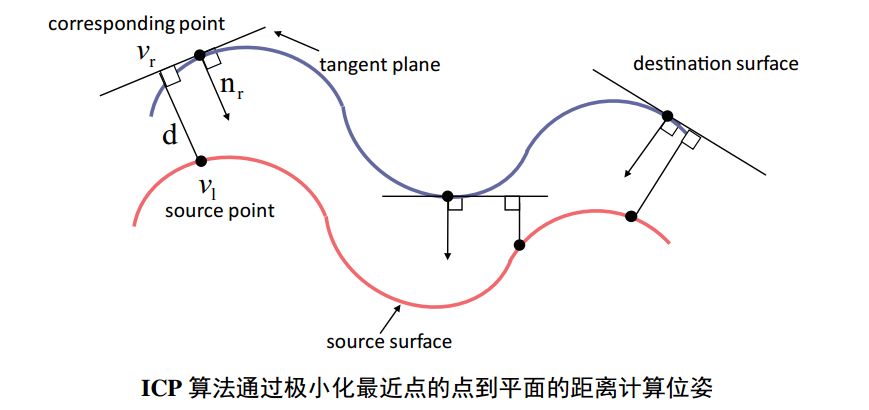
参考资料
《SLAM十四讲》
https://blog.csdn.net/OptSolution/article/details/64442962?utm_source=copy
https://mp.weixin.qq.com/s/aOhkY-Pj9O3wDim55_KY8w
https://mp.weixin.qq.com/s/bvezdrhfRRDp2CBBeKzUfw
https://mp.weixin.qq.com/s/8lbWNZB_rAq3W5YcrxVNHw
以上是关于学习笔记之——视觉里程计之各种几何映射的主要内容,如果未能解决你的问题,请参考以下文章